Page 18 - 《含能材料》优秀论文（2019年）

140 李萍，敖登高娃，李纯志，段晓惠，裴重华

表 1 常见固体热分解反应机理及其动力学方程 ［21］
Table 1 The thermal decomposition mechanism and kinetic
equations of common solids
reaction mechanism
number reaction mechanism
equation
1 1-a random nucleation，
a core for a particle
2 2（1-a） [ -ln(1 - a ] 1/2 random nucleation，
avrami‑erofeev equation，A 2
3 3（1-a） [ -ln(1 - a ] 2/3 random nucleation，
a. raw TATB avrami‑erofeev equation，A 3
4 2(1 - a ) 1/2 phase boundary reaction，
cylindrically symmetry
5 3-(1 - a ) 2/3 phase boundary reaction，
spherical symmetry
6 1/（2a）
one‑dimensional diffusion
7 [ -ln(1 - a ] -1 two‑dimensional diffusion，
cylindrically symmetry
8 1.5(1 - a ) 2/3 [1 - (1 - a ) 1/3 -1 three‑dimensional diffusion，
]
spherical symmetry，
b. keel‑liked TATB jander equation
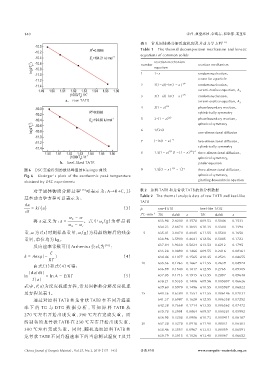
图 6 DSC 实验得到的放热峰温的 Kissinger 曲线 9 1.5［ (1 - a ) -1/3 - 1 ］ -1 three‑dimensional diffusion，
Fig. 6 Kissinger′s plots of the exothermic peak temperature spherical symmetry，
obtained by DSC experiments ginstling‑brounshtein equation
对于固体物质分解过程 ［19］ 可表示为：A→B+C，其 表 2 原料 TATB 和龙骨状 TATB 的热分析数据
Table 2 The thermal analysis data of raw TATB and keel‑like
基本动力学方程可以表示为： TATB
da = kf ( ) a
dt （3） β /℃·min -1 raw‑TATB keel‑like TATB
ω - ω T/K da/dt a T/K da/dt a
将 a 定 义 为 ：a = 0 。 式 中 ω（g）为 样 品 初 633.98 2.6200 0.3578 609.53 0.5046 0.1533
0
ω - ω i 634.23 2.6870 0.3655 610.35 0.5304 0.1594
0
重，ω 为 t（s）时刻样品重量，ω（g）为样品热解后的残余 5 635.41 3.0470 0.4045 611.55 0.5584 0.1658
i
重量，单位均为 kg。 636.96 3.5900 0.4641 612.56 0.5885 0.1723
反应速率常数可用 Arrhenius 公式为 ［20］ ： 637.84 3.9330 0.5024 613.53 0.6212 0.1795
E 633.28 0.0890 0.1466 609.55 0.2416 0.08361
k = Aexp( - ) （4） 634.46 0.1077 0.1565 610.35 0.2523 0.08655
RT
10 635.56 0.1263 0.1667 611.55 0.2639 0.08974
由式（3）和式（4）可得： 636.99 0.1540 0.1817 612.55 0.2765 0.09305
( da/ dt )
ln = ln A - E/RT （5） 637.85 0.1713 0.1915 613.55 0.2897 0.09648
f ( a ) 638.21 0.5335 0.1406 609.56 0.005807 0.06626
式中，f（a）为反应机理方程，常见固体热分解反应机理 639.60 0.5979 0.1496 610.55 0.005987 0.06822
及方程见表 1。 15 640.36 0.6380 0.1551 611.55 0.006146 0.07031
通过对原料 TATB 和龙骨状 TATB 在不同升温速 641.37 0.6987 0.1628 612.55 0.006358 0.07252
642.38 0.7668 0.1714 613.55 0.006562 0.07472
率 下 的 TG 与 DTG 数 据 分 析 ，可 知 原 料 TATB 从
635.78 0.2991 0.0864 609.57 0.000381 0.05992
270 ℃左右开始出现失重，390 ℃左右完成失重。而
636.95 0.3208 0.0906 610.73 0.000411 0.06187
所制备的龙骨状 TATB 在 230 ℃左右开始出现失重， 20 637.28 0.3278 0.0918 611.90 0.00031 0.06383
380 ℃左右完成失重。同时，随机选取原料 TATB 和 638.46 0.3552 0.0967 613.03 0.00059 0.06591
龙骨状 TATB 不同升温速率下的当前测试温度 T 及其 639.79 0.3915 0.1026 613.40 0.00067 0.06652

Chinese Journal of Energetic Materials，Vol.27, No.2, 2019（137-143） 含能材料 www.energetic-materials.org.cn