Page 74 - 《含能材料》2018年优秀论文

HTPB 推 进 剂 温 度 相 关 性 失 效 准 则 735

HTPB 推 进 剂 线 粘 弹 性 本 构 模 型 的 卷 积 分 形 式 （α 由第 3 节求出），可以得到应力‐折算时间曲线，但
T
如下 ［14］ ： 是仍不便带入式（10）中进行数值计算。为了方便计
t dε 算，在这里引入一种常用的应力-折算时间函数 ［19］ ：
σ = ∫ E ( ξ - ξ ) dτ （6）
t
τ
0 dτ M ξ
0
式中，E（t）为松弛模量，MPa；ξ 为折算时间，s；τ 为积分 σ( ξ ) = M ξ ξ （11）
变量。其中将松弛模量表示为 n 阶 Prony 级数形式， 1 + ( σ 0 - 2 ) ξ + ( ξ ) 2
对于等速拉伸过程，应变率保持不变， ε ̇ = dε/ dτ 则式 f f f -1
0
0
f
（6）变为： 式中，M 为应力时间曲线的初始斜率，MPa·s ；ξ 为材
料折算失效时间，s；σ 为临界失效应力，MPa。将温度
f
t é n ξ - ξ τ ù
t
σ = ε ̇ 0 ∫ ê êE + E exp ( - ú ) dτ 为 293.15 K 下拉伸速度为 0.5，2，100 mm·min 的
-1
ú
∞ ∑
i
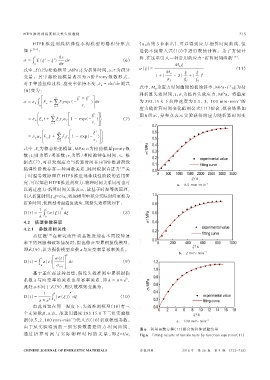
0 ë i = 1 τ i û 应力随折算时间变化值用公式（11）拟合，拟合结果如
{ n é ξ t ù } 图 6 所示，分布点表示实验获得的应力随折算时间变
= ε ̇ 0 E t + ∑ E τ α ê1 - exp( - ú ) ú （7）
T ê
i
∞
i
i = 1 ë τ i û
{ n é ξ t ù }
= ε ̇ α T E ξ + ∑ E τ ê1 - exp( - ú ) ú
i ê
0
i
∞
i = 1 ë τ i û
式中，E 为稳态松弛模量，MPa；n 为松弛模量 prony 级
∞
数；E 则为第 i 项系数；τ 为第 i 项松弛特征时间，s。根
i
i
据式（7），可以发现应力与折算时间在 HTPB 推进剂线
粘弹性阶段存在一种函数关系，同时根据许进升 ［17］ 关
于时温等效原理在 HTPB 推进剂非线性阶段的适用研
究，可以知道 HTPB 推进剂应力‐物理时间关系同时也可 a. 0.5 mm·min -1
以通过应力‐折算时间关系表示，故基于时温等效原理，
引入折算时间 ξ，ξ=t/α ，将原模型中积分实际时间更换为
T
折算时间，使模型考虑温度效应，则新失效准则如下：
1 ξ β
D ( t ) = ∫ ( σ( ξ ) ) dξ （8）
λ 0
4.2 模型参数获取
4.2.1 参数率相关性
孟红磊 ［18］ 在研究改性双基推进剂在不同拉伸速
率下的屈服和破坏情况时，提出修正型累积损伤模型，
即式（9），认为损伤模型参数 a 与应变率呈幂率关系。
b. 2 mm·min -1
β
t é σ( t ) ù
D ( t ) = ∫ a( ε ̇ ) ê ê ú dt （9）
ú
0 ë σ ref û
基于孟红磊这种思想，假设失效准则中累积损伤
b
系数 λ 与应变率的关系也呈幂率关系，即 λ = a × ε ̇ ，
此处 a 不同于式（9），则失效准则变换为：
1 ξ β
D ( t ) = b ∫ ( σ( ξ ) ) dξ （10）
a × ε ̇ 0
由此可知在同一温度下，失效准则模型（10）有三
个未知数 β，a，b。故选用温度 293.15 K 下三组实验数
-1
据（0.5，2，100 mm·min ）代入式（10）求取模型参数。 c. 100 mm·min -1
由于从实验得到的三组实验数据是应力‐时间曲线，
图 6 利用函数方程（11）拟合的拉伸试验结果
通过 折 算 时 间 与 实 际 物 理 时 间 的 关 系 ，即 ξ=t/α T Fig.6 Fitting results of tensile tests by function equation（11）

含能材料 2018 年 第 26 卷 第 9 期 （732-738）
CHINESE JOURNAL OF ENERGETIC MATERIALS