同轴内外层双元组合装药是一种工程中常见的装药方式, 早期主要是采用不敏感炸药包覆高能炸药以提高整体装药对各类危险刺激的不敏感性^[1-2]。近年来, 国内外一些研究人员尝试采用该结构调节装药的能量释放特性^[3], 并通过相关的战斗部工程试验进行了验证。如, Arthur Spencer等^[4]、尹俊婷等^[5]将高爆速炸药包裹高爆热炸药的同轴双元组合装药应用于杀爆战斗部中, 以兼顾破片速度和冲击波超压两方面的性能; 牛余雷等^[6]研究了类似双元组合装药在不同介质中的爆炸冲击波超压变化规律。但这些研究主要偏重于爆炸作用效果方面, 对于爆轰过程中内外层装药的相互影响以及整体装药结构的能量输出过程方面的深入研究还较少。

由于同轴双元装药中的两种炸药一般存在一定的爆速差, 从而使内外层装药间的爆轰波出现耦合现象, 这可能会改变两种炸药固有的爆轰反应区宽度及能量释放特性, 尤其非理想炸药, 还需考虑铝粉的反应速率是否改变。Manfred Held^[7]曾利用端面波形扫描法获取了该类装药几种典型结构的爆轰波形, 发现这些波形整体上呈现明显的聚心或散心特征, 其中爆速低的炸药会发生一定程度的超压爆轰, 但并未进一步分析其对作功能力的影响。周涛等^[8]利用两种含铝量分别为5%和20%的3, 4-二硝基呋咱基氧化呋咱(DNTF)基炸药制备了两种典型的同轴双元组合装药, 并采用圆筒试验对比了两种组合装药的驱动释能过程, 发现外层使用高爆速炸药时, 组合装药的驱动能力相对较强, 尤其在加速阶段后期, 圆筒壁仍存在明显的加速度; 同时, 还对比了该组合装药与含铝量为5%的DNTF基炸药单一装药的驱动能力, 但由于该组合装药的平均含铝量为12.5%, 其总能量与含铝量为5%的单一装药有明显差别, 因此, 两者驱动能力的差异并不能反映组合装药结构对爆轰能量释放规律的影响。鉴于此, 本研究制备了一种含铝量为12.5%的DNTF基炸药单一装药, 并与该组合装药对比了圆筒试验结果, 通过结合该组合装药的爆轰波形扫描试验, 以期望能够更为详细、深入地分析这种外层为高爆速炸药的同轴双元组合装药的驱动释能特性, 为该装药的优化设计提供技术支撑。

实验样品制备时涉及的三种熔铸类炸药(DOL-1、DOL-2、DOL-3), 其组分及性能数据见表 1。待测样品包括由DOL-2炸药制备的单一装药以及由DOL-1和DOL-3两种炸药制备的组合装药, 两种装药均为圆柱形, 每节药柱的尺寸均为Φ50 mm×100 mm。其中, 组合装药为同轴内外层组合圆柱体, 外层为爆速较高的DOL-1炸药, 内层则为爆速相对较低的DOL-3炸药, 且其直径为35 mm, 内外层装药质量相同, 平均密度为1.87 g·cm^-3。表 1显示, 该组合装药各组分的平均比例与DOL-2基本相当。

表 1(Tab. 1)

表 1 炸药试样配方及参数 Tab. 1 Formulation andparameters of explosive samples explosive ω/% ρ/g·cm-3 DCJ/mm·μs-1 DNTF HMX Al binder DOL-1 30 60 5 5 1.84 8.65 DOL-2 30 52.5 12.5 5 1.87 8.49 DOL-3 30 45 20 5 1.90 8.21 Note: ω is the mass ratio. ρ is the density. DCJ is the detonation velocity at Chapman-Jouguet (CJ) state.

表 1 炸药试样配方及参数 Tab.1 Formulation andparameters of explosive samples

组合装药爆轰过程中, 其波形演变至稳态需要较长的距离, 这不仅与两种炸药的爆速差有关, 还受结构尺寸等因素的影响, 因此, 本试验中主要是分析特定长径比组合装药的波形特征。试验所用炸药均为金属加速型炸药, 鉴于很多杀伤战斗部装药的长径比近似为2, 故在试验中选用一节Φ50 mm×100 mm的药柱作为试验主装药, 并通过SJZ-15型转镜式高速扫描相机获得药柱尾部端面的爆轰波形, 实验布局如图 1所示。为了尽可能地反映组合装药爆轰波形的演变过程, 在待测药柱的起爆端粘接一个Φ50 mm的平面透镜, 以使得内外层装药的起始波形相同。同时, 将待测装药固定于木制支架的“V”形槽内, 以减小边界约束条件对爆轰波形的影响。扫描爆轰波形时, 相机的光学狭缝通过高清晰反射镜对准主装药柱端面的直径, 相机转速设定为12×10⁴ r·min^-1, 其对应的扫描速度为6 mm·μs^-1。为了提高相机底片的空间分辨率, 获得清晰的爆轰波形, 将1 mm厚的有机玻璃光探板与待测装药的测量端面粘贴, 预留约0.1 mm间隙, 当冲击波进入空气隙时, 隙中空气电离发出强光, 且冲击波离开光探板后, 阻止后续爆轰产物光线进入镜头, 起到爆炸快门的作用。

图 1(Fig. 1)

图 1 爆轰波形扫描实验装置示意图 Fig.1 Schematic diagram of scanning test device for detonation wave-shape

图 2为组合装药爆轰波形扫描试验底片, 结合图像放大比及相机的扫描速度可获得其曲线数值, 由于该曲线反映了爆轰波通过装药直径处的波形, 且沿装药轴向的对称性较好, 因此, 可仅显示沿装药半径R的波形曲线, 如图 3所示, 其中, t表示各点的相对时刻值。从图 3可以看出, 虽然装药整体波形呈内聚特征, 但由于内外层装药的爆速差仅约0.4 mm·μs^-1, 导致波形的演变速率偏慢, 爆轰波传至装药末端时, 中心部位仍有约Φ7 mm的平面波形区域; 同时, 外层装药的边侧区域受到侧向稀疏波的影响, 局部呈现散心特征。因此, 可依据爆轰波形的特征将装药分为三个部分。第一部分为中心的平面波形区域, 即R≤3.5 mm区域, 其爆轰波未受到侧向干扰, 法向爆速D_i仍沿装药轴向, D_i=8.21 mm·μs^-1, 由此结合图 3中各点的相对时刻值t及装药的总长度计算得出法向爆速D_n在装药轴向上的分量D_a, 具体曲线如图 4所示。第二部分为外层装药区域, 即17.5 mm<R≤25 mm区域, 该区域外侧受到空气侧向稀疏波影响, 内侧受到阻抗偏低的内层装药的影响, 波形呈散心特征, 曲率κ>0, 其拐点位于R≈21.7mm, 该处法向爆速D_e与装药轴向平行, 其数值为8.52 mm·μs^-1, 小于DOL-1炸药的稳态爆速, 此外, 该区域的波形关于拐点并不对称。第三部分为内层装药中的3.5 mm<R≤17.5 mm区域, 该区域波形主要受外侧装药影响而产生了不同程度的超压爆轰, 其法向爆速D_n略向装药中心处汇聚(波形曲率κ<0), 其数值介于D_i与D_e, 但由于图 3中的波形并非稳态波形, 目前也没有相关的拟合函数能够准确地描述组合装药的波形曲线, 因此, 难以准确计算出其法向爆速的具体值。

图 2(Fig. 2)

图 2 组合装药爆轰波形扫描底片 Fig.2 Scanning photograph of detonation wave shape of composite charge

图 3(Fig. 3)

图 3 组合装药爆轰波形曲线 Fig.3 Curve of detonation wave shape of composite charge

图 4(Fig. 4)

图 4 组合装药波形区域划分示意图 Fig.4 Schematic diagram of divided areas based on wave shape of composite charge

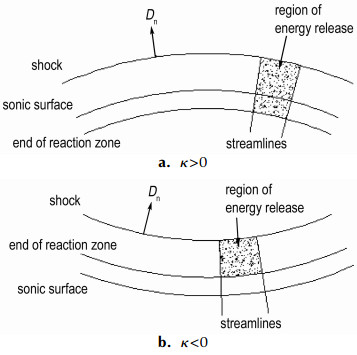
爆轰波形对于爆轰反应区能量的释放具有重要影响^[9-10]。对于外层装药的散心爆轰波(κ>0), 其声速面不再是化学反应平衡点, 如图 5a所示, 在声速面之后还有化学反应的能量释放, 虽然这部分能量不能贡献于爆轰波的传播, 但对于爆轰产物作功仍是有效的^[10]; 而对于内层装药的聚心爆轰波(κ<0), 在声速面之前化学反应就已经结束, 如图 5b所示，其高压环境对于含铝炸药中铝粉及爆轰产物的进一步反应可能是有益的。此外, 从整体装药的波形上看, 其内聚趋势对于内外层装药中爆轰产物及铝粉的进一步均匀混合也是有利的, 当然这还需要其它试验进一步研究。

图 5(Fig. 5)

图 5 散心和聚心波形条件下反应区示意图[9] Fig.5 Schematic diagram of reaction zone under the diverging/converging wave shape conditions[9]

虽然该组合装药的爆轰波形使内外层装药的爆轰反应区宽度均会发生变化, 但整体能量释放规律的变化还需要结合圆筒试验进一步分析。

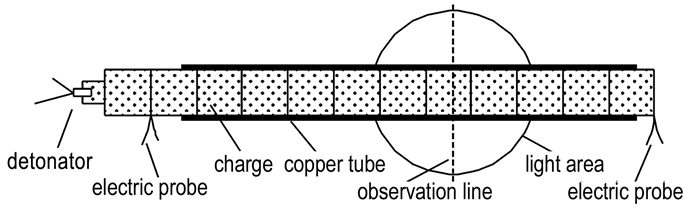
圆筒试验装置由待测主装药、传爆药柱、铜管、电探针、氩气弹、反射镜、GSJ高速转镜相机、高压雷管等组成, 如图 6所示。其中, 铜管的材料为TU1无氧铜, 密度为8.93 g·cm^-3, 内、外直径分别为50 mm和60.2 mm; 狭缝扫描位置距圆筒尾端约200 mm, 相机扫描速度设定为1.5 mm·μs^-1; 采用氩气弹作为照明装置; 通过固定于圆筒两端的电探针测定炸药的爆速, 对于组合装药, 则采用两组探针分别测量内、外层装药的爆速, 其中, 内层装药的探针粘贴于装药截面的中心, 外层装药的探针粘贴于R≈21.7 mm处, 以便于与图 4中的D_i和D_e进行对比。

图 6(Fig. 6)

图 6 圆筒试验装置示意图 Fig.6 Schematic diagram of the cylinder test device

组合装药的探针测量显示装药尾端的内外层探针导通时间间隔为0.4 μs, 而图 3中显示爆轰波到达这两处的时间间隔为0.44 ms, 两者较为接近。但圆筒中各层装药的爆速发生了明显变化, 如外层装药R≈21.7 mm处的爆速为8.626 mm·μs^-1, 而在图 4中, 该位置的爆速仅为8.52 mm·μs^-1, 这主要是因为圆筒壁向装药中反射的冲击波一定程度上提升了外层装药的爆速; 此外, 内层装药中心处的爆速也由图 4中8.21 mm·μs^-1增至8.612 mm·μs^-1, 这是由于圆筒试验中的装药较长, 随着爆轰波的逐渐演变, 内层装药中心处也受到影响, 其爆速得到了提升。

图 7为实验所获得的典型扫描底片, 通过对底片进行数字化处理, 得出圆筒壁外表面的膨胀距离Δr_e随时间变化的系列数据, 然后采用文献[11]中的方法, 假定圆筒壁膨胀过程中, 其横截面积保持不变, 并设定一个圆筒壁质量中心面, 其半径为r_m, 则存在以下关系。

图 7(Fig. 7)

图 7 圆筒壁膨胀的扫描照片 Fig.7 Scanning photograph of expansion process of the cylinder wall

式中, α为常数, mm²; r_i和r_e分别为圆筒壁的内、外半径, mm, r_i0和r_e0分别为两者的初始值。由公式(1)可知r_m的初始值${r_{{\rm{m0}}}} = {\rm{ }}\sqrt {(r_{{\rm{e0}}}^2 + r_{{\rm{i0}}}^2)/2} $, 并推导出公式(2), 可将圆筒壁外表面的(r_e-r_e0)-t数据转换为(r_m-r_m0)-t,

按照公式(3)对试验数据进行拟合,

式中, a_j、b_j均为拟合参数, t₀作为时间项的修正参数, 当t+t₀=0时, 圆筒壁的质量中心面开始膨胀。试验曲线拟合参数的具体值列于表 2中。

表 2(Tab. 2)

表 2 圆筒壁膨胀位移曲线拟合参数 Tab. 2 Curve-fitting parameters of the expansion displacement of the cylinder wall sample a1/mm·μs-1 b1/μs-1 a2/mm·μs-1 b2/μs-1 t0/μs composite charge 1.08976 0.11794 0.79153 0.51665 1.15438 DOL-2 1.12520 0.15351 0.75196 0.31026 0.91290

表 2 圆筒壁膨胀位移曲线拟合参数 Tab.2 Curve-fitting parameters of the expansion displacement of the cylinder wall

将公式(3)对时间求导, 可得到圆筒壁质量中心面的径向速度u_m的表达式

再进一步计算出圆筒质量中心面的质点速度u_s,

式中, D为炸药在圆筒内的爆速。由此可计算出圆筒的比动能,

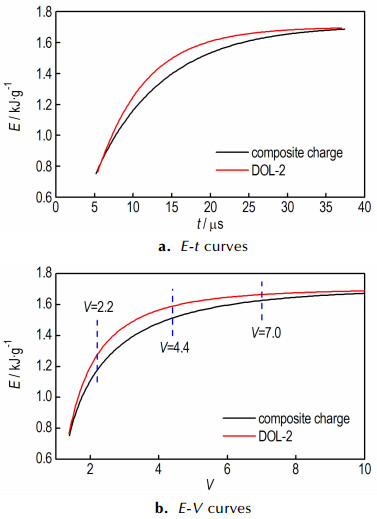
图 8为比动能随时间及爆轰产物相对比容V的变化曲线, 其中, V=(r_i/r_i0)²。图 8显示, 无论基于同一反应时间还是产物膨胀体积, 该组合装药的能量释放速率均低于DOL-2单一装药, 主要是圆筒膨胀初期的比动能差距较大, 后续逐渐缩小, 到圆筒膨胀末期时, 两者的比动能较为接近。依据爆轰产物特定相对比容处的比动能数据可以进行更为详细的对比(如表 3所示)。对于非理想炸药, V=2.2, 4.4, 7.0时可以反映爆轰产物的高压、中压、低压作用阶段的特征, 甚至V=10时还可以进一步反映铝粉的后续反应是否还能贡献金属的驱动。据表 3中可以算出, V=2.2时, 组合装药的圆筒比动能较DOL-2单一装药低8.1%, V=4.4及7.0时, 这一差距逐步缩小为4.7%及2.3%, 这是对金属驱动作功的主要阶段; 而V=10.0时, 这一差距则不足1%, 表明这两种装药的总能量相当。这也反映出虽然组合装药的爆轰波形一定程度上改变了炸药的爆轰反应区, 但并未明显减少总能量; 此外, 还反映出该组合装药虽然反应前期能量释放速率相对偏低, 但爆轰波的内聚趋势能促使内外层装药的爆轰产物能够迅速混合, 保证了铝粉有效释能。但在实际应用中, 对战斗部破片的有效驱动主要在爆轰产物的高、中压阶段, 因此, 在这一方面DOL-2单一装药较该组合装药具有一定的优势。

图 8(Fig. 8)

图 8 圆筒壁比动能变化曲线 Fig.8 The curves of change in specific kinetic energy for the cylinder wall

表 3(Tab. 3)

表 3 特定相对比容处的比动能 Tab. 3 Specific kinetic energy at given relative volumes kJ·g-1 sample V 2.2 4.4 7.0 10.0 composite charge 1.173 1.515 1.626 1.672 DOL-2 1.276 1.590 1.664 1.687

表 3 特定相对比容处的比动能 Tab.3 Specific kinetic energy at given relative volumes

圆筒壁的膨胀速度或比动能的变化属于驱动能量的积累效应, 为了更进一步对比两种装药的能量释放过程, 还可分析爆轰产物压力随相对比容的变化关系, 即爆轰产物p-V曲线, 该曲线是分析炸药爆轰产物作功特性的重要数据, 且基于此才能获得产物的状态方程参数。由于无氧铜具有较好的延展性, 一般V>10以后壳体才会完全破裂, 因此, 可获得较为完整的p-V曲线。这里首先采用文献[12]中的圆筒膨胀动力学模型, 以获得爆轰产物压力与圆筒的径向膨胀位移、材料的动态屈服强度之间的关系,

式中, ρ表示无氧铜的密度, 8.93 g·cm^-3; σ_ds为无氧铜的动态屈服强度, 175 MPa^[13]。然后结合公式(3)和(4), 则可获得p-t曲线, 再由爆轰产物相对比容的计算式可获得V-t曲线, 从而最终获得爆轰产物的p-V曲线。

图 9列出了组合装药与DOL-2单一装药p-V曲线的对比。从图 9可以看出, 在爆轰产物膨胀早期, DOL-2单一装药爆轰产物的压力高于该组合装药, 但随着爆轰产物相对比容的增大, 这一差距逐渐缩小, 最后低于组合装药, 这两条曲线的交叉点位于V≈2.69, 此时爆轰产物的压力为0.88 GPa。对于一般杀爆战斗部而言, 这一时刻处于壳体/破片加速阶段^[14], 这也意味着, 在相同战斗部中, 当壳体破裂后, 爆轰产物作用于空气产生冲击波时, 该组合装药的冲击波超压将会高于DOL-2单一装药。

图 9(Fig. 9)

图 9 爆轰产物p-V关系曲线 Fig.9 The p-V relation curves of detonation products

(1) 对于外层采用高爆速炸药的同轴双元组合装药, 其爆轰波形整体上具有内聚趋势, 但内外层装药的波形特征并不相同, 内层装药的波形曲率小于零, 外层装药的波形曲率大于零。

(2) 相比于各组分比例与组合装药一致的单一装药, 在爆轰产物膨胀初期, 该组合装药的圆筒比动能相对偏低, 产物相对比容为2.2时, 约偏低8.1%;随着爆轰产物的膨胀, 这一差距逐渐缩小, 产物相对比容为4.4及7.0时, 这一差距逐步缩小为4.7%及2.3%。

(3) 在产物膨胀早期, 该组合装药爆轰产物的压力偏低, 但产物相对比容增至2.69时, 便赶上了单一装药, 随后一直保持一定的优势。由此可以发现, 在战斗部应用中, 该组合装药能够在适当降低金属驱动能量的前提下有效提升冲击波能。