2. 中国工程物理研究院研究生部, 四川 绵阳 621999
2. Graduatedepartment, China Academy of Engineering Physics, Mianyang 621999, China
高聚物粘结炸药(polymer-bonded explosive, PBX)是一类广泛应用于武器工业领域的含能颗粒复合材料, 采用造型粉颗粒进行压制成型是其制造过程中的一个重要工序。成型密度直接影响着PBX炸药的力学、爆轰及安全性能[1-2], 一直以来备受关注, 工艺参数是影响PBX炸药密度的关键[3-4], 如何依据造型粉颗粒自身特性和期望密度科学地确定成型工艺已发展成为一个重要的制造工艺方向。随着高能钝感绿色弹药需求的提升, 含能材料科学突飞猛进, 炸药新配方不断涌现, 工艺参数确定的高效经济需求与传统工艺试验的费时费力现状间的矛盾越来越突出, 研究造型粉致密化成型中的密度演化规律对于最终实现造型粉颗粒的可压性评价和成型工艺参数的科学预测具有重要意义。
从力学的观点来看, 压制成型的过程本质上是输入载荷、温度和时间等参数, 造型粉颗粒聚集体在松装密度的基础上密度不断演化直至最终成型的过程。依据具体的工艺环节, 可将造型粉的致密化成型过程分为加载、卸载和回复三个阶段, 若能分别描述出三个阶段中成型密度的演化规律并函数化, 势必能够最终建立一个密度演化模型, 进而实现工艺参数输入与期望密度输出间的双向预测计算。谭武军等[5]采用Kawakita方程[6]和Heckel方程[7]对黑索今(RDX)和奥克托今(HMX)晶体的压制曲线进行了拟合, 比较了两个压制方程的描述精度, 得到了Kawakita方程可用于描述炸药晶体压制曲线的结论; 李明等[8]根据含能晶体的压制曲线定义了晶体颗粒聚合体的初始割线模量, 并据此评价了含能晶体颗粒的凝聚强度; 目前关于造型粉成型工艺参数对密度影响的研究工作[3-4]还主要集中于定性描述的阶段, 尚未探讨过二者之间的定量关系, 前述以炸药晶体为研究对象的工作[5-6]为针对造型粉开展成型密度演化规律的研究提供了方法指导和思想支撑。
本研究以两种PBX造型粉为研究对象, 参考陶瓷冶金等领域的研究成果[6-7, 9-11], 基于对各自加载过程中的密度演化特性分析的结果采用Kawakita方程[6]和Gerdemann-Jablonski方程[11]尝试建立加载曲线方程, 以期为掌握造型粉致密化中的密度演化规律, 实现造型粉颗粒的可压性评价和成型工艺预测奠定基础。
2 实验部分 2.1 实验样品与仪器研究中的两种TATB基PBX造型粉(PBX-A和PBX-B), 炸药晶体的质量分数均大于93%, 由中国工程物理研究院化工材料研究所提供, 常温常压下理论最大密度均为1.942 g·cm-3, 其中PBX-B在PBX-A组分基础上添加了微量改性添加剂, 粒径分布范围较PBX-A造型粉更大。
试验在INSTRON 5582型材料试验机上进行, 加载工装如图 1所示(工装内径d为19.96mm), 称量采用Mettler Toledo XS204型精密天平。
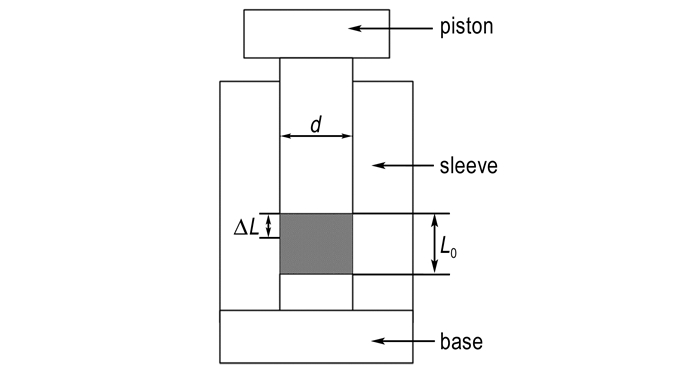
|
图 1 模具示意图 Fig.1 Schematic diagram of die |
试验在常温下进行, 加载过程中材料试验机的横梁速率为0.5 mm·min-1, 最大加载载荷包括40, 60 kN和80 kN三种, 分别对应造型粉在模具中受到压力127, 191 MPa和255 MPa, 每个工况重复试验三次, 具体实验方案及每次试验的样品信息如表 1所示。试验过程中首先将称量好的质量为(3.6±0.005) g的PBX造型粉分次装入模具; 然后采用材料试验机进行加载, 当预紧力为20 N时调零位移, 记录整个加载过程中的载荷-位移数据并退模; 最后将空模具材料试验机加载平台, 测量空模具20 N时位移, 进而换算PBX造型粉的初始高度L0, 试验完成后根据式(1)可得计算得PBX成型过程中的密度ρ。
| 表 1 实验方案及样品信息 Tab.1 Experimental planning and sample information |
| $ \rho = \frac{m}{{{\rm{ \mathit{ π} }}{{\left( {\frac{d}{2}} \right)}^2}({L_0} - \Delta L)}} $ | (1) |
式中, m造型粉质量,g; 为ρ为PBX成型过程中的密度, g·cm-3; L0为PBX造型粉的初始高度, mm; ΔL为压头位移, mm; d为模具内径, mm。
3 结果与讨论 3.1 实验结果处理实验所得的载荷-位移曲线, 可得两种PBX造型粉在不同压力下的压力-密度曲线, 如图 2所示。由表 1与图 2可知, PBX-B的初始高度较高, 初始密度较小, 分析认为改性添加剂诱发的粒径分布和表面力学特性改变, 及其流动性的劣化是造成PBX-B较PBX-A初始装药更松散的重要原因。压制过程中, PBX-B造型粉密度始终小于PBX-A, 同时两种PBX的密度在低压力段均增长较快, 分析认为压制初期密度的增长, 主要是通过造型粉颗粒的流动和重排填充大空隙的方式实现, 故而速率较快, 随着压力增大空隙被填满, 造型粉开始接触挤压, 密度的提升转而通过弹性变形、塑性变形和晶体破碎的方式实现, 应变硬化的现象越来越明显, 进而密度变化的速率减缓。
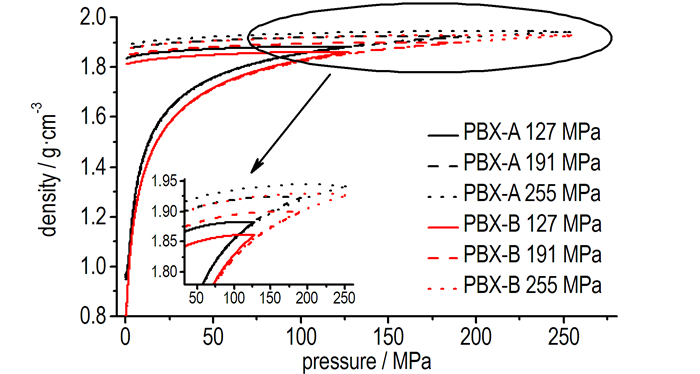
|
图 2 两种PBX造型粉在不同压力下压力-密度曲线 Fig.2 p-ρ curves of two kinds of PBX modeling powders under different pressures |
鉴于造型粉致密化压制成型过程与粉末冶金压制成型过程的相似性, 研究采用该领域广泛应用的Kawakita方程[6]和Gerdemann-Jablonski方程[11]来描述造型粉颗粒聚集体致密化过程中的加载曲线方程。其中, Kawakita方程曾被用于描述炸药晶体聚集体的压制曲线[5], Kawakita方程的具体形式如式(2)所示, 将式(3)和式(4)带入式(2)得到压力密度关系如式(5)所示。
| $ \frac{p}{C} = \frac{p}{a} + \frac{1}{{ab}} $ | (2) |
| $ a = 1 - \frac{{{\rho _0}}}{{{\rho _m}}} $ | (3) |
| $ C = \frac{{{V_0} - V}}{{{V_0}}} $ | (4) |
| $ \rho = \frac{{\left( {bp + 1} \right){\rho _0}{\rho _{\rm{m}}}}}{{{\rho _{\rm{m}}} + bp{\rho _0}}} $ | (5) |
式中, p为压力, MPa; a和b为拟合参数, a为颗粒集合体初始孔隙度; ρ0和ρm分别为颗粒初始密度和理论最大密度, g·cm-3; C为体积压缩率。
Gerdemann-Jablonski方程的数学形式如式(6)所示, 其中ρ0代表初始密度, A(1-e-arp)用于描述造型粉加载过程中的流动重排特性, B(1-e-bpp)用于描述机械硬化(包括颗粒的弹塑性变形)特性。式(6)中A和B分别表征重排和机械硬化对致密化成型密度的相对贡献, 理论最大密度ρ∞=ρ0+A+B; ar和bp反映了完成颗粒重排和机械硬化所需要的压力大小。
| $ \rho = {\rho _0} + A(1 - {{\rm{e}}^{ - {a_{\rm{r}}}p}}) + B(1 - {{\rm{e}}^{ - {b_{\rm{p}}}p}}) $ | (6) |
Kawakita方程和Gerdemann-Jablonski方程分别描述两种造型粉加载过程中压力-密度曲线的结果如图 3所示, 图 3中PBX-A和PBX-B的最大载荷均为255 MPa。二者描述精度均较高, 但相较之下Gerdemann-Jablonski方程优于Kawakita方程, 式(7)与式(8)为根据拟合结果得到的PBX-A和PBX-B的Kawakita加载曲线方程, 式(9)与式(10)分别为PBX-A和PBX-B的Gerdemann-Jablonski加载曲线方程。
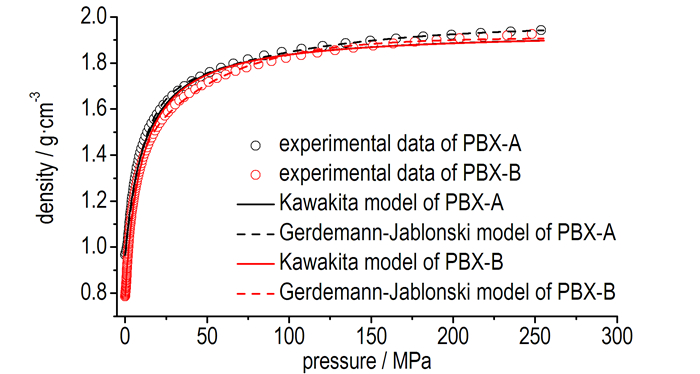
|
图 3 PBX-A和PBX-B的加载试验结果及拟合曲线 Fig.3 Loading test results and fitting curves of PBX-A and PBX-B |
| $ \rho = \frac{{0.3112p + 1.8768}}{{0.1602p + 1.942}} $ | (7) |
| $ \rho = \frac{{0.3797p + 1.5257}}{{0.1957p + 1.942}} $ | (8) |
| $ \rho = 0.966 + 0.63854\left( {1 - {{\rm{e}}^{ - p/9.87984}}} \right) + B(1 - {{\rm{e}}^{ - p/87.16516}}) $ | (9) |
| $ \rho = 0.786 + 0.56915\left( {1 - {{\rm{e}}^{ - p/5.20222}}} \right) + B(1 - {{\rm{e}}^{ - p/49.70552}}) $ | (10) |
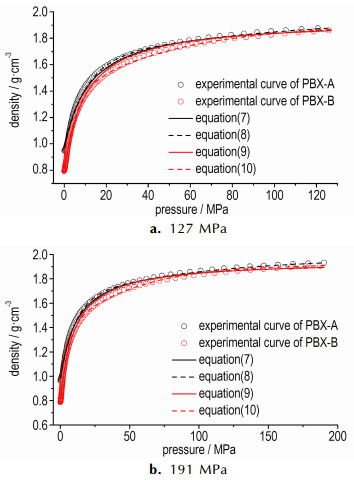
两种方程对PBX-A和PBX-B的压制曲线拟合误差如图 4所示。由图 4可知两种方程在初始压力段的误差均相对较大, 分析认为加载初期的造型粉滑移、重排与破碎是造成描述误差偏大的主要原因。同时, Gerdemann-Jablonski方程在高压力段的拟合精度明显优于Kawakita方程, 255 MPa时PBX-A的前者拟合误差为0.03%, 后者拟合误差为2.30%。在整个实验压力范围内, Gerdemann-Jablonski方程和Kawakita方程对PBX-A造型粉的压力-密度曲线拟合平均绝对误差分别为1.23%和1.79%, PBX-B造型粉的平均绝对误差分别为0.95%和1.57%。为验证前述结论的重复性, 研究中补充开展了127 MPa和191 MPa的四组实验(见表 1), 试验数据与拟合结果的对比分析结果如图 5所示, 验证了Kawakita方程和Gerdemann-Jablonski方程均可令人满意地描述两种造型粉的加载压力-密度曲线, 且Gerdemann-Jablonski方程优于Kawakita方程的结论。
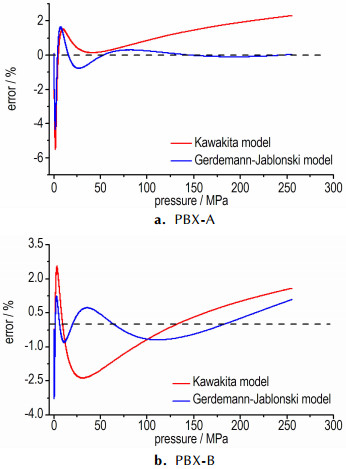
|
图 4 两种PBX拟合结果的压力-相对误差曲线 Fig.4 Pressure-relative error curves of the fitting results of two PBXs |
|
图 5 两种PBX在不同压力下的实验结果与拟合曲线 Fig.5 Experimental results and fitting curves of two PBXs under different pressures |
造型粉的加载曲线方程不仅需要具有普适的高描述精度, 其方程参数还须尽可能地与造型粉的物理性质/行为形成关联。川北公夫[6]认为Kawakita方程中的参数1/b与范德瓦耳斯方程中的气体分子间引力(范德华力)具有相近的物理意义, 并将其定义为粉末颗粒间的粘附力[10], 多种粉末颗粒的实验结果[12]研究表明: 1/b为1~100 MPa, 若将1/b看作粉末颗粒间的粘附力, 颗粒很难在如此大的粘附力作用下自由流动和分散, 因此我们认为将其看作颗粒间的粘附力是不恰当的; 谭武军等[13]认为参数的倒数1/b具有模量量纲, 能够定量评价晶体聚集体的力学性能(但并不等于实际的晶体模量), 他发现1/b的值与观察的压制曲线(密度-压力曲线)斜率大小顺序一致, 但是本研究发现1/b的量纲与压制密度-压力曲线斜率量纲不同, 因此是否可以将b与颗粒材料的物理性质联系起来还需要进一步研究[14-15]。
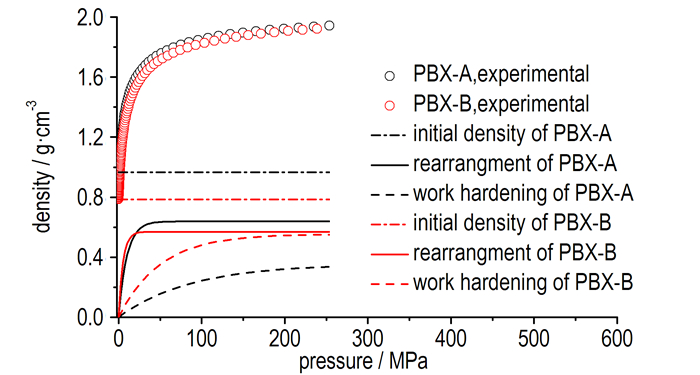
再者, PBX造型粉在致密化成型过程中存在着颗粒的滑移、重排、破碎和变形等多个阶段, 一个理想的加载曲线方程最好能够反映压制过程中的机理变化。相较之下, Gerdemann-Jablonski方程的表现更优, 图 6为颗粒初始密度、颗粒重排和颗粒机械硬化对密度的影响曲线, PBX-A和PBX-B的颗粒重排项随着压力的迅速升高, 分别在45 MPa和25 MPa达到了渐近值, 机械硬化项在200 MPa后才逐渐接近渐近值, 即在压力达到45 MPa和25 MPa之前颗粒的流动重排占据主导地位, 之后颗粒的弹塑性变形占据主导地位; 同时分析认为PBX-B造型粉改性后颗粒间摩擦力较大、粒径分布宽导致成拱较多、流动性较差及重排未充分完成就进入了机械硬化阶段, 是PBX-B造型粉颗粒重排阶段完成早于PBX-A的主要原因。
|
图 6 颗粒初始密度、颗粒重排和颗粒机械硬化对密度的影响曲线 Fig.6 The curves of effects of initial density, rearrangement and mechanical hardening of particles to density |
最后, 表 2为PBX-A和PBX-B颗粒重排和机械硬化对成型密度的相对贡献值, 两种造型粉颗粒重排对成型密度的贡献分别为64.2%和50.7%, 可见流动性差的造型粉颗粒重排较少, 而流动性好的造型粉颗粒重排较充分, 在这一阶段密度增长较多, 所以Gerdemann-Jablonski中的颗粒重排项可以反映造型粉颗粒聚集体的流动性。
| 表 2 颗粒重排和机械硬化对密度的相对贡献值 Tab.2 Relative contribution ofthe rearrangement and mechanical hardening of particles to density |
Gerdemann等[11]将ar和bp定义为完成颗粒重排和机械硬化分别所需要的压力大小, 我们认为该观点不完全合理, 这是因为:首先, ar和bp的单位为MPa-1, 与压力的量纲不同; 其次, 本研究中两种造型粉分别完成两阶段所需的压力大小和ar、bp的值并不相同, 所以ar和bp应该是与完成颗粒重排和机械硬化速率相关的两个参数; 另外也有学者认为[16]可以用ln(2/ar)和ln(2/bp)代替ar和bp来分别表示两个过程的半衰期, 此说法的科学性还需要进一步研究。
4 结论(1) Kawakita方程描述PBX-A和PBX-B造型粉加载过程中的密度演化规律时, 拟合的平均绝对误差值分别为1.79%和1.57%, 可以较高精度地描述PBX加载过程中密度演化特性; 该方程的拟合参数b虽具有模量倒数的量纲, 但遗憾目前尚无结论显示方程中的待定参数能够表达与造型粉致密化特性相关联的物理意义; 不能体现造型粉致密化成型过程中的流动重排和变形特征行为, 是Kawakita方程用于描述加载中密度演化规律的另一个不足。
(2) Gerdemann-Jablonski方程描述PBX-A和PBX-B造型粉密度演化规律的拟合平均相对误差值分别为1.23%和0.95%, 优于Kawakita方程的1.79%和1.57%;同时, Gerdemann-Jablonski方程的三项组成可分别表征造型粉颗粒的初始密度、流动重排以及机械硬化(颗粒的弹塑性变形)行为, 参数项的物理意义更为明确, 能够反映出致密化成型过程中的机理变化和不同造型粉的流动性特征, 可作为一种普适的加载曲线方程推广应用。
| [1] |
Darla Graff, Thompson, Olinger B, Deluca R. The effect of pressing parameters on the mechanical properties of plastic bonded explosives[J].
Propellants Explosives Pyrotechnics, 2005, 30(6): 391-396. DOI:10.1002/(ISSN)1521-4087 |
| [2] |
Olinger B. Compacting Plastic-Bonded Explosive molding powders to dense solids[J].
United States:Los Alamos National Laboratory(LANL), 2005: 10-38. |
| [3] |
吕珂臻, 韩超, 高铁榜, 等. 温度对RDX基PBX压制成型内部质量的影响[J].
含能材料, 2015, 23(1): 48-52. LV Ke-zhen, HAN Chao, GAO Tie-bang, et al. Influence of temperature on internal quality of pressed RDX-based PBX[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2015, 23(1): 48-52. DOI:10.11943/j.issn.1006-9941.2015.01.010 |
| [4] |
梁华琼, 雍炼, 唐常良, 等. 压制过程中PBX炸药颗粒的破碎及损伤[J].
火炸药学报, 2010, 33(1): 27-30. LIANG Hua-qiong, YONG Lian, TANG Chang-liang, et al. Crack and damage of PBX during pressing[J]. Chinese Journal of Explosives and Propellants, 2010, 33(1): 27-30. |
| [5] |
谭武军, 李明, 黄辉. RDX和HMX晶体压制方程的对比研究[J].
火炸药学报, 2007, 30(5): 8-11. TAN Wu-jun, LI Ming, HUANG Hui. Comparison study on the compaction equations for RDX and HMX granule compression[J]. Chinese Journal of Explosives and Propellants, 2007, 30(5): 8-11. |
| [6] |
Kimio Kawakita, Karl-Helmut Lüdde. Some considerations on powder compression equations[J].
Powder Technology, 1971, 4(2): 61-68. DOI:10.1016/0032-5910(71)80001-3 |
| [7] |
Heckel.R.W. Density-pressure relationships in powder compaction[J].
Trans Met Soc AIME, 1961, 221(8): 671-675. |
| [8] |
李明, 温茂萍, 黄明, 等. 压缩刚度法评价含能晶体颗粒的凝聚强度[J].
含能材料, 2007, 15(3): 244-247. LI Ming, WEN Mao-ping, HUANG Ming, et al. Evaluation of coherence strength of energetic crystalline granules by compressive stiffness method[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2007, 15(3): 244-247. |
| [9] |
Denny P J. Compaction equations: a comparison of the Heckel and Kawakita equations[J].
Powder Technology, 2002, 127(2): 162-172. DOI:10.1016/S0032-5910(02)00111-0 |
| [10] |
Huang. P.Y.
Powder metallurgy principle[M]. Beijing: Metallurgical Industry Press, 1982: 173-212.
|
| [11] |
Gerdemann S J, Jablonski P D. Compaction of titanium powders[J].
Metallurgical & Materials Transactions A, 2011, 42(5): 1325-1333. |
| [12] |
葛荣德. Kawakita粉末压制方程应用中的几个问题及方程的修正[J].
粉末冶金技术, 1993(2): 11-15. GE Rong-de. Serveral problems on application of Kawakita's powder compaction equation and its modification[J]. Powder Metallurgy Technology, 1993(2): 11-15. |
| [13] |
谭武军, 李明, 黄辉. Kawakita方程在含能晶体颗粒压制中的应用研究[J].
含能材料, 2008, 16(1): 29-33. TAN Wu-jun, LI Ming, HUANG Hui. Application of kawakita equation in compression of energetic crystalline particles[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2008, 16(1): 29-33. |
| [14] |
Adams M J, Mullier M A, Seville J P K. Agglomerate strength measurement using a uniaxial confined compression test[J].
Powder Technology, 1994, 78(1): 5-13. DOI:10.1016/0032-5910(93)02777-8 |
| [15] |
Adams M J, Mckeown R. Micromechanical analyses of the pressure-volume relationship for powders under confined uniaxial compression[J].
Powder Technology, 1996, 88(2): 155-163. DOI:10.1016/0032-5910(96)03117-8 |
| [16] |
Machaka R, Chikwanda H K. An experimental evaluation of the Gerdemann-Jablonski compaction equation[J].
Metallurgical & Materials Transactions A, 2015, 46(5): 1-7. |
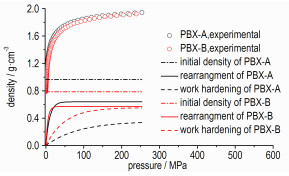
Since the description accuracy of the Gerdemann-Jablonski equation is higher than that of the Kawakita equation, and the equation parameters can reflect the flow, rearrangement, and deformation characteristics during loading process, the physical meaning is clearer and it is more worthy of popularization and application.




