2. 工业装备结构分析国家重点实验室, 辽宁 大连 116024
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian 116024, China
柱状装药和平面装药作为工业混合炸药的两种常用装药形式, 被广泛应用于火工品设计、孔内爆破和金属爆炸加工中, 研究它们的爆轰传播极限问题有着重要的实际意义。炸药在实际应用时并不存在严格意义上的理想爆轰, 这不仅是因为炸药颗粒和分布的不均匀性, 最主要的原因是对于通常所用的装药药柱, 其直径尺寸是有限的, 当爆轰波沿轴向传播时, 超高压力的反应产物发生径向膨胀, 产生向反应区内传播的径向稀疏波, 导致了反应区能量的耗散, 这种圆柱形装药爆速对直径的依赖性, 称为炸药的直径效应, 该现象的物理原理最初由苏联学者Харит он[1]提出, 而许多相关研究则是在Wood和Kirkwood[2]理论的基础上展开的。当若装药直径减小至某一临界值时, 能量耗散后反应区剩余的有效能量不足以维持稳定爆轰, 爆轰波传播随之衰减至终止, 圆柱装药的该临界值称为临界直径, 平面炸药装药则对应于临界厚度的概念。
目前测量圆柱形装药临界直径的方法一般有三种:锥形装药法、台阶法和药柱升降法[3], 第一种应用最为广泛, 其验证方法常采用验证板或光学方法记录爆轰波轨迹; 后两者虽较为直观, 但操作繁杂。而临界厚度的测量方法主要采用楔形装药, 利用验证板确定爆轰中断位置。在研究不同炸药的直径效应时, 为了获得不同装药直径下的爆速, 学者们大都采用了药柱升降法[4-6], 即用若干电探针(类型不尽相同)平行插入药柱中记录爆速的变化, 通过拟合爆速随直径的变化曲线来获取炸药的临界直径。Petel等[7]则利用台阶法和验证板测量了多种含能材料(均质液体炸药和非均质炸药)的临界直径和临界厚度, 也得到了爆速随装药尺寸变化的拟合曲线。刘玉存等[8]设计了利用一种类似台阶法的临界截面测试方法, 他们还采用楔形装药和印痕法对三种六硝基茋(HNS)装药的临界厚度进行了实验研究[9]。胡建华等[10]则利用楔形槽和铝板印痕法测量了乳化炸药爆轰的临界厚度, 上述方法在判定熄爆位置时由于验证板上的印痕一般较模糊, 测量精度并不高。
从上述研究工作可以知道, 验证板法虽然操作简便, 但在判定爆轰波中断位置时完全依靠肉眼观测, 缺乏定量的判定依据, 并且爆轰传播在过冲作用下常常在比临界值低的位置发生熄灭, 易产生误判; 而高速摄影法虽然可靠性高, 但对于野外大药量临界参数测量时设备繁杂, 现场不易操作。为了兼顾两者优点, 同时能在单次实验中就获得炸药爆速随装药尺寸的变化曲线, 本研究采用自行研制的连续压导探针, 设计了锥形和楔形两种装药形式, 对典型工业炸药——粉状ANFO炸药的爆速变化曲线进行了测量, 以此来判断炸药的熄爆位置, 获得相应的爆轰临界直径和临界厚度, 为工业炸药临界参数的测量提供一种更为方便可靠的方法。
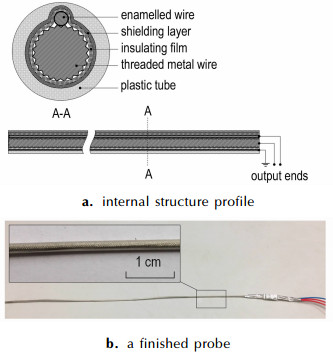
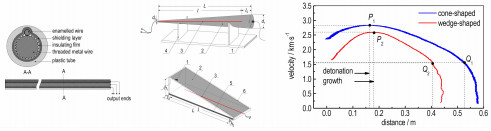
2 连续探针法测量原理与设计 2.1 连续压导探针与工作原理连续压导探针的结构如图 1a所示, 该探针由大连理工大学自行研制, 其核心元件由一端接触导通的漆包电阻丝和螺纹金属丝构成, 中间层包覆绝缘膜和屏蔽层, 最外层则由塑料套管固定, 电阻丝和螺纹丝分别作为输出端, 屏蔽层引出接地, 该新型电阻丝探针可完全依靠外界压力利用金属丝的螺纹刺破漆包层导通电阻丝, 因此不仅能用于测量爆轰波速度, 也适用于冲击波速度的测量。图 1b为实际制作完成的探针, 螺纹铁丝直径0.5~1.0 mm, 螺距0.5~0.8 mm, 漆包电阻丝直径0.04~0.1 mm, 其中漆包层厚度约0.016 mm, 成品探针直径约为2 mm, 长度根据装药情况而定, 一般为50~200 cm。
|
图 1 连续压导探针结构示意图 Fig.1 Schematic illustration of continuous pressure-conducted probe structure |
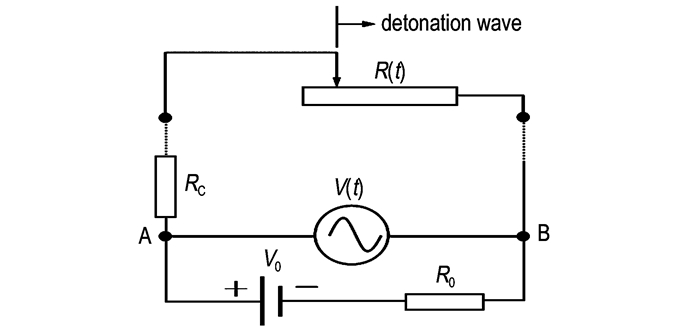
连续电阻丝探针的工作电路如图 2所示, 起爆前由于漆包层的绝缘作用, 信号采集仪显示整个电阻丝两端的电压, 炸药起爆后, 爆轰波所到之处在波阵面的高温电离和高压作用下使原本断开的金属丝与漆包电阻丝短路, 随着爆轰波的向前推进, 联入电路中的探针电阻不断减小, 信号采集仪将连续地记录探针两端的电压-时间变化, 换算后即可得到爆轰波运动的时程关系, 从而拟合得到待测炸药的爆速。
|
图 2 爆速连续测量电路图 Fig.2 Test circuit for the continuous determination of the detonation velocity |
测试电路中, Rc为回路电缆电阻, R0为内接分压电阻, 爆轰波的向前传播使探针电阻产生变化的R(t), 在恒定电压V0作用下, 由AB间示波器记录的电压变化V(t), 可得到关系式:
| $ V\left( t \right) = {\rm{ }}\frac{{R\left( t \right) + {R_{\rm{c}}}}}{{R\left( t \right) + {R_{\rm{c}}} + {R_0}}}{V_0} $ | (1) |
若已知电阻丝单位长度阻值r(标定值r=Ra/L0, Ra为探针的初始阻值, L0为探针的初始长度), 根据上式可求出被爆轰波压致导通的探针长度为:
| $ L\left( t \right) = {L_0} - {\rm{ }}\frac{{R\left( t \right)}}{r} = \frac{{{R_{\rm{a}}} + {R_{\rm{c}}} + {R_0}}}{r} - \frac{{{R_0}{V_0}}}{{r\left( {{V_0} - V\left( t \right)} \right)}} $ | (2) |
将测量得到的电压-时间曲线换算成爆轰波的时程曲线, 对此求时间的导数, 即可得到爆速为:
| $ D\left( t \right) = - {\rm{ }}\frac{{{R_0}{V_0}}}{r}{\rm{d}}\left( {\frac{1}{{{V_0} - V\left( t \right)}}} \right)/{\rm{d}}t $ | (3) |
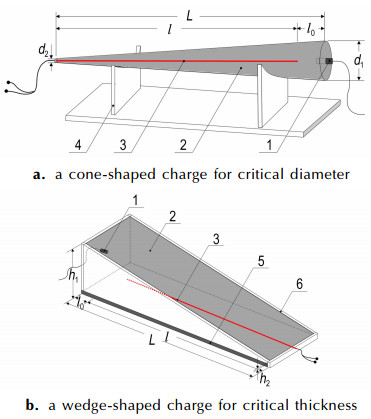
爆轰临界直径的测量采用锥形装药, 临界厚度采用楔形装药, 实验采用粉状ANFO炸药, 两者与探针的装配设计如图 3所示。锥形装药中(图 3a), 大端面直径为d1, 小端面直径d2, 圆锥总长L, 探针长l, 固定于圆锥中心, 外壳采用薄纸壳, 可近似为无约束; 楔形装药(图 3b)大端面高h1, 小端面高h2, 楔形槽长L, 探针长l, 固定于槽底, 楔形槽底采用厚度为3 mm的钢板, 四周为薄纸板框, 可近似为半约束。两种装药形式都用雷管在大端面引爆, 为了消除爆轰波形演化对测量结果的影响, 装药长度设计为足够长(大于50 cm), 并且探针头部和起爆端有一定距离(l0)。测试中传输线路采用同轴屏蔽电缆, 信号采集仪使用Pico4224示波器, 采样率为80 MSa/s。
|
图 3 炸药爆轰临界尺寸测量装置 —雷管, 2—炸药, 3—探针, 4—支架, 5—钢板, 6—纸框 Fig.3 Measuring device of the critical size for detonation of explosives 1—detonator, 2—explosive, 3—probe, 4—holder, 5—steel plate, 6—paper frame |
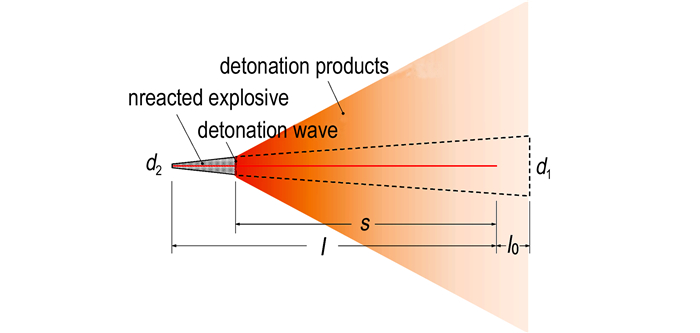
根据本研究实验装置设计的爆轰临界直径的计算模型如图 4所示, 该图表示工业炸药起爆后爆轰波停止传播时的终了状态, 此时探针在爆轰波作用下导通的最大长度为s, 根据几何关系可得到爆轰终止处的直径, 即临界直径为:
|
图 4 工业炸药爆轰临界直径计算模型 Fig.4 Calculation model of the critical diameter for commercial explosives |
| $ {d_{{\rm{cr}}}} = {d_1} - \left( {{d_1} - {d_2}} \right)\frac{{s + {l_0}}}{{l + {l_0}}} $ | (4) |
临界厚度的计算模型与图 4基本一致,其表达式也类似于式(4), 为:
| $ {h_{{\rm{cr}}}} = {h_1} - \left( {{h_1} - {h_2}} \right)\frac{{s + {l_0}}}{{l + {l_0}}} $ | (5) |
这样, 无需借助高速摄影等复杂设备, 仅利用自行研制的连续电阻丝探针便可以定量判定爆轰波终止位置, 从而计算得到炸药的临界直径和临界厚度。
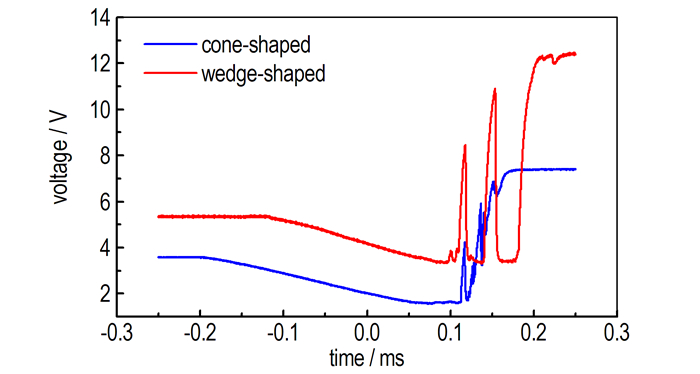
3 结果与讨论 3.1 测试数据的处理对临界直径进行了5次测试, 对临界厚度进行了2次测试, 这里以两组试验的1#试验为例, 详细说明测试数据的处理方法, 其具体装药尺寸为:对于锥形装药, d1=56 mm, d2=5 mm, l =720 mm, l0=55 mm; 对于楔形装药, h1=50 mm, h2=5 mm, l =430 mm, l0=50 mm。图 5为锥形和楔形两种装药条件下示波器记录的电压变化曲线, 从某一时刻开始(图中锥形约-0.2 ms, 楔形约-0.11 ms), 爆轰波开始作用于探针, 引起探针内电阻丝阻值的持续减小, 探针两端电压随之下降, 当装药尺寸达到某一临界值时, 爆轰波逐渐熄灭, 其高温电离和高压作用也逐渐减弱, 压导探针的“开关”效应趋于不稳定, 因此出现图 5中0.1~0.2 ms之间的信号振荡, 当爆炸完全结束时, 探针断开, 电压突跃至电源电压(图中两次实验采用了不同的电源电压)。截取振荡前的倾斜段电压信号, 应用式(2)将电压-时间曲线换算为爆轰波-冲击波时程曲线(如图 6所示)。
|
图 5 两种装药条件下的电压信号记录曲线 Fig.5 Output voltage profiles of the two shaped charge |
|
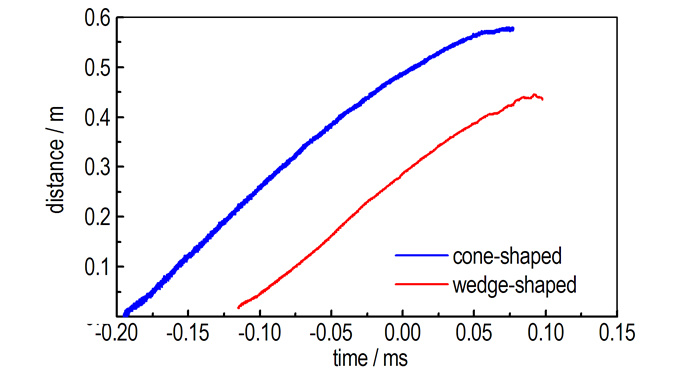
图 6 爆轰波-冲击波时程曲线 Fig.6 Time-history curves of the detonation wave-shock wave |
观察图 6可以看出, 两种装药下爆轰波的斜率随时间变化逐渐减小, 这里需要说明的是, 为了确定炸药的临界直径和临界厚度, 对于测试结果可进行两种处理方式:一是将爆轰临界参数的判定标准选为爆轰波-冲击波时程曲线斜率等于零处; 另外一种则是通过对时程曲线求导获取爆轰波和冲击波的速度变化曲线, 观察变化规律确定临界参数。采用前一种方式将会使实验值明显低于真实值, 这是因为, 一方面, 由于过度压缩的结果, 爆轰传播将会在比临界值还要低的直径处发生熄灭; 另一方面, 即使爆轰波终止后, 在炸药中还会传播冲击波, 冲击波压力也会使探针闭合导通, 因此此处探针长度的持续减小并不完全只是爆轰波的作用, 为了把这种过冲作用降低到最小, 应尽可能把锥形和楔形装药的张角做到最小[11]。由于爆轰波和冲击波在传播速度上的差异, 我们选取第二种判定方式, 对图 6曲线拟合后进一步处理, 得到如图 7所示的爆轰波-冲击波速度随探针导通距离的变化曲线。
|
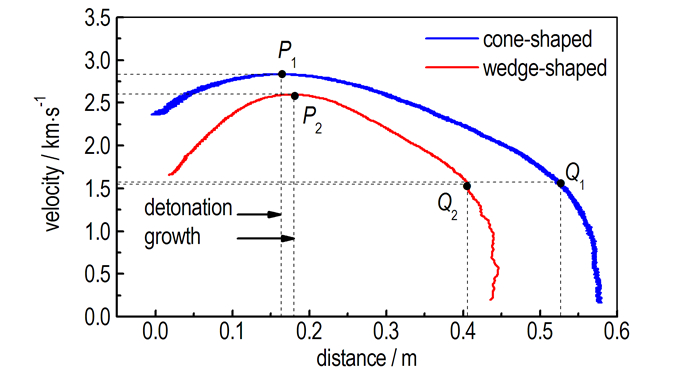
图 7 爆轰波-冲击波速度随导通距离的变化曲线 Fig.7 Dependence of the detonation wave- shock wave velocity on the conduction distance |
图 7直观地反映了两种装药条件下爆速和冲击波速度的变化过程, 尽管探针离起爆端有l0的距离(4~10 cm), 但由于粉状ANFO炸药爆轰显著的非理想性, 探针起始处依然有一端明显的爆轰成长过程, 从图 7中可以粗略判断这段距离为15~20 cm, 之后炸药爆速达到最大值Dmax(图 7中P1、P2点), 分别为2.8336 km·s-1和2.5964 km·s-1。随着装药尺寸的减小, 爆速也相应减小, 呈现出直径效应, 在约1.5 km·s-1速度时(图中Q1、Q2点), 曲线出现明显的转折, 可判定为爆轰波传播的结束, 剩余部分则为冲击波在未反应炸药内的传播, 由于没有了炸药化学反应能量的维持, 传播速度急剧衰减。这样, 由Q1、Q2的横坐标就可以得到式(4)和(5)的s值, 分别为53.03 cm和40.78 cm, 将1#试验的装药尺寸等参数代入式(4)和式(5)后, 可计算得到相应的临界直径为17.49 mm, 临界厚度为7.08 mm。
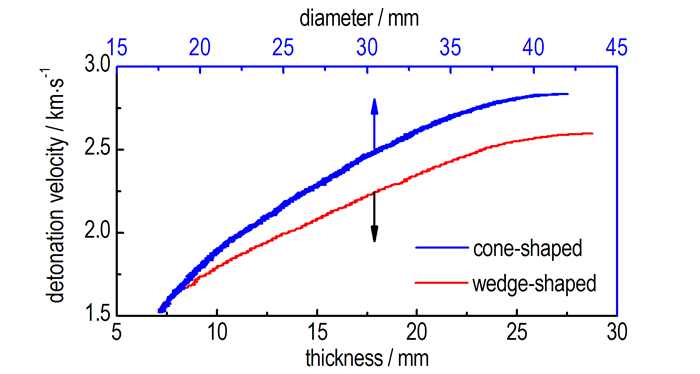
选取图 7中P1Q1和P2Q2段, 将表示距离的横坐标与式(4)和(5)中的变量s对应, 即可得到如图 8所示的爆速随装药尺寸的变化曲线, 若锥形装药和楔形装药的尺寸足够大, 则利用该曲线可以确定炸药爆轰的极限尺寸(即装药尺寸大于某一临界值时, 继续增加装药尺寸爆速不再增加)。
|
图 8 爆速随装药尺寸的变化曲线 Fig.8 Dependence of the detonation velocity on the charge size |
按照上述判定方法, 对ANFO炸药爆轰临界尺寸的测量进行了多组重复性实验, 结果汇总于表 1。
| 表 1 粉状ANFO炸药的爆轰临界尺寸 Tab.1 Detonation critical size of the powdery ANFO explosive |
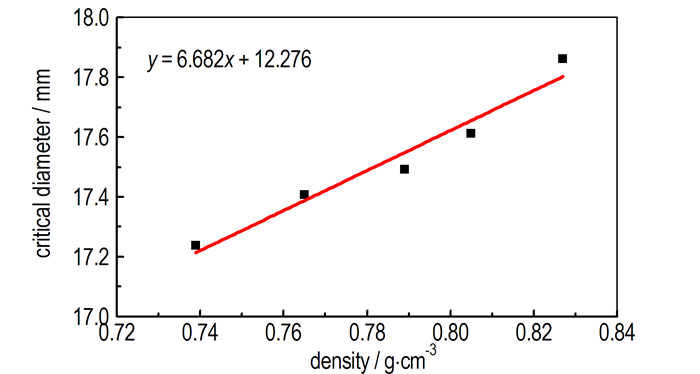
对比分析表 1中的实验结果, 并绘制图 9所示的临界直径-密度关系曲线, 可以发现如下一些规律:
|
图 9 临界直径与炸药密度的关系 Fig.9 Dependence of the critical diameter on the explosive density |
(1) 炸药密度越大, 最大爆速值Dmax也越大(临界直径中3#试验的明显异常可能是由于局部区域炸药密度和颗粒的不均匀造成的)。
(2) 由图 9可以知道, 对于粉状ANFO炸药, 在一定范围内, 随着炸药密度的增大, 其临界直径会相应地上升, 两者呈线性关系, 这与工业炸药粗颗粒、分散性、物化性质不均匀等有关。
(3) 利用前述规律, 由临界直径与密度的线性关系(图 9), 得到粉状ANFO炸药在堆放密度为0.67 g·cm-3(统一为临界厚度测试的平均密度)时的临界直径为16.75 mm(无约束), 在此密度下, 平均临界厚度为7.06 mm, 这样, 在密度为0.67 g·cm-3时, 粉状ANFO炸药的临界直径(无约束)与临界厚度(半约束)比值(dcr:hcr)为2.37, 这与相关估算值[12](3~4)和实验值[13](2.3~3)基本接近, 验证了所述方法的可靠性。
4 结论(1) 研制了一种可同时在爆轰波和冲击波压力作用下导通的连续电阻丝探针, 基于该探针分别设计了用于测定工业炸药爆轰临界直径和临界厚度的锥形和楔形装置, 给出了相应的临界参数判定公式。该法操作简单, 获取数据方便, 同时可以实现在单次实验中获得炸药爆速随装药尺寸的变化曲线, 从而定量判断爆轰波终止位置。
(2) 利用连续电阻丝探针测量了粉状ANFO炸药的临界参数, 0.67 g·cm-3密度下其平均临界直径为16.75 mm(无约束), 平均临界厚度为7.06 mm(底部钢板约束)。
(3) 对比分析实验结果发现, 粉状ANFO炸药的临界尺寸随炸药密度的增大而升高, 密度为0.67 g·cm-3的粉状ANFO炸药临界直径(无约束)与临界厚度(半约束)的比值为2.37, 与文献结论基本符合, 验证了连续电阻丝探针法可适用于工业炸药临界直径和临界厚度的测量。
| [1] |
Харит онЮ В.
Вопросы т еории ВВ[M]. -М.-Л.: Изд.АН СССР, 1947: 7-28.
|
| [2] |
Wood W W, Kirkwood J G. Diameter effect in condensed explosives. The relation between velocity and radius of curvature of the detonation wave[J].
The Journal of Chemical Physics, 1954, 22(11): 1920-1924. DOI:10.1063/1.1739940 |
| [3] |
孙承纬, 卫玉章, 周之奎.
应用爆轰物理[M]. 北京: 国防工业出版社, 2000: 216-239.
SUN Cheng-wei, WEI Yu-zhang, ZHOU Zhi-kui. Applied detonation physics[M]. Beijing: National Defense Industry Press, 2000: 216-239. |
| [4] |
Campbell A W. Diameter effect and failure diameter of a TATB-based explosive[J].
Propellants, Explosives, Pyrotechnics, 1984, 9(6): 183-187. DOI:10.1002/(ISSN)1521-4087 |
| [5] |
谭多望, 方青. 常温下钝感炸药爆轰波传播的曲率效应研究[J].
含能材料, 2005, 13(1): 13-16. TAN Duo-wang, FANG Qing. Curvature effect for insensitive explosive at normal atmospheric temperature[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2005, 13(1): 13-16. |
| [6] |
Bdzil J B, Aslam T D, Catanach R A, et al. DSD front models: nonideal explosive detonation in ANFO[R]. Los Alamos National Laboratory, 2002.
|
| [7] |
Petel O E, Mack D, Higgins A J, et al. Comparison of the detonation failure mechanism in homogeneous and heterogeneous explosives[C]//Proc. 13th Symp. Int. on Detonation. 2006: 2-11.
https://www.researchgate.net/publication/257433471_Comparison_of_the_Detonation_Failure_Mechanism_in_Homogeneous_and_Heterogeneous_Explosives |
| [8] |
陆春荣, 刘玉存. RDX的粒度对临界截面积的影响[J].
中北大学学报, 2004, 25(5): 368-370. LU Chun-rong, LIU Yu-cun. Effect of RDX particle size on critical diameter[J]. Journal-North China Institute of Technology, 2004, 25(5): 368-370. |
| [9] |
王建华, 刘玉存, 刘登程, 等. HNS的临界厚度测试研究[J].
含能材料, 2008, 16(2): 146-148. WANG Jian-hua, LIU Yun-cun, LIU Deng-cheng, et al. Critical thickness of HNS[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2008, 16(2): 146-148. |
| [10] |
胡建华, 高宏伟, 张立. 乳化炸药的临界爆轰直径的实验研究[J].
爆破, 2015, 32(3): 156-161. HU Jian-hua, GAO Hong-wei, ZHANG Li. Experimental of critical detonation diameter of emulsion explosive[J]. Blasting, 2015, 32(3): 156-161. |
| [11] |
Ferm E N, Mariam F, LANSCE Proton Radiography Team. Proton radiography observations of the failure of a detonation wave to propagate to the end of a conical explosive charge[C]//Proceeding of the 14th American Physical Society Topical Meeting: Shock Compression of Condersed Matter 2005, 2006, 845(1): 968-971.
|
| [12] |
奥尔连科. 爆炸物理学[M]. 孙承纬, 译. 北京: 科学出版社, 2011: 293-315.
Opjieko L P. Explosion Physics[M]. SUN Cheng-wei, Beijing: Science Press, 2011: 293-315. |
| [13] |
АфанасьевГ Т, БедовВ И, СергиенкоО И. Дет онационная способност ь т вердых ВВ при высокой плот ност и[J].
Физика горения и взрыва, 1981, 17(2): 158 |
A novel velocity probe was developed, which could be used for continuous measurement of detonation and shock velocity. Based on the probe, unconstrained cone-shaped charge and semi-constraint wedge-shaped charge were designed to determine the critical diameter and thickness respectively. The detonation-shock velocity curves of ANFO under the two conditions were obtained, from which the corresponding critical diameter and thickness were calculated. The relationship between the diameter, thickness and explosive density was analyzed.




