液体燃料作为化石燃料的一种, 广泛应用于石油、化工、塑料和橡胶等工业生产中[1], 伴随着液体燃料云雾爆炸事故的频繁发生, 液雾爆炸机理的研究对改善设备、事故预防具有重要的意义。液雾是由液滴群、液滴蒸发的气体、空气组成的混合物, 爆炸威力在一定条件下高于其纯气相与空气的混合物[2]。目前, 国内外针对液雾爆炸已展开广泛研究, 但研究主要集中在单个液滴的蒸发与燃烧、气相两相云雾的起爆能量和爆轰波结构等方面, 对于液雾粒径的研究则相对较少。刘雪岭[3-4]对正烷烃云雾的爆炸进行了实验研究, 发现在一定的浓度范围内, 与粒径在5~15 μm范围之外的云雾爆炸相比, 云雾粒径在5~15 μm的爆炸强度较高, 而且化学当量比条件, 气相爆炸强度依然高于气液两相云雾。Williams[5]预测云雾粒径为8 μm<d<15 μm时, 存在一种“转变区域”(transition range), 并指出在该区域, 云雾爆炸强度会出现激增现象。Polymeropoulos[6]通过理论计算方法对单分散云雾燃烧速率进行了研究并预测, 云雾粒径为5~15 μm时, 液滴燃烧速率有一个明显的增加现象。Bowen P J等[7-11]研究发现粒径在7~15 μm之间的液雾具有更高的燃烧速度, 并指出“transition range”发生在10 μm左右, 低于10 μm的液雾燃烧接近纯气相燃烧。对于5~15 μm的“转变区域”, 国外进行了大量的仿真和实验研究, 但并没有形成统一可靠的结论被沿用[7], 国内仅有少数相关实验有所涉及[3], 并没有关于此的仿真研究。基于此, 本研究利用FLUENT数值计算软件, 模拟了粒径为0~18.1 μm的庚烷液雾在20 L球形爆炸罐体内的扩散及爆炸过程, 并将数值模拟与文献结果进行对比分析, 以期得到粒径对庚烷液雾爆炸参数的影响规律。
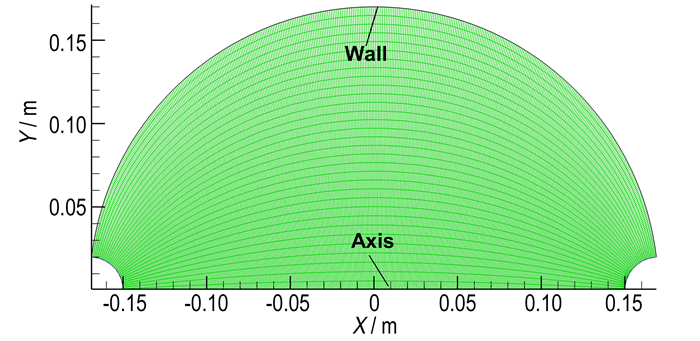
2 模型的建立 2.1 建立二维模型以图 1所示的实验装置[12]为基础, 模拟20 L球形爆炸容器内庚烷(C7H16)液雾的扩散和爆炸情况。由于20 L球形密闭爆炸容器为轴对称结构, 为了减小计算量, 将其简化为柱坐标系下的二维模型,见图 2。图 3为喷嘴的简化设计模型。

|
图 1 模拟计算的实验装置 1—20 L圆形爆炸装置, 2—压力传感器, 3—点火电极, 4—喷嘴, 5—储料盒, 6—电磁阀, 7—点火及控制系统, 8—信号采集系统, 9—储气室 Fig.1 Experimental apparatus of simulation 1—20 L spherical explosive device, 2—pressure sensors, 3—ignition electrode, 4—nozzle, 5—fuel container, 6—solenoid valve, 7—ignition and control system, 8—signal acquisition system, 9—air compression chamber |
|
图 2 球形容器简化模型 Fig.2 Simplied model of spherical vessel |

|
图 3 喷嘴简化模型 Fig.3 Simplied model of spary nozzle |
研究忽略一次雾化过程, 即以假定粒径的庚烷液滴在一定的压力下喷进罐体, 按20 L罐体内燃料与空气完全燃烧反应喷进1.6 g的C7H16, 忽略壁面损耗, 控制喷雾压力和浓度不变, 改变初始粒径以获得不同索特直径(D32)的液雾场。
庚烷(C7H16)常温下为液体, 沸点98.5 ℃[3], 研究假定庚烷与空气燃烧反应过程为单步不可逆的, 反应方程为C7H16+11O2→7CO2+8H2O。因研究中所计算的庚烷液滴粒径(微米级)较小, 且有蒸发, 所占体积可忽略不计, 液滴扩散过程中考虑液滴之间的相互碰撞、液滴与气体之间的相互作用。为了计算精确, 同时还考虑了热泳力、曳力、升力和虚拟质量力, 忽略重力。D32常在燃烧和蒸发现象中被用来代表单分散性液雾的当量直径, 本研究中一律采用D32表示液雾的粒径, 见式(1)[13]。
| $ {{D}_{32}}=\frac{{{D}_{\rm{m}}}}{1+\alpha {{e}^{-4{{\delta }^{2}}}}} $ | (1) |
式中, Dm表示液滴的最大尺寸, m; α为无因次常数, 无量纲; δ为液滴尺寸常数, 无量纲。
为了与实验条件相吻合, 模拟更真实的情况, 研究忽略了喷雾过程中带进的空气, 点火之前把爆炸罐体内的压力设置为一个标准大气压和蒸发的庚烷产生的分压的总值。
2.3 控制方程通过求解Navier-Stokes偏微分方程(2)~(5)得到庚烷液雾爆炸过程中的气相流动。
质量守恒方程为:
| $ \frac{\partial \rho }{\partial t}+\frac{\partial }{\partial {{x}_{i}}}\left( \rho {{u}_{i}} \right)={{S}_{\rm{m}}} $ | (2) |
式中,ρ为密度, kg·m-3; t为时间, s; xi是空间坐标在i方向上的分量, m; ui是速度矢量在i方向上的分量, m·s-1; Sm为源项, 为来自液滴的质量通量;
动量守恒方程为:
| $ \frac{\partial }{\partial t}\left( \rho {{u}_{i}} \right)+\frac{\partial }{\partial {{x}_{i}}}\left( \rho {{u}_{i}}{{u}_{j}} \right)=-\frac{\partial p}{\partial {{x}_{i}}}+\frac{\partial {{\tau }_{ij}}}{\partial {{x}_{i}}}+\rho {{g}_{i}}+{{F}_{i}} $ | (3) |
式中,p为静压, Pa; τij是应力张量, gi和Fi分别是i方向上的重力体积力和外部体积力, N。
| $ {{\tau }_{ij}}=\left[\mu \left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right) \right]+\lambda \mu \frac{\partial {{u}_{i}}}{\partial {{x}_{i}}}{{p}_{ij}} $ | (4) |
式中,μ为动力粘度, N·s·m-2; λ为第二粘度, 一般可取-2/3。
能量守恒方程为:
| $ \begin{align} &\frac{\partial }{\partial t}\left( \rho E \right)+\frac{\partial }{\partial {{x}_{i}}}\left[{{u}_{i}}~\left( \rho E+p \right) \right]= \\ &\frac{\partial \left( {{K}_{\rm{eff}}}\frac{\partial T}{\partial {{x}_{i}}}-\sum\limits_{j\prime }{{{h}_{j}}\prime \overset{\to }{\mathop{{{J}_{j}}\prime }}\, }+{{u}_{j}}{{\left( {{\tau }_{ij}} \right)}_{\rm{eff}}} \right)}{\partial {{x}_{i}}}+{{S}_{h}} \\ \end{align} $ | (5) |
式中,Keff是有效导热系数, 无量纲;
液滴的扩散考虑为两相流问题, 采用了离散相模型[14], 通过对拉氏坐标下颗粒作用力微分方程积分求解液滴的轨迹, 采用斯托克斯方程追踪(随机轨迹)轨迹模型, 颗粒所受作用力平衡方程在笛卡尔坐标系下的形式为:
| $ \frac{\partial }{\partial t}({{u}_{\rm{p}}})={{F}_{\rm{D}}}(u-{{u}_{\rm{p}}})+\frac{{{g}_{x}}}{{{\rho }_{\rm{p}}}}({{\rho }_{\rm{p}}}-\rho )+{{F}_{x}} $ | (6) |
式中,u为气相速度, m·s-1; up为颗粒速度, m·s-1; ρ为气体密度, kg·m-3; ρp为颗粒密度, kg·m-3;
液滴的传热/蒸发, 计算中使用一个简单的热平衡方程[14](6)来关联颗粒温度Tp(t)与颗粒表面的对流和辐射传热, 当颗粒的温度小于其蒸发温度(Tp<Tvap)时, 液滴与流体之间没有质量交换, 当液滴穿过流体单元(计算网格)时, 液滴吸收(释放)的热量作为源相作用到连续相的能量方程中:
| $ {{m}_{\rm{p}}}{{c}_{p}}\frac{{\rm{d}}{{T}_{\rm{p}}}}{{{\rm{d}}_{t}}}=h{{A}_{\rm{p}}}\left( {{T}_{\infty }}-{{T}_{\rm{p}}} \right)+{{\varepsilon }_{\rm{p}}}{{A}_{\rm{p}}}\sigma \left( \theta _{R}^{4}-T_{p}^{4} \right) $ | (7) |
式中,mp为颗粒质量, kg; cp为颗粒比热, J·(kg·K)-1; Ap为颗粒表面积, m2; T∞为连续相的当地温度, K; h为对流传热系数, W·(m-2·K-1); εp为颗粒黑度(辐射率), 无量纲; σ为斯蒂芬孙-玻尔兹曼常数, 5.67×10-8 W·(m-2·K-4); θR为辐射温度, K; 式(6)中假设颗粒内部热阻为零, 即自身温度处处一致。
当Tvap<Tp<Tbp时, Tbp为液滴的沸腾温度, 液滴温度通过自身的热平衡得出, 热平衡的计算式中把液滴的焓变与两相间的对流传热、汽化潜热联系起来:
| $ {{m}_{\rm{p}}}{{c}_{p}}\frac{{\rm{d}}T}{{\rm{d}}t}=h{{A}_{\rm{p}}}\left\{ {{T}_{\infty }}-{{T}_{\rm{P}}}+\frac{{\rm{d}}{{m}_{\rm{p}}}}{{\rm{d}}t}{{h}_{\rm{fg}}}+{{\varepsilon }_{\rm{p}}}{{A}_{\rm{p}}}\sigma \left( \theta _{R}^{4}-T_{\rm{P}}^{4} \right) \right\} $ | (8) |
式中, cp为颗粒(定压)比热, J·(kg·K)-1; Tp为液滴的温度, K;
液滴与气相流体之间传质的计算中, 液滴的蒸发量由梯度扩散[14]确定, 即从液滴向气相的扩散率与液滴与气流主流之间的蒸汽浓度梯度相关联:
| $ {{N}_{i}}={{k}_{i}}\left( {{C}_{i, s}}-{{C}_{i, \infty }} \right) $ | (9) |
式中, Ni为蒸汽的摩尔流率, kmol·(m-2·s-1); ki为传质系数, m·s-1; Ci,s为液滴表面的蒸汽浓度, kmol·m-3; Ci,∞为气相主流的蒸汽浓度, kmol·m-3; 滴表面的蒸汽分压假定等于液滴温度Tp所对应的饱和压力psat, 则此时
湍流模型采用了两方程的标准k-ε模型[14], 通过求解关于湍动能k和耗散率ε的守恒方程来得到流体的湍流流动, 其中k为湍动能, m2·s-2, ε为耗散率, m2·s-3。
气相燃烧采用了有限速率/涡耗散模型14], 该模型考虑了化学反应和湍流混合的共同作用, 同时对Arrhenius反应速率RA和湍流混合速率RE进行计算, 并取两者中的较小值作为最终计算反应速率:
| $ R={\rm{min}}\left\{ {{R}_{A}}, {{R}_{E}} \right\} $ | (10) |
对于单步不可逆反应, 由Arrhenius公式可以得出层流化学反应速率RA为:
| $ {{R}_{A}}={{Y}_{\rm{fu}}}{{Y}_{{{\rm{O}}_{\rm{2}}}}}{{\rho }^{2}}{{A}_{\rm{fu}}}{\rm{exp}}\left( \frac{-E}{RT} \right) $ | (11) |
式中, Yfu为燃料质量分数, 无量纲, YO2为氧气质量分数, 无量纲, Afu为Arrhenius公式中的指前因子, E为活化能, J·mol-1, R为普适气体常数, 8.314 J·(mol·K)-1。
涡耗散模型认为反应速率由大涡混合时间尺度k/ε控制, 只要湍流出现(k/ε>1), 反应即可进行。通过涡耗散模型计算的湍流反应速率RE取燃料、氧化剂和产物三者反应速率Rfu, E, RO2,E, Rp,E中的最小值:
| $ {{R}_{E}}={\rm{min}}\{{{R}_{{\rm{fu}}, E}}, {{R}_{{{\rm{O}}_{\rm{2}}}\mathit{E}}}, {{R}_{{\rm{p}}, E}}\} $ | (12) |
| $ {{R}_{{\rm{fu}}, E}}={{Y}_{\rm{fu}}}\rho A\frac{\varepsilon }{k} $ | (13) |
| $ {{R}_{{{\rm{O}}_{2}}, E}}={{Y}_{{{\rm{O}}_{\rm{2}}}}}\rho A\frac{\varepsilon }{vk} $ | (14) |
| $ {{R}_{{\rm{p}}, E}}={{Y}_{\rm{p}}}\rho AB\frac{\varepsilon }{\left( 1+v \right)k} $ | (15) |
式中,Yp为反应产物的质量分数, 无量纲, v为氧气的化学计量系数(当燃料质量分数为1时), 无量纲, A、B为经验常数, 取4和0.5。
考虑气体与液滴之间的辐射传热, 辐射模型采用P-1辐射模型[14]。数值计算采用SIMPLE算法[14], 公式(2)~(15)均出自文献[14]。
2.4 参数设置将1.6 g的庚烷在20 ms内喷进20 L球形容器之后, 将压力入口(pressure-inlet)改成壁面(wall), 让液雾自行静置80 ms, 以使罐体内液雾与空气混合均匀, 100 ms时刻在容器的几何中心处点火, 点火源设置为圆形高温区域。具体参数如表 1。
| 表 1 庚烷喷雾及爆炸数值模拟参数 Tab.1 Numerical simulation parameters of spary and explosion for n-Heptane droplets |
计算中控制喷雾压力不变, 通过改变初始粒径, 得到了索特平均直径D32分别为0,6.81,10.1,12.9,18.1 μm的庚烷液雾场, 液雾总浓度为80 g·m-3。为了了解液滴的分布以及液相的浓度情况, 绘制了D32=10.1 μm条件下液雾场内液滴在不同时刻(5,10,20,40,80,100 ms)的位置分布及浓度图, 见图 4。在0~20 ms的喷雾时间内, 离散相的浓度分布梯度逐渐增大, 在20~100 ms的静置期, 没有外来气流的影响, 液滴随湍流自由运动, 液滴在靠近壁面处浓度较高, 在对称轴位置较低, 而且在80~100 ms, 罐体内液滴的分布基本稳定, 在中心位置最少, 液相浓度由中心到壁面逐渐增大, 大部分液滴集中在壁面附近。

|
图 4 液雾场内液滴不同时刻的浓度分布(单位: kg·m-3)(颜色代表离散相浓度) Fig.4 Concentration profile of n-heptane in the field of droplets at different time(unit: kg·m-3) (The color represents the discrete phase concentration) |
在喷雾的过程中, 由于外来气流的影响, 微米级的液滴随湍流运动具有很大的瞬时性, 浓度分布不均。在静置期, 液滴随湍流运动到壁面附近, 受到壁面的阻碍, 湍流减弱, 液滴速度也降低, 因此出现壁面处液滴聚集的现象。
3.2 气相庚烷浓度分布为了研究液滴在流场内的浓度分布, 选取20 L球罐内0°、45°、90°方向上具有代表向的位置作为监测区域, 分布见图 5, 监测区域半径为2 cm。图 6为D32=10.1 μm的液雾场中不同区域气相庚烷的浓度随时间的变化曲线。

|
图 5 监测区域分布 Fig.5 Distribution of monitor regions |

|
图 6 不同监测区气相庚烷浓度 Fig.6 Vapor-phase concentration of n-heptane in different monitor regions vs time |
由图 6可知, 在喷雾阶段(0~20 ms), 由于湍流的作用, 气相庚烷的浓度变化比较剧烈, 且随着蒸发量的增多, 其浓度也逐渐增大。在静置阶段(20~100 ms), 气相庚烷浓度变化趋于稳定, 且在点火时刻(100 ms)时气相庚烷的浓度在液雾场内分布均匀, 为40 g·m-3左右。
3.3 爆炸参数模拟对D32分别为0,6.81,10.1,12.9,18.1 μm(0代表纯气相)的庚烷液雾场在中心点火, 计算其爆炸压力、压力上升速率、以及火焰传播速度, 见图 7和图 8。

|
图 7 不同D32下庚烷液雾爆炸压力随时间变化曲线 Fig.7 Curves of explosion pressure of n-hepane-air mixture of gas-liquid two-phase with different D32 vs time |

|
图 8 不同D32下庚烷液雾爆炸最大爆炸压力和压力上升速率曲线 Fig.8 Curves of maximum explosion pressure/explosion pressure rise rate of n-hepane-air mixture of gas-liquid two-phase with diffetent D32 vs time |
由图 7可知, 随着庚烷液雾D32(0,6.81,10.1,12.9,18.1 μm)逐渐增大, 最大爆炸压力pmax逐渐减小, 最大值为1.01 MPa, 最小值为0.9015 MPa。图 8中, 最大爆炸压力上升速率(dp/dt)max随着庚烷液雾D32的增大总体呈下降趋势, 但在10.1μm处发生反向突变, 随后又恢复下降趋势, D32=0,6.81,10.1,12.9,18.1 μm所对应的(dp/dt)max依次为0.37571, 0.27672, 0.34217, 0.22599, 0.18439 MPa·ms-1。结果表明, 在浓度80 g·m-3条件下, 庚烷液雾D32在6.81~12.9 μm爆炸强度出现明显的增加现象, 但仍小于纯气相的爆炸强度。图 9为不同粒径下最大爆炸压力和最大爆炸压力上升速率的模拟值与实验值[3]的比较, 最大压力pmax和最大压力上升速率(dp/dt)max的模拟值与实验值的最大相对误差分别为4.9%和23.6%。

|
图 9 不同D32下爆炸压力特性的模拟值与实验值对比 Fig.9 Comparison between simulation and experimental values of n-hepane-air mixture of gas-liquid two-phase with different D32 |
利用温度场随时间的变化, 计算了不同D32条件下的液雾场燃烧时容器径向(图 2中Y方向)的火焰速度, 结果如图 10。

|
图 10 不同D32下火焰速度随容器径向距离的变化 Fig.10 Flame velocity of different D32 vs radial distance of the vessel |
由图 10可知, 火焰速度随径向距离的增加先升后降, 在径向距离小于14 cm时, 气液两相庚烷液雾的火焰传播速度均小于纯气相对应的火焰速度, 而在径向距离为14~17 cm, 则反之。纯气相庚烷的火焰速度在径向距离11 cm处达到最大, 最大值为1.27 m·s-1, 由于壁面阻碍了火焰的传播, 所以在靠近壁面处火焰速度开始下降[15]。同时, 不同D32的气液两相庚烷液雾的火焰速度在径向距离15 cm附近发生不同程度突跃, 10.1 μm突跃得最剧烈, D32=6.81,10.1,12.9,18.1 μm对应的最大火焰速度分别为1.34,5.714,1.737,1.36 m·s-1。这是因为靠近壁面处液滴相对比较密集, 在火焰到达此处时液滴瞬间蒸发产生大于化学计量比的燃料空气组合, 导致火焰速度突然增加, 随后由于壁面阻碍火焰传播, 火焰速度又迅速下降。
图 11为不同D32对应的最大火焰速度, 由图 12可以看出D32的变化在10.1 μm处突跃, 为5.714 m·s-1。对于5~15 μm的液滴, 细微的气流都可能对其产生扰动[4], 所以云雾场中液滴浓度达到绝对均匀在实际中几乎不可能, 粒径在10.1 μm爆炸强度出现激增的原因由于液相浓度的局部不均匀性, 导致某处液滴在更小的空间瞬间蒸发达到最大反应速度。此计算结果与文献[5]中Williams的预测一致。

|
图 11 不同D32下的最大火焰速度 Fig.11 Maximum flame velocity for different D32 |
(1) 庚烷液雾场D32为6.81~18.1 μm时, 液雾在自行静置80 ms之后, 液相浓度由容器中心到壁面逐渐增加, 分布稳定。气相庚烷浓度分布均匀, 不同D32液雾场中的气相庚烷浓度为40.36~63.1 g·m-3。
(2) 液雾场D32为0~18.1 μm时, 随着D32的增加, 最大爆炸压力pmax逐渐减小, 最大pmax为1.01 MPa, 最小pmax为0.90146 MPa。最大爆炸压力上升速率(dp/dt)max随D32的增加总体呈下降趋势, 在D32=0处达到最大值0.37571 MPa·ms-1, 在18.1 μm处达到最小值0.18439 MPa·ms-1, 但在D32=10.1 μm处发生反向突变, 达到的反向突变值为0.34217 MPa·ms-1。虽然液雾场的(dp/dt)max在D32=10.1 μm处发生突跃, 但仍然是纯气相(D32=0)的(dp/dt)max最大。
(3) 由不同D32液雾场的火焰传播速度变化规律可知, 火焰速度沿径向先升后降, 火焰速度的最大值按随D32的不同而变化, D32=0, 6.81, 10.1, 12.9, 18.1 μm对应的最大火焰速度值分别为1.27, 1.34, 5.714, 1.737, 1.36 m·s-1, 就不同粒径液雾场所能达到的最大火焰传播速度而言, 火焰速度在D32= 10.1 μm处的发生的突跃程度最大, 与文献[4]中Williams的预测一致。
| [1] |
汪军, 马其良, 张振东.
工程燃烧学[M]. 北京: 中国电力出版社, 2008: 27.
|
| [2] |
Gant S, Bettis R, Santon R, et al. Generation of flammable mists from high flashpoint fluids: literature review[R]. HSE Research Report RR980, 2013.
|
| [3] |
刘雪岭. 瞬态多相云雾浓度、湍流及其爆炸物理特征实验研究[D]. 北京: 北京理工大学, 2016.
LIU Xue-ling. Experimental study on transient multiphase cloud concentration, turbulence and its explosive physical characteristics[D]. Beijing: Beijing institute of technology, 2016. |
| [4] |
LIU Xue-ling, ZHANG Qi, WANG Yue. Influence of vapor-liquid two-phase n-Hexane/Air mixtures on flammability limit and minimum ignition energy[J].
Industrial & Engineering Chemistry Research, 2014, 53: 12856-12865. |
| [5] |
Williams F A. Monodisperse spray deflagration[J].
Progress in Astronautics and Rocketry, 1960, 2(1): 223 |
| [6] |
Polymeropoulos C E. Flame propagation in aerosols fuel droplets, fuel vapor and air[J].
Combustion Science and Tecnology, 1984, 40(5-6): 217-232. DOI:10.1080/00102208408923807 |
| [7] |
Bowen P J, Cameron L R J. Hydrocarbon aerosol explosion hazards:A review[J].
Institution of Chemical Engineers, 1999, 77(Part B): 22-30. |
| [8] |
Zabetakis M G. Flammability characteristics of combustible gases and vapors[R]. Bureau of Mine Washington DC, 1965.
|
| [9] |
Burgoyne J H, Cohen L.The effect of drop size on flame propagation in liquid aerosols.Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences[C]//The Royal Society, 1954, 221(1162): 375-392.
|
| [10] |
Faeth G M, Olson D R. The ignition of hydrocarbon fuel droplets in air[R]. SAE Technical Paper, 1968.
|
| [11] |
Fernando. F. Fachini. Droplet combustion[C]//19th International Congress of Mechanical Engineering, Brasilia, D F, 2007: 1-7.
|
| [12] |
沈世磊. 流动状态下含铝气固两相爆炸的力学特征[D]. 北京: 北京理工大学, 2016.
SHEN Shi-lei. Mechanical characteristics of aluminum-gas-solid two-phase explosion under flow state[D]. Beijing: Beijing Institute of Technology, 2016. |
| [13] |
Kenneth K. Kuo. 燃烧学原理[M]. 郑楚光, 袁建伟, 米建春. 武汉: 华中理工大学出版社, 1991: 321.
|
| [14] |
Fluent Incorporated.
Fluent 6.3 user's guide[M]. Cavendish: Fluent Incorporated, 2006 |
| [15] |
Qi Zhang, Wei Li, Da-Chao Lin, et al. Experimental study of gas deflagration temperature distribution and its measurement[J].
Experimental Thermal and Fluid Science, 2011, 35: 503-508. DOI:10.1016/j.expthermflusci.2010.12.001 |

The effect of the droplets size of n-heptane (C7H16) on the explosion parameters was numerically simulated with the vapor-liquid concentration of 80 g·m-3.




