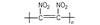热导率是表征聚合物传热能力的重要参数, 也是评估含能材料非冲击起爆、非理想爆轰的重要指标。含能聚合物可以用作为高聚物粘结炸药(PBX)的粘结剂, 其热导率的提高有利于PBX整体传热性能的改善, 提高炸药的安全性能。一些工作者利用理论计算[1-3]和实验测试[4]的方法研究了聚合物的热导率; 1983年, Datt和Masherkar[5]总结和记录了各种物质热导率的测试手段和实验数据; Caruthers[6]等整理了计算高分子聚合物热导率的经验和半经验公式; Bicerano[7]提出了仅需要用到热容、摩尔体积、摩尔Rao函数和泊松比等参数就可以估算非晶型聚合物的热导率的模型; Roy和Thoclos[8]总结了一套关于简单分子结构的气相物质的热导率的估算方法, 被广泛认为是现在基团贡献法计算热导率的最初模型, 但是它的局限性是只适合小部分化学结构; Askadskii等[9]考虑了高分子聚合物的密度和热容等参数, 链节中的原子分别在主链和支链上对热导率贡献大小以及极性基团的偶极—偶极相互作用、范德华体积等影响因素, 推导了一个精确度较高的经验公式。
本研究基于Bicerano热导率计算方法和Askadskiii热导率基团贡献法, 计算含能聚合物的热导率, 并与文献中的实验数据进行比对, 并计算了相对偏差, 通过分析共轭高聚物的导热机理, 引入含能基团, 设计了新的含能共轭高聚物, 并对其导热性能进行了预测。
2 含能聚合物热导率的计算方法 2.1 Bicerano热导率计算模型[7]Bicerano热导率计算模型仅需要用到热容, 摩尔体积, 摩尔Rao函数和泊松比等参数就可以估算聚合物在298K下的热导率。目前, 预测聚合物热导率的理论的大部分公式[10]都是基于Debye1914年提出的对于热导率的计算方法。公式如下:
| $\begin{eqnarray} λ=Λc_{v}ρuL \end{eqnarray}$ | (1) |
式中, cv是定容热容, J·kg-1·K-1; u是弹性波速度(声速), m·s-1; L是平均自由程, m; Λ是键结合常数。热传导系数h和声速u之间存在如下关系:
| $\begin{eqnarray} h=\frac{λ}{ρc_{p}}=Lu \end{eqnarray}$ | (2) |
| $\begin{eqnarray} u=(\frac{U_{R}}{V})^{3}[\frac{3(1-μ)}{1+μ}]^{\frac{1}{2}} \end{eqnarray}$ | (3) |
式(2)、(3)经过变形, 得到热导率λ的计算公式:
| $\begin{eqnarray} λ(298 \rm{K})=ρc_{p}L(\frac{U_{R}}{V})^{3}[\frac{3(1-μ)}{1+μ}]^{\frac{1}{2}} \end{eqnarray}$ | (4) |
式中,ρ是密度, kg·m-3; V是摩尔体积, m3·mol-1; UR是摩尔Rao函数, (cm3·mol-1)(cm·s-1)1/3; μ是泊松比。
2.2 Askadskii热导率计算模型[9]热量在物质中的热传导主要靠自由电子的运动(λe)和声子的振动(λL), 对于聚合物来说热传导是靠声子绕固定位置热振动, 把热能依次传递给相邻原子, 存在声子导热远大于电子导热, 即λL≫λe[11]。根据聚合物的传热机理, 有如下的热导率动态方程:
| $\begin{eqnarray} λ=c_{v}ρuL \end{eqnarray}$ | (5) |
式中, λ是热导率, W·m-1·K-1; cv是热容, J·K-1; ρ是密度, kg·m-3; u是声子传播速度, m·s-1。对于液相非晶型聚合物的热导率, 可以用描述有机液体的的热导率计算公式进行计算:
| $\begin{eqnarray} λ=A\frac{c_{p}ρ^{4/3}}{(M/m)^{1/3}} \end{eqnarray}$ | (6) |
式中, cp是定压摩尔热容, J·kg-1·K-1; ρ是密度, g·cm-3; M是链节的相对分子质量, g·mol-1; m是链节中的原子个数, A是常数, 主要取决于聚合物的化学结构, A可以表达为:
| $\begin{eqnarray} A=\frac{∑a+∑b}{N_{A}∑V_{i}} \end{eqnarray}$ | (7) |
式中, a是每一个原子的原子常数, b是极性基团的偶极·偶极相互作用, NA是阿伏伽德罗常数, Vi是每个原子的范德华体积, A3。文献[12]是关于热导率测试的实验值手册, 记录了各种聚合物热导率的实验值, 通过等式(5)和等式(6), 可以计算出参数A的取值, 再根据不同聚合物的化学结构, 可以推导出a和b的值, 见表 1。
| 表 1 原子常数和分子间相互作用力参数 Tab.1 Atomic constants and parameters describing intermolecular interactions |
根据聚合物的化学结构、密度、定压摩尔热容等参数, 通过考虑链节的相对分子质量、原子数目、不同原子分别在主链和支链上对热导率贡献大小以及极性基团的偶极—偶极相互作用、范德华体积等影响因素, 就可以采用Askadskiii的热导率计算模型计算聚合物的热导率。
2.3 聚合物热导率计算结果与实验测试值结果比较利用Bicerano和Askadskii的热导率计算模型, 得到下列聚合物热导率的计算结果, 如表 2所示。
| 表 2 不同聚合物热导率的计算值和实测值 Tab.2 Calculated values and experimental ones of thermal conductivity for different polymers |
由表 2可以看出, 大部分聚合物的热导率的实测值为0.100~0.300 W·m-1·K-1(除了PE为0.420 W·m-1·K-1), 其中含能聚合物GAP(聚叠氮缩水甘油醚)、PGN(聚叠氮缩水甘油醚硝酸酯)等的热导率比较低, 计算值小于0.250 W·m-1·K-1; 由热导率的相对偏差可知, Askadskii的热导率计算模型比Bicerano的热导率计算模型的相对偏差值更小, 和实验值相比更加接近实测值, 具有更高的可靠性和计算精度; 因此, 采用Askadskii的热导率计算模型对新设计的含能共轭聚合物进行热导率计算。
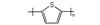
3 含能共轭聚合物的热导率计算 3.1 共轭聚合物结构性质分析共轭聚合物常被称为导电聚合物[13], 一般常见的共轭聚合物主要有聚乙炔(PA)、聚噻吩(PT)、聚吡咯(PPY)等。它们的主链是由不饱和π键组成的, 在共轭体系中, 聚合物是由双键和单键交替生长的, 共轭π体系中的π电子的流动产生了导电的可能性, 由于聚合物中的碳原子外层电子没有键合, 可以用很低的能量将电子激发, 即自由运动的电子密度比较大。没有经过掺杂处理的导电聚合物电导率很低, 属于绝缘体。其原因在于导电聚合物的能隙很宽(一维半导体的不稳定性), 室温下反键轨道(空带)基本没有电子。但经过氧化掺杂(使主链失去电子)或还原掺杂(使主链得到电子), 在原来的能隙中产生新的极化子、双极化子或孤子能级, 其电导率能达到半导体或导体的电导率范围。聚合物材料的导热主要靠晶格的振动将能量传给相邻的原子或者分子, 也就是声子导热, 因此, 由饱和α键组成主链的聚合物的导热能力比较差。而在共轭体系中[14], 若声子导热和电子导热是可以同时存在的, 则会大大提高材料的导热能力, 共轭聚合物的热导率将会比由饱和α键键组成的聚合物的热导率高得多。
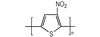
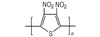
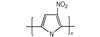
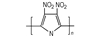
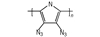
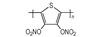
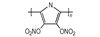
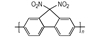
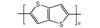
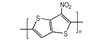
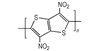
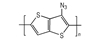
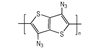
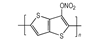
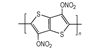
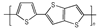
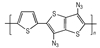
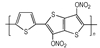
3.2 含能共轭聚合物的设计和热导率计算结果由导电聚合物为基体引入含能基团—NO2、—N3和—ONO2的方法设计了含能共轭聚合物, 并用Askadskiii的热导率计算模型对其热导率进行了评估计算结果如表 3所示。
| 表 3 含能共轭聚合物的计算参数和热导率计算值 Tab.3 Calculated parameters of energetic conjugated polymers and experimental values of thermal conductivity |
以共轭聚合物聚为基体, 在它的骨架上引入含能基团—NO2、—N3和—ONO2, 把含能聚合物的结构设计成双键和单键交替产生的共轭体系。经过Askadskiii的热导率模型计算发现, 新设计的含能共轭聚合物的热导率普遍高于由单键连接组成的通用聚合物, 热导率有了比较明显的提高, 其中后3个含能共轭聚合物的热导率可以达到1.0 W·m-1·K-1以上。而且, 当聚合物中每个链节所占体积更大时, 聚合物具有更高的热导率。
由表 2热导率的计算值和实测值可以看出, 主链为单键的通用型高分子聚合物的热导率比较低; 主链饱和的高分子聚合物是热的不良导体, 因为在通用高分子聚合物如聚乙烯中, 碳原子所有的外层电子均已键合, 不能自由移动, 能够自由运动的电子密度很低, 对于由单键组成的高分子聚合物来说热传导是主要依靠声子绕固定位置热振动, 通过声子振动把热能依次传递给相邻原子, 而且电子传热基本可以忽略不计, 即λL≫λe。
由表 3可知, 在共轭骨架上引入含能基团—NO2、—N3和—ONO2设计的新的含能共轭聚合物, 热导率提高明显。通过比较未引入含能基团和引入含能基团的共轭聚合物的热导率发现, 含能基团—NO2、—N3和—ONO2的引入对于整个聚合物的传热能力有所加强, 原因可能是这些含能基团的存在增大了聚合物链节的体积, 晶格振动导热作用加强了。共轭聚合物比非共轭聚合物的热导率明显高的原因可能是因为共轭聚合物是由双键和单键交替产生的共轭体系, 可用更低的能量将电子激发, 激发所需能量为HOMO(最高占有轨道)到LUMO(最低空轨道)间的能级差。在共轭体系中, 可能会产生晶格振动即声子导热和电子导热的耦合, 使得整个含能共轭聚合物的传导热能力增强。
4 结论(1) Askadskii和Bicerano的热导率计算模型与实验真实测试值相比, Askadskii的热导率计算模型相对偏差更小, 具有更高的可靠性。
(2) 聚合物的热导率通常比较低, 主要靠声子振动导热, 电子导热可以忽略不计, 热导率一般为0.10~0.50 W·m-1·K-1。
(3) 新设计的含能共轭聚合物的热导率要高于由单键组成的聚合物的热导率, 可能是共轭体系中存在声子振动和电子导热的耦合作用导致聚合物传导热的能力增强。
| [1] |
Krevelen D W V, Nijenhuis K T.
Properties of polymers[M]. Science Press, 2013: 1707-1719.
|
| [2] |
Luba M, Pelt T, Griskey R G, et al. Correlating and predicting polymer thermal conductivities[J].
Journal of Applied Polymer Science, 2010, 23(1): 55-58. |
| [3] |
Dashora P, Gupta G. On the temperature dependence of the thermal conductivity of linear amorphous polymers[J].
Polymer, 1996, 37(2): 231-234. DOI:10.1016/0032-3861(96)81092-5 |
| [4] |
Eiermann K, Hellwege K X. Thermal conductivity of high polymers from -180 ℃ to 90 ℃[J].
Journal of Polymer Science, 1962, 57(165): 99-106. DOI:10.1002/pol.1962.1205716508 |
| [5] |
A Datta, R A Mashelkar.
Transport pheomena in polymeric systems[M]. Wiley Eastern New Delhi, 1989.
|
| [6] |
Caruthers J M.
Handbook of diffusion and thermal properties of polymers and polymer solutions[M]. American Institute of Chemical Engineers, 1998.
|
| [7] |
Bicerno J. Prediction of polymer properties[J].
Russian Journal of General Chemistry, 2002, 81(1): 268-276. |
| [8] |
Roy D, Thodos G. Thermal conductivity of gases organic compounds at atmospheric pressure[J].
Industrial & Engineering Chemistry Fundamentals, 1970, 9(1): 71-79. |
| [9] |
Askadskii A A, Petunova M D, Markov V A. Calculation scheme for the evaluation of polymer thermal conductivity[J].
Polymer Science, 2013, 55(12): 772-777. |
| [10] |
Tempel L V D. Thermal conductivity of a glass: Ⅱ the empirical model[J].
Glass Physics & Chemistry, 2002, 28(3): 147-152. |
| [11] |
Avsec J. The combined analysis of phonon and electron heat transfer mechanism on thermal conductivity for nanofluids[J].
International Journal of Heat & Mass Transfer, 2008, 51(19): 4589-4598. |
| [12] |
Mark J E.
Physical properties of polymers handbook[M]. New York: Springer, 2007.
|
| [13] |
Gorman C B, Grubbs R H.
Conjugated polymers: the interplay between synthesis, structure and properties[M]. Conjugated Polymers. Springer Netherlands, 1991: 1-48.
|
| [14] |
Ushirokita H, Tada H. In-plane thermal conductivity measurement of conjugated polymer films by membrane-based ac calorimetry[J].
Chemistry Letters, 2016, 45(7): 735-737. DOI:10.1246/cl.160175 |