浇注型高聚物粘结炸药(PBX)以其优异的抗过载力学特性而在侵彻战斗部中得到广泛应用, 在高速碰撞过程中, PBX中的粘结剂会吸收部分能量[1-2], 并阻碍了炸药晶粒间的直接摩擦[3], 一定程度上降低了炸药的感度。由于粘结剂的弹性模量较小, 加载过程中先发生变形, 因此炸药的整体力学性能主要依赖于粘结剂的力学性能[4-5], 主要表现为粘弹性、低模量、形变能力强[6-7], 具有较大的温度相关性和应变率相关性[8-9]。弹体侵彻靶板过程中, 装药经历复杂的力学过程, 包括:装药将承受靶体通过壳体传入的冲击波作用、高惯性载荷作用以及冲击波反射后的来回跌宕作用[10-11]。在这种低强度长脉冲[12]的非冲击加载条件下, 炸药可能出现局部损伤甚至产生热点[13], 进而发生非冲击点火, 影响侵彻安全性。为了描述PBX的力学性能和非冲击点火情况, Bennett等人[14]基于SCRAM裂纹统计模型[15], 把炸药的应力应变响应分为裂纹体的响应和粘弹性体的响应, 粘弹性体的响应则采用5个并联的Maxwell体来表征, 并认为炸药裂纹的界面摩擦是非冲击点火的主要因素。E.M. Mas等[16]在不同应变率、不同温度下测量PBX9501的应力应变曲线, 同时测量了与应变率和温度相关的动态储能模量, 并由此建立了一种线粘弹性的Maxwell模型。以上研究均使用粘弹性模型描述PBX炸药的力学响应, 但考虑的损伤模式均较为单一。而陈鹏万[17]等人的实验研究表明PBX在不同受力环境下产生的主要损伤各不相同。压缩状态下孔隙明显减少, 在拉伸状态下较容易发生粘结剂界面脱粘现象, 随着应变率和压力的增大晶体开始破碎。
基于此, 本研究考虑了炸药晶粒间的孔隙压塌, 炸药晶体的断裂破碎以及炸药晶粒与粘结剂间的脱粘三种损伤, 使用粘弹性本构模型描述浇注型PBX炸药, 通过准静态单轴压缩实验、动态霍普金森杆实验校核参数, 并利用数值模拟方法, 分析了含装药弹体侵彻混凝土薄板过程中应力波的传播, 装药压力分布和三种损伤的演化, 为深入理解炸药装药结构经历的应力应变特征提供了参考, 通过对药柱内损伤分析预测了可能发生点火的危险位置。
2 炸药的含损伤粘弹性本构模型 2.1 含损伤粘弹性本构模型炸药本构的粘弹性部分由22个maxwell体与一个弹簧并联而成。其应力增量表达式写为体积应力和偏应力两部分。
| $\begin{eqnarray} Δσ_{ii}=\frac{1}{3}Δσ_{kk}+Δσ′_{ii}~~~(i=1,3) \end{eqnarray}$ | (1) |
| $\begin{eqnarray} Δσ_{ij}=Δσ′_{ij}~~(i≠j,i,j=1,3) \end{eqnarray}$ | (2) |
式中, Δσ是应力增量, Pa。通常认为体积模量是与时间无关的量[18], 因此体积瞬态模量为零, 体积应力增量表达式为
| $\begin{eqnarray} Δσ_{kk}(ξ_{n})=\left[1-α(\bar{ε}_{eq},T)\right]\left[3K_{∞}d_{t}Δε_{kk}(ξ_{n})\right] \end{eqnarray}$ | (3) |
式中,α(
根据时域的prony级数[16], 偏应力增量表达式为
| $\begin{eqnarray} &&Δσ′_{ij}(ξ_{n})=\\ &&\left[1-α(\bar{ε}_{eq},T)\right]\left[2G_{∞}Δε′_{ij}(ξ_{n})+∑\limits^{M}_{m=1}2d^{s}_{r}\frac{G_{m}ρ_{m}}{Δξ}(1-\text{e}^{-Δξ/ρ_{m}})Δε′_{ij}(ξ_{n})+Δσ′^{R}_{ij}\right]\\ &&-Δα(\bar{ε}_{eq},T)σ′_{ij}(ξ_{n-1}) (i,j=1,3) \end{eqnarray}$ | (4) |
式中, Gm是瞬态剪切模量, Pa, Δε′ij(ξn)是应变偏量的增量, ξ是有效作用时间, ρm是相对作用时间。其中,
| $\begin{eqnarray} Δσ′^{R}_{ij}=∑\limits^{N}_{m=1}-(1-\text{e}^{-Δξ/ρ_{m}})ω_{ij}(ξ_{n})~~(i,j=1,3) \end{eqnarray}$ | (5) |
| $\begin{eqnarray} ω_{ij}(ξ_{n})=2G_{m}d_{t}d_{r}\dot{ε}_{ij}ρ_{m}(1-\text{e}^{-Δξ/ρ_{m}})+ω_{ij}(ξ_{n-1})\text{e}^{-Δξ/ρ_{m}} \end{eqnarray}$ | (6) |
式中, dr为晶体内的断裂破碎系数, 该损伤与应变率相关, 当应变率大于
| $\begin{eqnarray} d^{s}_{r}=\left\{ \begin{array}{l} 1.0-\text{exp}\left[-\dot{\bar{ε}}^{eq}/\dot{ε}_{c}\right]&if~\dot{ε}≥\dot{ε}_{c}(T)\\ 1&if~\dot{ε}<\dot{ε}_{c}(T) \end{array} \right. \end{eqnarray}$ | (7) |
式中,
表示孔隙压塌的的损伤系数dt, 采用以下指数形式[19]:
| $\begin{eqnarray} d_{t}=β+\left[1-β\right]\frac{1-\text{e}^{-\bar{ε}^{kk}_{\text{max}}/ε_{0}}}{\bar{ε}^{kk}_{\text{max}}/ε_{0}},0≤β≤1 \end{eqnarray}$ | (8) |
式中,
在拉伸作用下, 整个复合炸药的力学性能主要表现为粘结剂的力学性能, 炸药晶粒与粘结剂间的界面脱粘损伤更容易发生, 界面脱粘损伤是准静态拉伸和拉伸蠕变下的主要损伤机制。对于这样的失效用损伤系数α(
| $\begin{eqnarray} &&\dot{α}(\bar{ε}_{eq},T)=C(T)\left[1-α\right]^{m}\bar{ε}^{n}_{eq}~\text{for}~\dot{\bar{ε}}_{eq}>0~\text{and}~α≤1\\ &&\dot{α}=0~\text{for}~\dot{\bar{ε}}_{eq}≤0~\text{or}~α=1 \end{eqnarray}$ | (9) |
式中, C(T)为温度相关的常数,
| $\begin{eqnarray} \bar{ε}_{eq}=\sqrt{\frac{3}{2}ε′_{ij}ε′_{ij}} ,\dot{\bar{ε}}_{eq}=\sqrt{\frac{3}{2}\dot{ε}′_{ij}\dot{ε}′_{ij}} \end{eqnarray}$ |
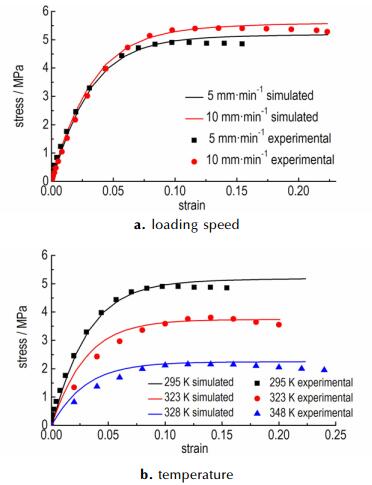
针对PBX的准静态性能和动态性能, 分别进行了准静态单轴拉压实验和动态霍普金森杆实验, 并通过数值模拟, 得到了不同加载速率和不同温度下的准静态单轴压缩应力应变关系, 与实验数据进行了对比, 图 1a为室温时不同加载速率下的准静态单轴压缩实验结果和计算结果对比, 由图 1a可知, 当加载速率由5 mm·min-1上升为10 mm·min-1, 其最大应力由4.5 MPa上升为5.3 MPa; 图 1b是加载速率为5 mm·min-1时, 不同温度下的实验和计算结果对比, 由图 1b可知, 温度从室温升高至75 ℃时最大应力下降到2.1 MPa。使用该本构模型得到的计算结果与实验结果较为一致, 能较好地体现出材料的应变率硬化效应和温度软化效应。
|
图 1 不同压缩速率和温度应力应变关系实验和计算结果对比 Fig.1 Comparison of experimental and calculated results for stress-strain relationship at different compression rate and temperature |
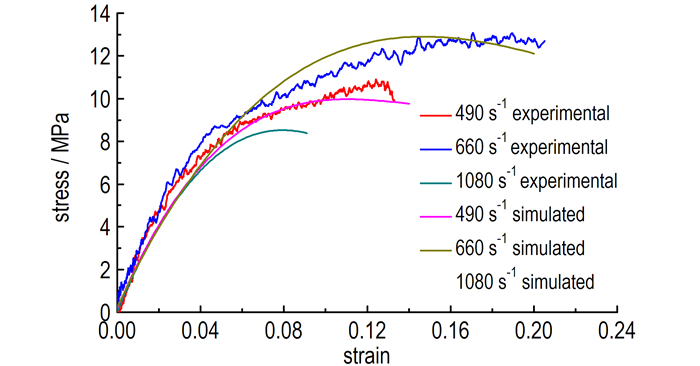
数值模拟得到了霍普金森杆撞击下的动态应力应变关系, 并与490, 660, 1080 s-1的三种应变率下得到的实验数据进行了对比, 如图 2所示, 由图 2可知, 随着加载应变率的增大, 最大应力从8.7 MPa上升到了13.1 MPa, 计算结果与实验结果一致性较高。
|
图 2 不同应变率下应力应变关系对比 Fig.2 Comparison of stress-strain relationships at different strain rates |
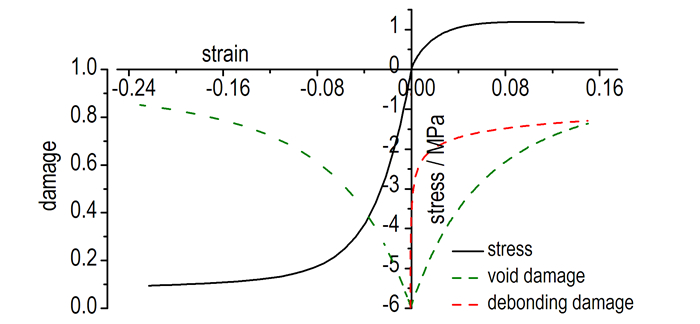
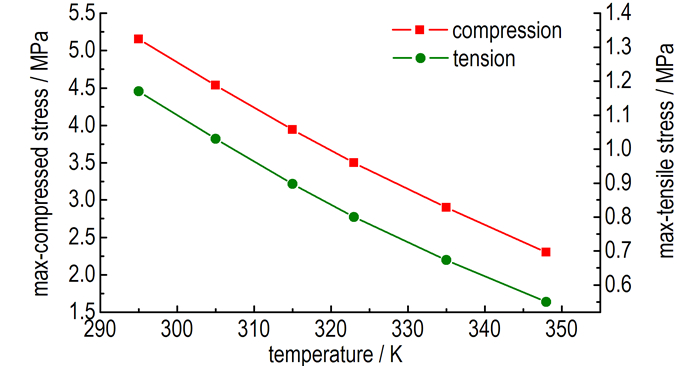
22 ℃, 10 mm·min-1的加载速率下, 采用粘弹性模型对直径为Φ20 mm×20 mm的圆柱进行单轴拉压模拟, 应力应变关系和损伤演化如图 3所示。由图 3可知, 最大压缩应力为5.3 MPa, 最大拉伸应力为1.17 MPa, 大约为最大压缩应力的1/5, 拉伸过程中粘结剂的力学性能占据主导, 炸药晶粒和粘结剂间容易发生界面脱粘现象导致拉伸失效, 孔隙压塌损伤贯穿整个受力过程, 在准静态加载过程中, 炸药晶体的断裂破碎不容易发生。不同温度下最大拉伸应力、最大压缩应力与温度的关系如图 4所示, 由图 4可知, 随着温度的上升, 最大拉伸应力、最大压缩应力都呈线性下降。
|
图 3 准静态加载下的应力应变关系 Fig.3 Stress-strain relationship under quasi-static loading |
|
图 4 最大拉伸和压缩应力与温度的关系 Fig.4 The relationship between maximum tensile and compressive stress and temperature |
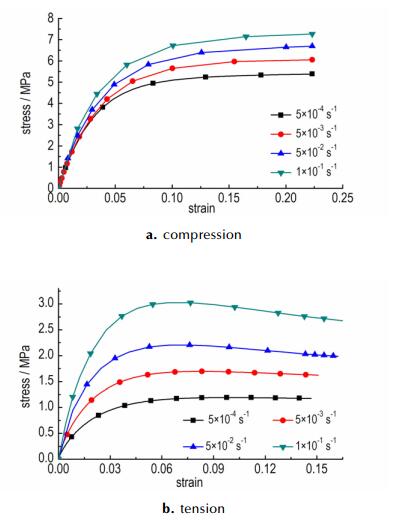
PBX材料不仅具有明显的温度软化效应, 还存在一定程度的应变率硬化效应[10-13]。图 5为不同应变率下(5×10-4 ~1×10-4 s-1)的单轴压缩和拉伸的应力应变关系对比, 由图 5可知, 压缩产生的最大应力从5.3 MPa上升到了7.2 MPa, 提高了35%, 而拉伸的最大应力从1.17 MPa提高到3.02 MPa, 提高了1.5倍, 这是由于拉伸过程中, 材料的整体性能更依赖于粘结剂的力学性能, 因此应变率硬化效应也更为敏感。
|
图 5 不同应变率下压缩拉伸应力应变关系实验和计算结果对比 Fig.5 Comparison of experimental and calculated results for the stress-strain relationship of compression and tension at different strain rates |
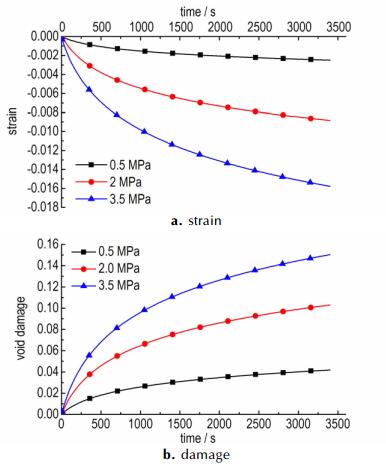
压缩蠕变和拉伸蠕变的加载压力分别为单轴压缩和单轴拉伸的最大应力的10%, 40%和70%, 加载速度为5 mm·min-1, 后保持该应力不变使材料蠕变两个h。图 6a为压缩蠕变在不同压力下应变与时间的关系(在处理数据时已经将总应变减去初始应力达到预设值时的应变值), 压缩蠕变过程中只产生孔隙压塌损伤, 该损伤随时间的演化如图 6b所示。
|
图 6 不同压力下的压缩蠕变和损伤演化 Fig.6 Compression creep and damage evalution at different pressures |
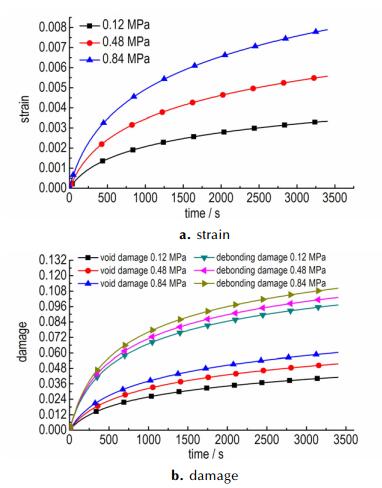
在不同拉伸强度下应变与时间的关系如图 7a所示, 对应拉伸蠕变产生的损伤随时间演化如图 7b所示。在拉伸状态下炸药材料产生孔隙压塌损伤较小, 而粘结剂脱粘损伤较大, 脱粘损伤的增长导致了拉伸蠕变比压缩蠕变相对更快。
|
图 7 不同压力下的压缩蠕变和损伤演化 Fig.7 Compression creep and damage evalution at different pressures |
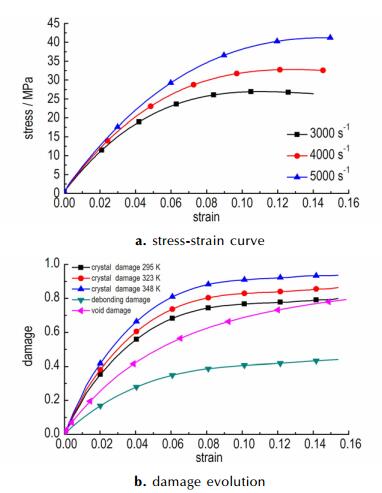
已有研究[17]表明, 当PBX受到冲击载荷作用时, 较容易发生晶体破碎损伤, 在扫描电镜下可观察到炸药晶体的裂纹甚至断裂现象。通过计算模拟了不同应变率和不同温度下霍普金森杆实验得到的应力应变关系和不同应变率下损伤随应变的演化, 见图 8。由图 8可知, 随着应变率的增大, 晶体破碎损伤增大, 而粘结剂脱粘损伤和孔隙压塌损伤与应变率并无直接关系。
|
图 8 不同应变率下的应力应变曲线和损伤演化 Fig.8 Stress-strain curves and damage evolution at different strain rates |
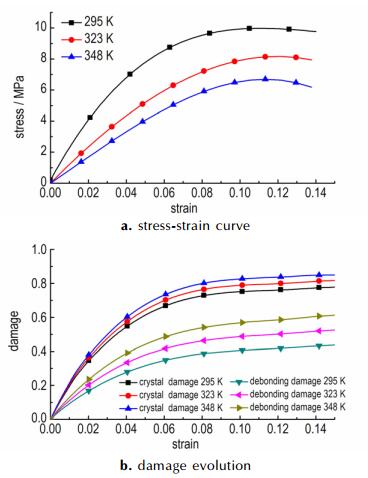
图 9为模拟的不同温度下霍普金斯杆撞击得到的应力应变关系和损伤随应变演变历史。由图 9可知, 较高应变率下PBX的本构关系依然存在高度的温度相关性, 其最大应力随温度的升高而降低。同时, 随着温度的升高, 晶体破碎损伤的最大值从0.78上升到0.85, 而粘结剂脱粘损伤的从0.44上升到了0.66, 说明温度对粘结剂脱粘损伤的影响更大, 符合实际加载过程中温度对粘结剂力学性能的影响大于炸药晶粒力学性能影响这一特征。
|
图 9 不同温度下的应力应变曲线和损伤演化 Fig.9 Stress-strain curves and damage evolution at different temperature |
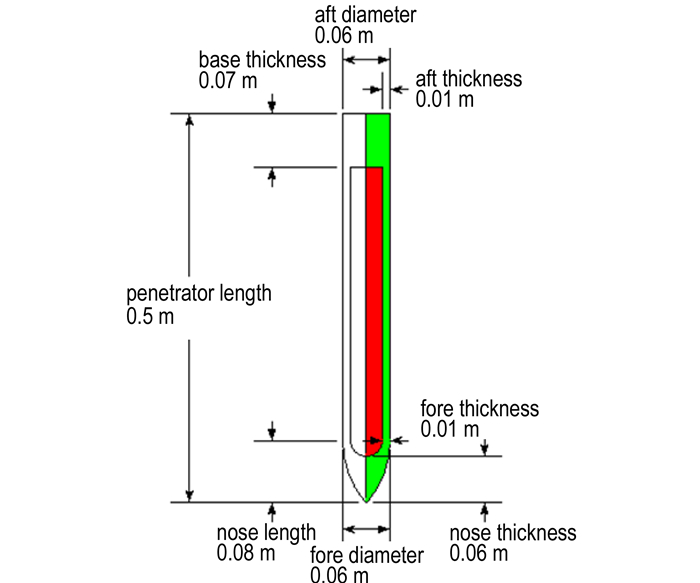
建立二维侵彻混凝土靶板的计算模型如图 10所示。边界条件, 加载条件均为轴对称形式, 为节省计算时间, 建立二分之一模型进行计算, 选取侵彻速度800 m·s-1, 设装药外壁与壳体内壁的摩擦因数为0.03, 考虑界面摩擦生热机制与热传导机制, 初始温度为294 K。弹体尺寸如图 11所示, 侵彻的混凝土靶板厚度为0.5 m。混凝土材料使用HJC本构模型[21], 壳体材料使用Johnson-Cook模型[22]。

|
图 10 弹体-靶板模型 Fig.10 Model of projectile and target |
|
图 11 弹体尺寸 Fig.11 Size of the projectile |
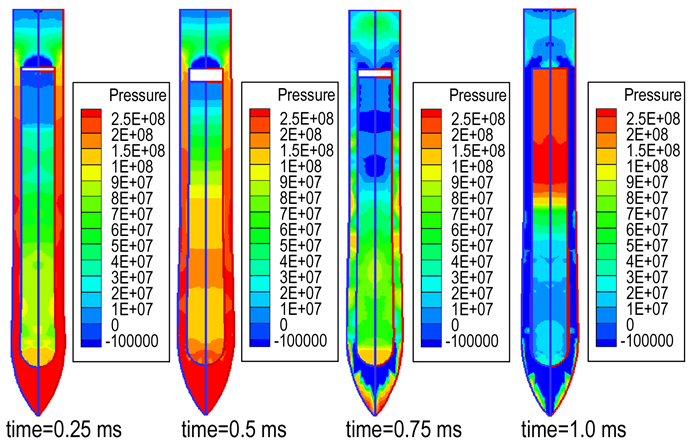
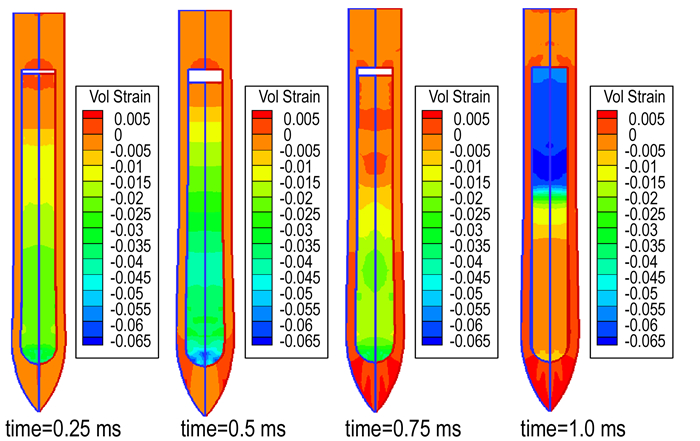
图 12为弹体侵彻过程中装药的压力云图。由图 12可知, 弹体与混凝土靶板初始接触时弹体受到强烈的压缩波作用, 装药头部压力值最大; 随着压缩波的传播, 装药受压区域逐渐变大, 药柱整体长度缩短, 装药尾部与弹体间出现相对位移间隙; 应力波传播至尾部自由端面反射回拉伸波, 在0.75 ms时尾部装药单元变为拉伸状态, 压力为负; 1.0 ms时, 弹体穿出靶板, 装药开始弹性恢复, 由于惯性作用, 装药尾部撞击到了弹体内壁面, 尾部压力迅速升高。图 13是装药的体积应变云图, 由图 13可知, 体积应变最初出现在装药的头部, 随着高压区的扩张, 体积应变从头部扩展到了中部, 因此侵彻后装药前端和中部的密度增大, 而尾部的密度减小, 与实验结果相符[23]。
|
图 12 弹体侵彻过程中压力应变云图 Fig.12 Pressure strain nephograms in the penetration process of projectile |
|
图 13 弹体侵彻过程中体积应变云图 Fig.13 Volume strain nephograms in the penetration process of projectile |
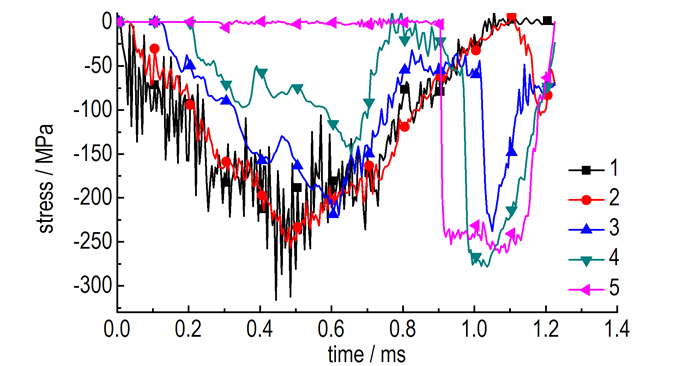
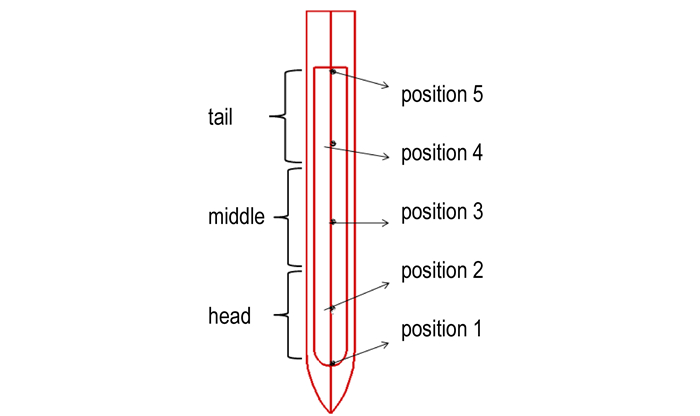
为研究应力波在药柱内的传播规律, 选取了五个位置的单元分析其轴向应力随时间的变化, 如图 14所示, 根据药柱的压力分布云图和体积应变分布云图, 把药柱分为三个部分, 头部初始压缩区, 中部压力扩展区, 尾部撞击高压区, 如图 15所示。
|
图 14 不同位置的轴向应力演化图 Fig.14 Axial stress evolution of different location |
|
图 15 弹体内装药位置示意图 Fig.15 Charge location diagram in projectile |
从图 14可以看出, 初始时刻位置1处单元就受到较大的轴向应力, 随后应力波逐渐传播至位置2、3、4处, 幅值有所衰减; 位置5处单元在0.9 ms时撞击到了壳体内壁面, 突然产生较大的轴向应力, 脉宽0.3 ms, 该应力随后向中部传播, 头部受到的影响较小。
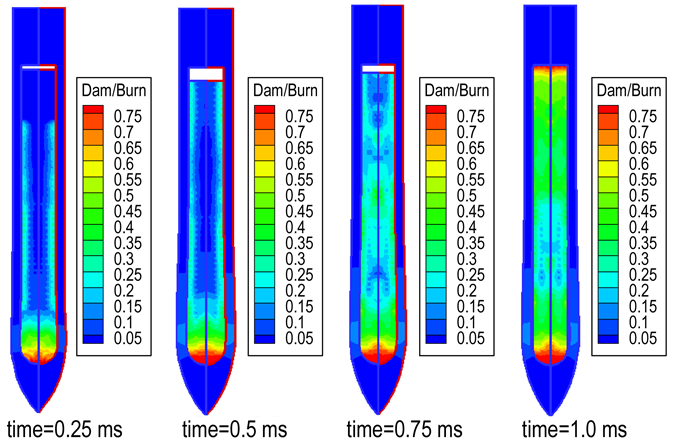
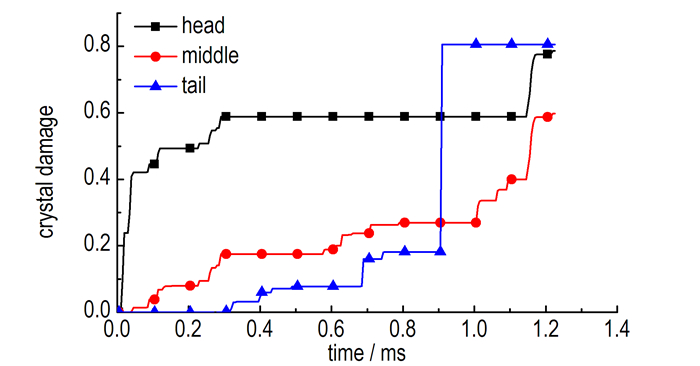
炸药的晶体破碎损伤云图如图 16所示, 头部、中部和尾部的平均损伤程度随时间的变化如图 17所示。由图 16可知, 孔隙压塌损伤与应变率相关, 装药外壁面与壳体内壁面的摩擦作用使得装药外壁面也存在一定程度的晶体破碎损伤, 侵彻初期头部损伤较为严重, 0.4 ms时头部损伤就上升到0.6, 而尾部和中部不超过0.2; 0.9 ms时, 装药尾部受剧烈撞击, 晶体破碎损伤突然加剧, 损伤值为0.8, 由于晶体断裂后, 晶体间的裂纹面容易产生摩擦作用, 在侵彻过程中有可能发生意外点火, 因此装药头部和尾部作为晶体破碎损伤较高的区域应作为重点防护区域。
|
图 16 弹体侵彻过程中晶体破碎损伤云图 Fig.16 Crystal fragmentation damage nephograms in the penetration process of projectile |
|
图 17 不同装药位的晶体压塌损伤演化 Fig.17 Evolution of crystal collapse damage at different location of charge |
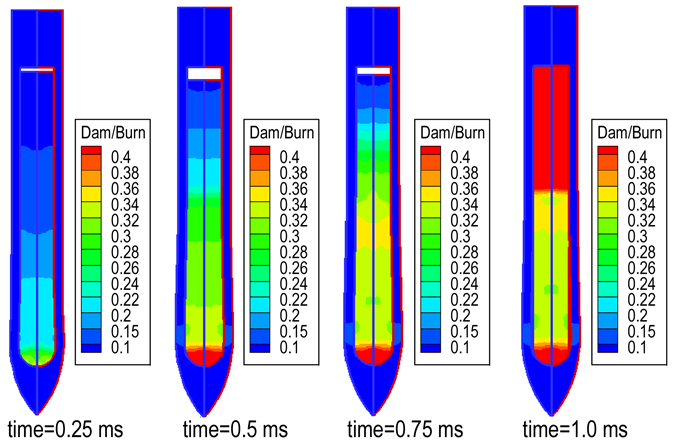
侵彻过程中装药的孔隙压塌损伤分布云图如图 18所示, 该损伤与体积应变相关, 头部和尾部压缩量较大, 孔隙压塌损伤也较大。尾部损伤量最大达到了0.43, 如图 19所示。与陈文[23]等人提出的, 装药头部和尾部出现明显的孔隙压塌和深度裂纹, 密度变化也较大, 而中部损伤较轻的实验结果一致。
|
图 18 弹体侵彻过程中装药孔隙压塌损伤云图 Fig.18 Void collapse damage nephograms of the charge in the penetration process of projectile |

|
图 19 装药孔隙压塌损伤随时间的演化 Fig.19 The evolution of void collapse damage of charge with time |
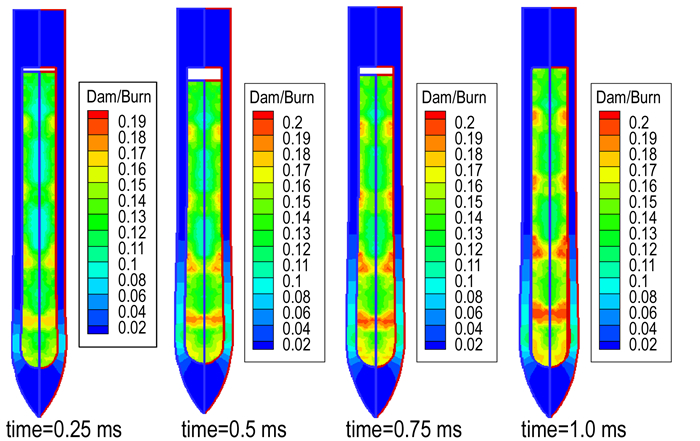
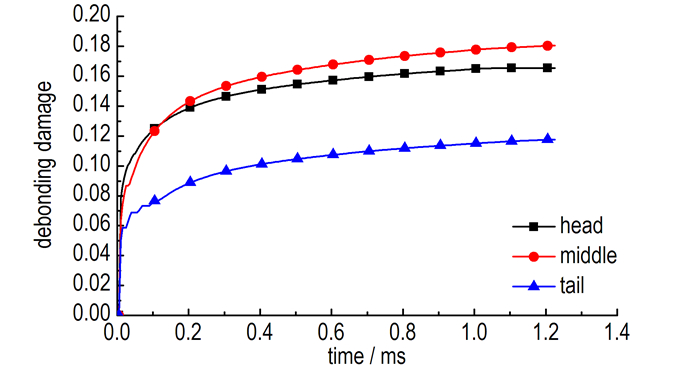
图 20为弹体侵彻过程中粘结剂脱粘损伤云图, 由图 20可知, 当拉伸波传过药柱, 单元处于拉伸状态时, 脱粘损伤开始积累, 由于装药外壁面和壳体的摩擦作用和药柱的惯性作用, 导致粘结剂界面脱粘损伤主要集中在外壁面单元, 并有向装药内部扩散的趋势, 但由于装药在侵彻过程中主要处于受压状态, 因此, 粘结剂界面脱粘损伤不大, ,集中在在药柱中部外壁面, 最大损伤值为0.18(图 21)。
|
图 20 弹体侵彻过程中粘结剂脱粘损伤云图 Fig.20 The debonding damage nephograms of binder in the penetration process of projectile |
|
图 21 粘结剂脱粘损伤随时间演化 Fig.21 The evolution of debonding damage of binder with time |
该粘弹性本构模型的应变率适用范围较广, 涵盖了准静态加载和动态加载, 能描述材料的温度软化、应变率硬化效应和蠕变效应, 亦体现出了材料的拉压不同性特征; 通过计算表明:
(1) 不同的力学环境下, 炸药产生的主要损伤不同, 准静态拉伸过程中, 粘结剂与炸药晶粒间的界面脱粘损伤占主导地位, 炸药晶体的断裂破碎更易发生在较高应变率下, 而炸药晶体间的孔隙压塌则在各种受力环境下均有发生。
(2) 在侵彻过程中, 加载初期炸药装药的头部承受较大的压缩应力, 当应力波传播至尾部反射回拉伸波时, 装药尾部和壳体内表面发生撞击, 迅速形成高压区, 容易发生意外点火。
(3) 装药的粘结剂脱粘损伤较小, 而头部和尾部的晶体破碎损伤和孔隙压塌损伤较为明显。因此, 头部和尾部应作为重点防护区域。
| [1] |
Thompson D G, Wright W J. Mechanical properties from PBX 9501 pressing study[C]//Shock Compression of Condensed Matter-2003: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter. AIP Publishing, 2004, 706(1): 503-506.
|
| [2] |
Gratton M, Gontier C, et al. Mechanical characterisation of a viscoplastic material sensitive to hydrostatic pressure[J].
European Journal of Mechanics Solids, 2009, 28: 935-947. DOI:10.1016/j.euromechsol.2009.03.002 |
| [3] |
Field J E, Swallowe G M, Heavens S N. Ignition mechanisms of explosives during mechanical deformation[C]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1982, 382(1782): 231-244.
|
| [4] |
AntićG, DžingalaševićV. Characteristics of cast PBX with aluminium[J].
Scientific Technical Review, 2006, 56(3-4): 52-58. |
| [5] |
Idar D J, Thompson D G, Gray G T, et al. Influence of polymer molecular weight, temperature, and strain rate on the mechanical properties of PBX 9501[C]//AIP Conference Proceedings, 2002 (2): 821-824.
|
| [6] |
Thompson D G, Idar D J, Gray G T, et al. Quasi-static and dynamic mechanical properties of new and virtually-aged PBX 9501 composites as a function of temperature and strain rate[C]//Proceedings of the 12th International Detonation Symposium. Arlington, VA: Office of Naval Research. 2002: 363-368.
|
| [7] |
Antić G, Rodić V, Borković Z. Influence of content and dispersion of octagene and oxidizer on the mechanical properties of cast aluminized PBX[J].
Scientific Technical Review, LVIII (2), 2008: 51-59. |
| [8] |
Quidot M, Racimor P, Chabin P. Constitutive models for PBX at high strain rate[C]//AIP Conference Proceedings. AIP, 2000, 505(1): 687-690.
|
| [9] |
Richeton J, Ahzi S, Vecchio K S, et al. Influence of temperature and strain rate on the mechanical behavior of three amorphous polymers: characterization and modeling of the compressive yield stress[J].
International Journal of Solids and Structures, 2006, 43(7): 2318-2335. |
| [10] |
Balzer J E, Siviour C R, Walley S M, et al. Behaviour of ammonium perchlorate-based propellants and a polymer-bonded explosive under impact loading[C]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 2004, 460(2043): 781-806.
|
| [11] |
Forrestal M J. Penetration into dry porous rock[J].
International Journal of Solids & Structures, 1986, 22(12): 1485-1500. |
| [12] |
孙宝平, 段卓平, 万经伦, 等. 基于Visco-SCRAM模型的侵彻装药点火研究[J].
爆炸与冲击, 2015, 35(5): 689-695. SUN Bao-ping, DUAN Zhuo-ping, WAN Jing-lun, et al. Investigation on ignition of an explosive charge in a projectile during pentation based on Visco-SCRAM model[J]. Explosive and Shock Waves, 2015, 35(5): 689-695. DOI:10.11883/1001-1455(2015)05-0689-07 |
| [13] |
Gruau C, Picart D, Bouton E, et al. Ignition of a confined high explosive under low velocity impact[J].
International Journal of Impact Engineering,, 2009, 36: 537-550. DOI:10.1016/j.ijimpeng.2008.08.002 |
| [14] |
Bennett J G, Haberman K S, Johnson J N, et al. A constitutive model for the non-shock ignition and mechanical response of high explosives[J].
Journal of the Mechanics and Physics of Solids, 1998, 46(12): 2303-2322. DOI:10.1016/S0022-5096(98)00011-8 |
| [15] |
Dienes J K. Permeability, percolation and statistical crack mechanics[C]//The 23rd US Symposium on Rock Mechanics (USRMS). American Rock Mechanics Association, 1982.
|
| [16] |
Mas E M, Clements B E, Blumenthal W R, et al. A viscoelastic model for PBX binders[C]//AIP Conference Proceedings. 2002(1): 661-664.
|
| [17] |
Chen P, Huang F, Ding Y. Microstructure, deformation and failure of polymer bonded explosives[J].
Journal of Materials Science, 2007, 42(13): 5272-5280. DOI:10.1007/s10853-006-0387-y |
| [18] |
B.E. Clements, E.M. Mas. EA theory for plastic-bonded materials with a bimodal size distribution of filler particles[J].
Modell Simul Mater Sci Eng,, 2004, 12: 407-421. DOI:10.1088/0965-0393/12/3/004 |
| [19] |
Simo J C. On a fully three-dimensional finite-strain viscoelastic damage model: formulation and computational aspects[J].
Computer Methods in Applied Mechanics and Engineering, 1987, 60(2): 153-173. DOI:10.1016/0045-7825(87)90107-1 |
| [20] |
Xiao Y C, Sun Y, Li X, et al. Dynamic mechanical behavior of PBX[J].
Propellants, Explosives, Pyrotechnics, 2016 |
| [21] |
Dancygier A N. Concrete strength effect on penetration and perforation resistance to impact of non-deforming projectiles[C]//International Symposium on Plasticity and Impact Mechanics. 2003: 826-832.
|
| [22] |
Polanco loria M, Hopperstad O S, Borvik T, et al. Numerical predictions of ballistic limits for concrete slabs using a modified version of the HJC concrete model[J].
International Journal of Impact Engineering, 2008, 35(5): 290-303. DOI:10.1016/j.ijimpeng.2007.03.001 |
| [23] |
陈文, 张庆明, 胡晓东, 等. 侵彻过程冲击载荷对装药损伤实验研究[J].
含能材料, 2009, 17(3): 321-325. CHEN Wen, ZHANG Qing-ming, HU Xiao-dong, et al. Experimental study on damage to explosive charge by impact load in the process of penertration[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2009, 17(3): 321-325. |




