固体火箭发动机(SRM)药柱在制造、贮存、运输、点火和飞行过程中, 要承受热应力、冲击、振动、加速度和点火压力等载荷的作用。这些载荷会使药柱内部产生应力和应变, 如果超过其力学性能的允许范围, 将会造成药柱的破裂、变形和药柱及壳体粘结界面的脱粘, 从而导致SRM工作性能严重恶化, 甚至整个发动机炸毁[1]。由此可见, SRM的结构可靠性很大程度上受到药柱结构完整性的影响。而固体推进剂力学性能和本构模型的研究是开展药柱结构完整性分析的基础。固体推进剂的力学性能明显受到外界温度、加载应变率和加载方式的影响[2], 因此, 进行不同加载条件下固体推进剂力学性能和本构模型的研究对于指导药柱的结构设计和确保SRM的正常工作等具有重要的意义。
固体推进剂的力学性能研究以实验研究为基础, 重点是分析不同加载条件下的曲线特性和获取关键性力学性能参数, 并讨论这些参数随加载条件的变化规律, 最后, 通过数据分析和本构模型的构建对更广加载范围内固体推进剂的力学性能进行预测。目前, 国内外的研究者已经基于各种实验装置和测试方法对固体推进剂的力学性能开展了较为广泛的研究, 并构建了相应的本构模型, 但是, 由于固体推进剂力学性能的复杂性, 已经开展的有关研究与实际需求还存在较大的差距。因此, 本文从力学性能的实验测试方法、力学性能参数的确定以及本构模型的构建三个方面对固体推进剂力学性能和本构模型的研究进展进行归纳和总结, 并就研究中存在的不足进行讨论和分析。
2 力学性能的实验测试方法根据不同目的, 固体推进剂的力学性能实验可以分为两大类, 一类是为推进剂配方研究和质量控制服务, 一类是为SRM药柱结构完整性分析提供数据支撑, 本文主要综述后者的研究。目前, 针对固体推进剂的力学性能实验研究, 按应变率范围划分, 其主要测试方法有准静态力学性能实验和动态力学性能实验。
2.1 准静态力学性能实验研究 2.1.1 准静态单轴拉压力学性能实验基于常规材料试验机开展准静态(< 1 s-1)不同温度和不同老化时间下的定应变率单轴拉伸实验、应力松弛实验和蠕变实验, 是研究固体推进剂力学性能的主要手段。目前, 针对这些广泛应用的力学性能实验, 国内外已经建立了较为完善的标准, 并对实验件的具体尺寸等有非常详细的规定, 比如国外早在1957年就建立的JANNAF标准[3], 国内于2005年重新修订后颁布的GJB 770B-2005标准(测试方法413)[4]和QJ 2328A-2005标准[5]。虽然, Blumenthal等[6]基于圆柱形实验件开展了准静态不同温度条件下固体推进剂的单轴压缩力学性能实验, 但是, 目前针对固体推进剂压缩力学性能实验的标准还十分匮乏, 在实际实验中多参考其它材料的测试方法, 比如GJB 770B-2005标准中415.1提出的针对火药的准静态单轴压缩力学性能测试方法[4]。此外, 圆柱形实验件的长径比对固体推进剂的压缩实验结果有非常明显的影响, 但是, 目前针对该参数还没有统一标准。Iwamoto等[7]指出, 应变率较低时压缩实验件的长径比一般可选为1~2, 而高应变率加载时, 实验件的长径比可选为0.5~1。
2.1.2 准静态双轴拉伸力学性能实验目前, 针对固体推进剂的双轴力学性能实验测试方法, 还没有很完善的标准, 国内外研究者主要基于板条实验件[8-9]和十字形实验件[10-13]开展准静态双轴拉伸条件下固体推进剂的力学性能实验研究。由于板条实验件能够较好地模拟SRM药柱内孔表面在硫化降温等载荷下的双轴应力状态, 因此, 其自1960年以来在研究固体推进剂的双轴拉伸力学性能时得到了最为广泛的应用。同时, 基于板条双轴拉伸力学性能实验获得的数据也已经用于SRM药柱的结构完整性分析中[8]。但是, 由于板条双轴拉伸力学性能实验只能在小应变弹性变形范围内于实验件中心部位近似获得2:1的双轴拉伸[9], 因此, 近年来, 张丽华[10]、强洪夫[11]、贾永刚[12]和Jalocha[13]等逐步基于十字形实验件开展固体推进剂的双轴拉伸力学性能实验研究, 其典型实验件形状和实验装置如图 1所示。虽然, 这些十字形实验件在形状和尺寸上有差别, 但中心部位多具有与哑铃形实验件一样的纵向截面。

|
图 1 固体推进剂十字形双轴拉伸实验件与试验机的装配图[11-13] Fig.1 Cruciform shape biaxial tensile sample of solid propellant with the testing machine[11-13] |
目前, 基于十字形实验件的固体推进剂的准静态双轴拉伸力学性能实验, 按实验装置的类型又可以分为两大类, 即分别采用单轴拉伸试验机和双轴拉伸试验机的测试方法。其中, 张丽华[10]结合单轴拉伸试验机和自主设计的特殊实验夹具成功开展了双铅-2固体推进剂的双轴力学性能实验, 发现, 由于固体推进剂的力学各向异性, 使得各个方向的剖截试样在双轴拉伸时表现的不同。基于双轴拉伸试验机, 强洪夫等[11]采用中心区减薄的十字形实验件(图 1a)、贾永刚等[12]采用中心区减薄与臂上开槽相结合的十字形实验件(图 1b), 分别开展了复合固体推进剂的双轴拉伸力学性能实验, 研究发现, 固体推进剂具有明显的双向弱化效应。由于固体推进剂具有低模量和低强度等物理特性, 以及对固体推进剂进行雕刻加工具有危险等级高和工艺复杂等原因, Jalocha等[13]认为, 中心减薄和臂上开槽等措施并不能很好地提高十字形实验件双轴拉伸力学性能实验的可靠性。因此, 基于双轴拉伸试验机, Jalocha等[13]采用扩大圆弧段半径的无开槽平板十字形实验件成功开展了复合固体推进剂的双轴拉伸力学性能实验(图 1c), 并分析了双轴拉伸应力状态下预应变对固体推进剂非线性粘弹性的影响。
2.1.3 准静态三轴拉压力学性能实验目前, 针对三轴应力状态下固体推进剂的准静态拉压力学性能研究, 国内外研究者主要开展了基于圆形薄片的“扑克筹码片”实验[14]、基于厚圆盘的径向压缩实验[15]、基于圆管状实验件的实验[16]以及围压实验[17-19]。由于后两种实验能够更好地模拟点火增压环境下固体推进剂的力学性能和有效分析SRM药柱的结构完整性, 其在工程研究中得到较为广泛的应用。Sanal Kumar等[16]通过不同应力状态下的准静态松弛实验发现, 在较短松弛时间内, 应力状态并不影响固体推进剂的松弛模量, 但随着时间的增加, 基于圆管状实验件获得的松弛模量比同等实验条件下板条拉伸实验获得的松弛模量高18%~30%, 比单轴拉伸条件下获得的松弛模量高25%~43%。Liu[17]对围压下固体推进剂填充颗粒周围的应力状态的分析表明: (1)无论在环境压强还是外加压强下, 颗粒的表面都存在较高的三轴拉伸应力; (2)在环境压强下, 拉伸应力包围高三轴拉应力区域, 而在外加压强下包围着高三轴拉应力区域的是压应力, 损伤的萌生和演化被抑制, 材料具有更高的强度和模量。张亚[18]开展了室温不同老化时间四种围压条件下端羟基聚丁二烯(HTPB)固体推进剂的准静态力学性能实验, 研究发现, 围压的存在有利于固体推进剂的长期贮存。Zhang等[19]基于围压实验分析了不同压强对三轴应力状态下改性双基固体推进剂力学性能的影响, 并构建了相应的强度准则。
2.1.4 准静态断裂力学性能实验基于常规材料试验机, Liu等[20-24]采用中间穿透型平板裂纹实验件广泛开展了准静态拉伸条件下固体推进剂的断裂力学性能实验, 获得了温度、应变率、实验件厚度、裂纹宽度、应力状态以及老化时间等对裂纹扩展的影响, 并构建了裂纹扩展的模型。
2.2 动态力学性能实验研究 2.2.1 动态单轴拉压力学性能实验目前, 由于实验装置本身特性的限制, 动态加载条件下固体推进剂的力学性能实验研究主要基于分离式Hopkinson压杆(SHPB)技术, 但需要采用波形整形技术、在入射杆端部涂抹润滑剂以及改变应变片材料等措施对SHPB装置进行改进。Sun等[25-26]在SHPB装置上增加保温装置, 开展了不同温度高应变率(>102 s-1)条件下固体推进剂的单轴压缩力学性能实验。
为研究动态单轴拉伸条件下固体推进剂的力学性能, 强洪夫等[27-29]用新型高应变率液压伺服试验机和自主设计的实验夹具成功开展了1~102 s-1应变率范围内HTPB固体推进剂的力学性能实验, 其实验装置如图 2所示, 研究发现, 在1~102 s-1应变率范围内, 固体推进剂具有明显区别于准静态和高应变率下的力学性能。图 2所示的实验装置具有以下两方面的优点: (1)能够较快地将实验件安装在试验机上, 节省了大量的实验准备时间, 这在进行大量实验时非常关键; (2)由于支撑杆的作用, 避免了拉伸前实验夹具对实验件造成损伤, 提高了实验的可靠性。

|
图 2 HTPB固体推进剂拉伸实验件和新设计铝制夹具与试验机的装配图[29] Fig.2 HTPB propellant tensile sample and the new designed aluminum gripping jaws with the testing machine[29] |
为研究高应变率加载条件下固体推进剂的断裂力学性能, 斯坦福研究院(SRI)利用飞片对含环四次甲基四硝铵(HMX)的复合改性双基固体推进剂的断裂行为进行了实验研究, 并在断裂动力学研究基础上建立了固体推进剂的断裂与破碎模型, 最终成功地应用于模拟固体推进剂受冲击实验[30]。但是, SRI建立的模型比较复杂, 需确定的实验参数较多, 对回收实验件需进行精细的细观测试, 给实际应用带来了较大困难。黄风雷等[31]基于飞片撞击实验设计了平板撞击实验, 很好地研究了复合固体推进剂的动态断裂力学性能, 并对推进剂断裂后发生的层裂现象进行了分析。常新龙等[32-33]采用中心直裂纹圆盘实验件, 在改进的SHPB装置上成功开展了不同温度冲击载荷下固体推进剂的动态断裂特性与破坏机理研究, 并构建了断裂强度因子的主曲线, 该研究为开展高应变率下固体推进剂的断裂力学性能实验提供了新思路。
2.3 当前研究中存在的不足和展望目前, 固体推进剂的力学性能实验测试方法研究, 主要存在以下两方面的不足:
(1) 动态加载条件下固体推进剂的力学性能实验测试方法研究还十分匮乏:首先, 虽然强洪夫等[27-29]成功开展了应变率在102 s-1以内的固体推进剂动态单轴拉伸力学性能实验研究, 但是, 缺乏更高应变率条件下的测试方法; 其次, 公开文献中很少看到有关中应变率(1~102 s-1)范围内固体推进剂的动态单轴压缩力学性能实验研究; 第三, 多轴应力状态下固体推进剂的动态拉压力学性能实验研究几乎没有开展; 第四, 缺乏有效开展中应变率范围内固体推进剂动态断裂力学性能实验的测试方法。
(2) 有效开展多轴应力状态下固体推进剂的力学性能实验研究还存在相当大的难度。首先, 固体推进剂双轴拉伸力学性能实验的实验件破坏部位离散性较大, 这严重限制了实验数据的可靠性; 其次, 缺乏有效判断多轴应力状态下固体推进剂力学性能实验结果准确性的手段; 第三, 固体推进剂的双轴压缩和双轴拉-压等力学性能实验几乎没有开展。
由于固体推进剂属于应变率敏感性材料, 因此, 针对复合材料、炸药和脆性材料等开展的力学性能实验可为固体推进剂力学性能实验的研究提供借鉴。
(1) 借鉴基于分离式Hopkinson拉杆(SHTB)技术的高应变率单轴拉伸力学性能实验。自1960年以来, Harding等[34-36]相继提出了反射式、直接撞击式和直接释放式Hopkinson拉杆技术, 其中, Ogawa等[35]提出的方法在研究材料的高应变率单轴拉伸力学性能时得到了最为广泛的应用。2009年前后, 陈荣等[37]提出了拉压通用型Hopkinson技术, 并研究了高聚物粘结炸药(PBX)的动态单轴力学性能。
由于固体推进剂具有低模量和低阻抗等特性, 因此, 采用SHTB装置进行固体推进剂的高应变率单轴拉伸力学性能实验, 需要特别注意以下三点: ①采用波形整形技术、降低输出杆波阻抗和改变应变片材料等措施提高实验的可靠性; ②分析入射波、反射波和投射波的信号, 验证实验过程中应变率的稳定性; ③选择合适的实验件安装方法。当前基于SHTB装置开展材料的高应变率单轴拉伸力学性能实验时, 实验件的安装方法主要有三种, 分别是胶粘接、螺纹装配和压板压紧。但是, 这三种方法都存在一定的不足, 例如胶粘接方法容易因为粘接不牢固而在粘接部位断开, 螺纹装配方法造成实验件加工工艺复杂, 并容易在螺纹连接处影响波的传播。Owens等[38]基于SHTB装置开展颗粒增强复合材料的高应变率单轴拉伸力学性能实验时的实验件安装方法可以为该问题的解决提供借鉴, 图 3为实验装置示意图和实验件安装图。
(2) 通过对准静态材料试验机和传统SHPB装置进行改进, Othman[39]、Song等[40]分别开展了中应变率条件下材料的单轴力学性能实验研究, 其测试方法可为固体推进剂的力学性能实验研究提供借鉴。
(3) 基于准静态单轴材料试验机, Brieu[41]、Kossa等[42]分别采用专门设计的实验夹具成功开展了橡胶类材料的双轴拉伸力学性能实验和聚合物泡沫的双轴压缩力学性能实验, 其实验装置如图 4所示。唐维等[43]分别基于端部约束压溃实验和端部约束拉溃实验开展了某TATB基PBX的三轴压缩和三轴拉伸力学性能实验, 实验中基于准静态单轴材料试验机通过调节边界条件实现三轴应力状态下的拉压实验。Bailly等[44]基于SHPB装置成功开展了高应变率条件下复合材料的三轴压缩力学性能实验。Brieu等[41-44]的研究均基于单轴实验装置开展, 因此, 将其测试方法与高应变率单轴材料试验机或SHPB装置等有效结合, 并通过设计合适的实验件, 具有开展动态加载条件下固体推进剂多轴力学性能实验的潜力。

|
图 4 基于单轴试验机的双轴拉压力学性能实验装置[41-42] Fig.4 Biaxial tensile and compressive experimental apparatus based on the uniaxial testing machine[41-42] |
总结国内外的研究, 发现, 不同加载条件下固体推进剂的应力-应变曲线具有以下特点:
(1) 由于相对其它含能材料具有更高质量分数的粘合剂组分, 固体推进剂一般能够发生大变形, 并且呈现出明显的粘弹性特性, 甚至部分推进剂在压缩时还具有粘塑性。此外, 随温度的降低和应变率的升高, 固体推进剂的应力-应变曲线特性可能会变得更加复杂, 呈现出与常规曲线特性不同的规律。
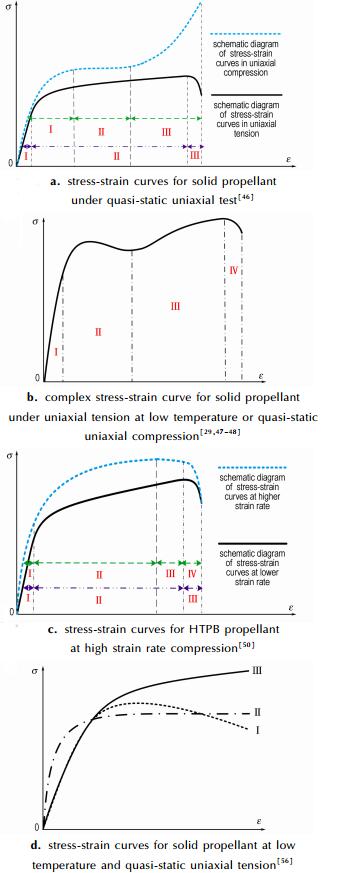
(2) 在准静态单轴加载条件下, 固体推进剂的应力-应变曲线一般呈现三段特性, 如图 5a所示。其中, 在单轴拉伸条件下, 曲线表现出明显的弹性段、“脱湿”损伤段和破坏段三段变化规律。Francis等[45]指出, “脱湿”损伤段是推进剂变形中微裂纹扩展至颗粒/基体界面, 使得颗粒与基体分离, 造成推进剂承载能力降低而形成的, 这同样也是拉伸应力-应变曲线呈现非线性的主要原因。在单轴压缩条件下, 推进剂曲线表现出明显的线弹性压缩段、应力硬化段和破坏失稳段三段变化规律。常新龙等[46]指出, 应力硬化段是推进剂内部产生宏观裂纹并且不断扩展, 从而造成推进剂发生塑性变形而形成的。但Landsem等[47]在进行无烟高燃速复合固体推进剂的低温准静态拉伸力学性能实验时发现, 推进剂的应力-应变曲线呈现出如图 5b所示的多段特性, 即初始线性段、屈服与应变软化段、应变强化段和破坏段。此外, 胡少青等[48]开展双基固体推进剂的准静态压缩力学性能实验时, 同样发现了如图 5b所示的多段特性, 而且随加载温度的降低和应变率的升高, 该特性愈加明显。
|
图 5 不同加载条件下固体推进剂的应力-应变曲线特性[29, 46-48, 50, 56] Fig.5 The characteristics of stress-strain curves for solid propellants under various test conditions[29, 46-48, 50, 56] |
(3) 在高应变率单轴压缩加载条件下, 应力-应变曲线一般也呈现出三段特性。Ho等[49]在对HTPB固体推进剂进行不同温度下的高应变率(103~104 s-1)压缩加载时发现, 在所有温度下推进剂的应力-应变曲线特性一致, 即均具有线弹性压缩段、屈服发生后的延性变形应力硬化段和破坏失稳段。同时, Ho指出, 在线弹性压缩段, 推进剂内部已经有了微裂纹和孔洞, 而在应力硬化段, 推进剂可能同时发生了粘弹性变形和粘塑性变形, 并且裂纹发生了进一步扩展, 甚至可能在该阶段还有二次损伤机理的发生。赖建伟[50]在对HTPB固体推进剂进行低温高应变率(7×102~2×103 s-1)条件下的单轴压缩实验时发现, 其应力-应变曲线特性在低温不同应变率下呈现出不同的变化规律, 如图 5c所示, 即在较低应变率下, 应力-应变曲线呈现与准静态下一致的三段变化规律特性, 而在较高应变率下, 则呈现出四段变化规律的多段特性。王哲君等[29]对HTPB固体推进剂进行1~102 s-1应变率范围的动态单轴拉伸实验时发现, 其应力-应变曲线特性在不同温度和不同应变率下呈现出不同的变化规律, 即在常温下, 推进剂变形时仍呈现出三段变化规律的特性, 而在低温较高应变率下, 则呈现出如图 5b所示的多段特性, 且随温度的降低和应变率的升高, 该多段特性更容易出现。
一般认为, 不同加载条件下固体推进剂的应力-应变曲线特性与推进剂本身特性的改变和内部损伤的发生密切相关, 同时受推进剂配方等的影响。因此, 不同加载条件下固体推进剂具有不同的应力-应变曲线特性可能是因为:
(1) 室温, 较高应变率单轴拉伸条件下, 固体推进剂内部的裂纹来不及向颗粒/基体界面扩展, 因而推进剂变形时有更大的伸长率[51]。低温条件下, 固体推进剂变硬变脆, 因而具有更高的强度和模量, 但伸长率显著降低[52]。Landsem等[53]在进行无烟高燃速复合固体推进剂的低温准静态单轴拉伸实验时发现, 随温度的降低, 推进剂的断裂伸长率明显升高, 具有反常现象, 该现象在部分硝酸酯增塑的聚醚(NEPE)高能固体推进剂的低温准静态单轴拉伸实验时也有出现。Shekhar等[54]将NEPE固体推进剂出现的这种反常现象归结为应变诱导结晶, 而Landsem等[53]则认为, 粘合剂组分聚叠氮缩水甘油醚-丁基硝氧乙基硝铵(GAP-BuNENA)在低温下表现出的半晶质特性是导致无烟高燃速复合固体推进剂出现这种反常现象的原因。
(2) Landsem等[47]认为, 低温准静态单轴拉伸条件下无烟高燃速复合固体推进剂应力-应变曲线上的应变软化段与其内部“脱湿”的出现紧密相关, 因为为提高燃速, 推进剂内部添加了粒度更小的高氯酸铵(AP)颗粒, 而细小颗粒的添加降低了固体颗粒与基体之间的粘结强度, 使推进剂更容易在较小应变处发生“脱湿”, 从而降低应力值。侯林法[55]从固化交联和界面粘结性能等方面对准静态单轴拉伸条件下固体推进剂的应力-应变曲线特性进行了解释, 其指出, 在低温下拉伸时, NEPE高能固体推进剂应力-应变曲线上出现的多段特性是推进剂在低温下发生结晶而造成的, 如果粘合剂体系不结晶或存在界面粘结失效, 则该多段特性会消失。胡少青等[48]认为, 准静态单轴压缩条件下双基固体推进剂应力-应变曲线上应变软化段的出现主要是推进剂在较高应变率下发生了塑性变形, 且内部产生的热量不足以扩散至周围环境中, 从而造成应力下降而形成的。赖建伟[50]认为, 低温高应变率单轴压缩条件下HTPB固体推进剂应力-应变曲线的多段特性与推进剂内部发生更严重的固体颗粒破裂有关。王哲君等[29]通过对动态单轴拉伸后HTPB固体推进剂的断面形貌进行电镜扫描发现, 低温下推进剂的损伤机理是AP颗粒发生穿晶断裂。因此, 低温较高应变率下推进剂应力-应变曲线的多段特性也与推进剂内部发生更严重的固体颗粒破裂有关, 同时, 推进剂玻璃化温度的变化也会对应力-应变曲线特性产生影响。而杨凤林等[56]则将低温准静态单轴拉伸条件下固体推进剂的曲线特性划分为三种不同的情况(图 5d), 并运用模糊群子理论对各种曲线特性进行了分析, 认为, 固体推进剂曲线特性可由屈服因素和阻碍形变因素的主次对比来决定。
Renganathan等[57-58]对准静态加载条件下HTPB固体推进剂的板条双轴拉伸实验结果和老化后单轴拉伸实验结果进行分析发现, 推进剂的应力-应变曲线具有和常规准静态单轴拉伸实验时一致的特性, 只是强度和伸长率的值有所不同。因此, 本文不再对这些加载条件下固体推进剂的应力-应变曲线特性进行单独阐述。
3.2 典型力学性能参数的确定要研究不同加载条件下固体推进剂的力学性能, 并为本构模型构建和SRM药柱的结构完整性分析提供数据支撑, 则一般要确定推进剂的模量、强度、伸长率以及屈服点或“脱湿”点等力学性能参数。目前, 国内外研究者已经针对部分固体推进剂力学性能参数的确定方法给出了明确的标准, 比如单轴拉伸初始模量、单轴抗拉强度和单轴拉伸伸长率等[4], 但其它部分典型力学性能参数的确定还存在较大的难度。因此, 本文主要基于国内外研究者在相关问题上的研究成果, 就以下三个方面的内容进行简单阐述:
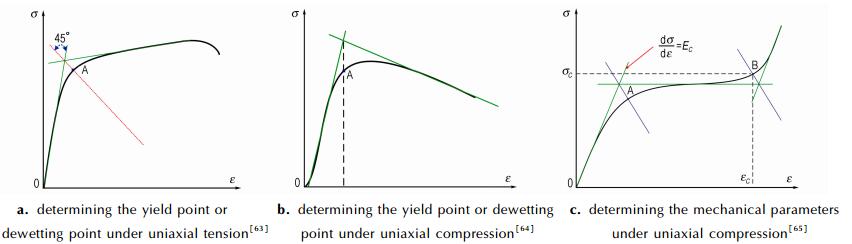
(1) 屈服点或“脱湿”点的确定。国内外研究者一致认为, 固体推进剂应力-应变曲线上的屈服点是推进剂具有非线性粘弹性的起点, 或是固体推进剂发生“脱湿”损伤的起始点, 该点的准确确定对于研究固体推进剂的力学性能等具有重要的意义。自1970年以来, 国内外研究者采用了各种方法来确定固体推进剂变形时的屈服点或“脱湿”点, 这些方法按思想的不同, 可大致分为:实验观测的方法、应力-应变曲线作图的方法和数值计算的方法。①Nevière等[59]认为, 固体推进剂发生“脱湿”后, 其内部会产生微孔洞和微裂纹, 进而引起推进剂体积的膨胀, 这种膨胀可以通过气体或液体膨胀计测量, 因而可以基于该思想确定推进剂变形时的“脱湿”点。李敬明等[60]采用原位扫描电镜实时观测不同拉伸变形阶段NEPE固体推进剂的细观损伤情况, 进而确定推进剂单轴拉伸变形时的“脱湿”点。除此之外, Darwell等[61]认为, 固体推进剂的泊松比与其内部的损伤情况紧密相关, 可以通过分析不同变形时刻推进剂的泊松比变化, 进一步确定“脱湿”点。其中, 泊松比可以根据定义通过计算得到, 而变形过程中不同方向上的位移则可以通过引伸计测量或散斑高速摄像观察的方法获得[62]。②Sun[25]、张建彬[63]、Lieb[64]和张晓军[65]等认为, 应力-应变曲线特性能够间接反映不同变形阶段固体推进剂的内部损伤情况, 因而可以直接采用基于应力-应变曲线作图的方法来确定推进剂变形时的屈服点或“脱湿”点。其中, Sun等[25]直接采用单轴压缩变形时应力-应变曲线上应变软化之前的峰值点作为复合改性双基固体推进剂的屈服点, 而其他研究者则采用如图 6所示的作图法获得相应的屈服点或“脱湿”点(图 6中点A)。其中, 图 6a为拉伸加载条件下屈服点或“脱湿”点的确定, 图 6b和图 6c为压缩加载条件下屈服点或“脱湿”点的确定。③ Gazonas等[66]认为, 固体推进剂单轴压缩变形时, 其最大应力值或屈服点位于推进剂快速失去维持压缩变形能力的临界点, 而该临界点可以通过求应力对时间的二次偏导数获得, 但前提是通过唯象的方法拟合得到应力随时间变化的关系式。
|
图 6 确定固体推进剂力学性能参数的应力-应变曲线示意图[63-65] Fig.6 Schematic diagram of stress-strain curves for solid propellant determining the mechanical parameters[63-65] |
(2) 压缩加载条件下力学性能参数的确定。①压缩模量的确定。虽然, 准静态条件下固体推进剂的压缩模量可以基于变形初期的线性段确定, 但基于SHPB装置进行高应变率压缩加载时, 由于变形初期应变率的不稳定性, 准确获得压缩模量比较困难。尽管Naik等[67]指出, 可以首先对高应变率压缩条件下固体推进剂的应力-应变曲线进行光滑处理, 然后基于应变率达到稳定之前的应力-应变曲线的线性段的延伸线来确定压缩模量, 但实际可操作性不强。②压缩强度的确定。由于一般情况下固体推进剂压缩变形时, 其应力-应变曲线上并不出现最大应力值, 尤其是复合固体推进剂, 因此, 有效确定固体推进剂的压缩强度也比较困难。Ouelleta等[68]指出, 准静态压缩变形时, 聚合物材料的应力一般会在50%名义应变附近发生明显的变化, 即预示着材料内部发生了明显的损伤, 因而可以将相应应变处的应力作为聚合物材料的压缩强度。强洪夫[69]、张亚等[18]均基于上述思想进行了室温准静态条件下HTPB固体推进剂压缩强度的应变率敏感性分析。而张晓军等[65]则基于图 6c所示的作图法获得了准静态加载条件下HTPB固体推进剂的压缩强度σC(点B对应的应力)和对应的压缩应变εC, 并分析了温度和应变率对压缩强度的影响。在研究准静态压缩条件下三元乙丙(EPDM)橡胶的力学性能时, 张中水等[70]同样采用了图 6c所示的方法。
(3) 剪切模量的确定。剪切模量对粘弹性材料力学性能的研究十分重要, 其一般通过弹性模量和泊松比求得, 但该方法在计算时具有较大的累积误差。Deng等[71]基于Knauss等[72]的研究指出, 可以利用改进型Arcan夹具对蝶形HTPB固体推进剂实验件进行剪切实验(图 7), 获得不同剪切角下的应力-应变关系, 进而求得剪切模量。

|
图 7 固体推进剂变角剪切力学性能实验装置[71] Fig.7 Shear experimental apparatus for solid propellant with alterable directions[71] |
目前, 针对不同加载条件下固体推进剂力学性能参数确定方面的研究, 主要存在以下三个方面的不足:
(1) 已经开展的相关研究主要是基于常规情况下的分析和讨论, 针对固体推进剂复杂应力-应变曲线特性的分析和力学性能参数的确定还存在较大的难度, 亟待通过借鉴其它非金属材料的分析方法来开展相应的研究, 比如图 6所示的力学性能参数确定方法就很难适用于图 5b所示的推进剂应力-应变曲线。
(2) 针对常温准静态加载条件下固体推进剂发生“脱湿”和基体撕裂形式的损伤研究较多, 缺乏对动态加载条件下或低温与动态加载双重作用下固体推进剂损伤形式的深入研究, 而对这些损伤的深入研究不仅有利于研究者全面认识不同加载条件下固体推进剂的曲线特性和力学性能, 而且有助于分析诸如点火冲击条件下SRM药柱的结构完整性。此外, 针对动态加载条件下固体推进剂的损伤观测和分析的手段还比较缺乏, 随着高速摄像技术和散斑分析方法的不断完善, 可以为该问题的解决提供有效的方法。
(3) 缺乏针对不同应力状态下固体推进剂力学性能参数相互之间关系的讨论和分析, 比如单轴拉伸与单轴压缩力学性能参数之间的关系, 双轴拉伸与单轴拉伸力学性能参数之间的关系。虽然, 强洪夫[11]、张晓军[65]和Ren等[73]在该方面进行了初步的研究, 但仍与实际需求相差较大。由于压缩力学性能实验相对单轴拉伸和双轴拉伸力学性能实验更容易开展, 如果建立了不同应力状态下固体推进剂力学性能参数之间的关系, 则可以基于更少的实验对固体推进剂的力学性能进行预估, 具有可观的经济效益。
4 本构模型的构建 4.1 固体推进剂本构模型研究新进展针对固体推进剂在不同加载条件下的变形, 国内外研究者提出了众多的本构模型, 由于篇幅限制, 本文主要阐述2002年之后固体推进剂非线性粘弹性本构模型研究的新进展。这些本构模型按照描述的固体推进剂变形的应变率范围划分, 主要包括:
4.1.1 准静态加载下的非线性粘弹性本构模型准静态(< 1 s-1)加载下的固体推进剂非线性粘弹性本构模型。主要包括在线粘弹性本构模型的基础上考虑损伤演化的非线性粘弹性本构模型和基于模型理论的非线性粘弹性本构模型。第一类本构模型应用最为广泛, 在本文中将其称为含损伤的积分型非线性粘弹性本构模型。
(1) 含损伤的积分型非线性粘弹性本构模型, 其重点是采用某个变量的变化来描述推进剂变形时的损伤演化, 进而获得损伤函数。目前, 主要采用细观和宏观的方法来构建损伤函数。
细观方法构建损伤函数, 主要是通过计算机断层扫描(CT)、声发射测试或X射线观察等手段分析固体推进剂变形时由于“脱湿”等损伤造成的微裂纹变化情况, 然后采用声发射能量或空穴率等参量描述损伤的演化。2002年前后, 阳建红等[74]利用声发射测试方法对准静态单轴拉伸条件下HTPB固体推进剂变形时的损伤破坏过程进行了详细的分析, 然后采用声发射能量分布作为表征推进剂损伤的特征参量, 最终构建了HTPB固体推进剂的含损伤的积分型非线性粘弹性本构模型。2003年, 彭威等[75]建立了包含基体的粘弹性效应、颗粒的增强效应以及界面“脱湿”微裂纹损伤效应的复合固体推进剂非线性粘弹性本构模型。2008年, Xu等[76]基于复合材料均匀化理论, 提出了以空穴率为参量的含损伤的积分型非线性粘弹性本构模型, 并通过准静态加载条件下固体推进剂的松弛实验和单轴拉伸实验确定了所建本构模型中的参数值。
宏观方法构建损伤函数, 其思想是直接采用宏观物理量的变化来描述固体推进剂变形时的损伤演化, 该宏观物理量可以是专门选定的内变量或推进剂的弹性模量等参量, Schapery等[77]构建的本构模型就是采用内变量变化构建含损伤的积分型非线性粘弹性本构模型的典型代表。2012年, 孟红磊等[78]采用累积损伤的概念获得了单一内变量变化的损伤函数, 并最终在Schapery本构模型的基础上构建了描述准静态单轴拉伸条件下双基固体推进剂变形的非线性粘弹性本构模型。2014年, 基于Schapery本构模型, Xu等[79]采用单一内变量的含损伤的积分型非线性粘弹性本构模型描述了准静态单轴拉伸条件下HTPB固体推进剂的变形, 但损伤函数的形式明显区别于孟红磊等的研究。2014年, 为描述准静态拉伸加载条件下HTPB固体推进剂的变形, 姚东等[80]构建了考虑应力状态的含损伤的积分型非线性粘弹性本构模型, 模型中以宏观弹性模量的变化来反映推进剂变形中损伤的发生与演化, 而假定泊松比为定值。
(2) 聚合物材料的力学性能可以采用表征线弹性力学性能的弹簧元件和表征粘性流体的牛顿粘壶的不同组合来描述, 该类模型称为基于模型理论的粘弹性本构模型。近年来, 部分研究者基于该思想, 通过改变模型参数的表达形式, 构建了固体推进剂的非线性粘弹性本构模型。2006年, Matheson等[81]采用与时间相关的剪切模量替代基本Maxwell模型中的参量, 提出了含损伤的粘弹性本构模型, 模型中的参数是时间和损伤的函数。2012年, Shekhar等[82]将Maxwell本构模型中的弹性模量和粘性系数表征为应变率的函数, 构建了描述准静态单轴拉伸条件下铸造双基固体推进剂和复合固体推进剂变形行为的非线性粘弹性本构模型。
4.1.2 高应变率加载下的非线性粘弹性本构模型国内外研究者主要采用朱-王-唐(ZWT)本构模型[83]、粘-超弹性本构模型以及唯象型本构模型描述高应变率(> 102 s-1)加载条件下固体推进剂的变形, 下文将按照应用的广泛程度依次对这些本构模型进行阐述。
(1) 国内研究者广泛采用ZWT本构模型来描述高应变率单轴压缩条件下固体推进剂的变形。2012年, 王蓬勃等[84]采用ZWT本构模型描述了双基固体推进剂在高低应变率下的单轴压缩变形, 比较预测应力值与实验数据发现, 不考虑损伤的原始ZWT本构模型只能有效描述低应变率、应变范围在2%以内的实验结果, 高应变率下可描述应变到5%时的推进剂变形。2013年, 孙朝翔等[85]采用2006年王礼立等[86]构建的考虑损伤的改进型ZWT本构模型, 描述了高应变率单轴压缩条件下双基固体推进剂的变形, 其本构模型如(1)式所示:
| $ \sigma {\rm{ = }}\left( {1- D} \right)\left[{{f_{\rm{e}}}\left( \varepsilon \right) + {E_1}\int_0^t {\dot \varepsilon \exp \left( {-\frac{{t-\tau }}{{{\theta _1}}}} \right){\rm{d}}\tau } + {E_2}\int_0^t {\dot \varepsilon \exp \left( {-\frac{{t - \tau }}{{{\theta _2}}}} \right){\rm{d}}\tau } } \right] $ | (1a) |
| $ {f_{\rm{e}}}\left( \varepsilon \right) = {\sigma _m}\left\{ {1- \exp \left[{-\sum\limits_{i = 1}^n {\frac{{{{\left( {m\varepsilon } \right)}^i}}}{i}} } \right]} \right\} $ | (1b) |
式中, σ为名义应力, MPa; ε为名义应变;
2014年, 刘志林等[87]基于高应变率条件下的简化ZWT本构模型((2)式), 描述了单轴压缩条件下底排药柱的变形, 并将该本构模型植入LS-DYNA软件中对高速冲击条件下底排药柱的变形进行了数值仿真, 通过与实验数据进行比较发现, 在应变小于3%范围内仿真值与实验值吻合较好。
| $ \sigma {\rm{ = }}\left( {{E_0} + {E_1}} \right)\varepsilon + \alpha {\varepsilon ^2} + \beta {\varepsilon ^{3 + }}{E_2}\int_0^t {\dot \varepsilon \exp \left( {-\frac{{t-\tau }}{{{\theta _2}}}} \right){\rm{d}}\tau } $ | (2) |
式中, E0、α和β为弹性系数, MPa; (2)式右侧前三项描述非线性弹性平衡响应。
2015年, 郑健等[88]将(2)式所示的简化ZWT本构模型植入ABAQUS软件, 成功进行了改性双基固体推进剂的动态断裂韧性仿真研究。
(2) 1988年, Burke等[89]提出了适合于固体推进剂类材料的粘-超弹性本构模型。近年来, 粘-超弹性本构模型逐渐成为描述高应变率加载条件下固体推进剂变形的新模型。2011年, Yildirim[90]采用Yeoh应变能函数描述老化对固体推进剂变形行为的影响, 最终构建了反映老化对变形特性影响的固体推进剂高应变率压缩变形粘-超弹性本构模型。2014年, 基于粘-超弹性本构模型的思想, 常新龙等[91]在考虑温度影响的基础上构建了可以描述不同温度高应变率压缩条件下HTPB固体推进剂变形的本构模型, 模型中采用Moonev-Rivlin应变能函数对Burke本构模型进行改进。
(3) 2002年, Ho[49]采用包含应变能函数的唯象型非线性粘弹性本构模型描述了高应变率单轴压缩条件下HTPB固体推进剂的变形, 模型中采用应变能函数描述推进剂变形时损伤的演化。虽然, Ho建立的本构模型时间较早, 但是, 由于需要分段构建应变能函数, 且所建模型不能很好地描述低温以及较大应变率范围内固体推进剂的变形, 因而一直未能得到广泛应用。
4.2 当前研究中存在不足及展望为描述固体推进剂在不同加载条件下的变形, 近年来, 国内外研究者在本构模型的研究上取得了新的进展, 但已经开展的有关研究, 仍主要存在以下两方面的不足:
(1) 国内外研究者主要采用含损伤的积分型非线性粘弹性本构模型描述准静态加载条件下固体推进剂的变形, 但是, 已经建立的有关模型不能描述推进剂变形时应力-应变曲线多段特性(图 5b), 而且基于细观方法构建的本构模型, 其损伤函数的参数值不容易确定。
(2) 缺乏能够有效描述动态加载条件下固体推进剂大变形的非线性粘弹性本构模型, 尤其是针对温度和动态加载双重作用下的情况以及中应变率(1~102 s-1)加载下的情况。虽然, ZWT本构模型广泛用于描述高应变率压缩加载条件下固体推进剂的变形, 但以下几点不足严重限制了该模型的使用:首先, 其松弛时间量级决定了该模型不能对中应变率加载条件下材料的变形进行有效的描述; 其次, 含损伤的改进型ZWT本构模型相对原始ZWT本构模型能够描述更大应变范围内固体推进剂的变形, 但仍不能有效描述推进剂的整个变形过程; 第三, 该模型缺乏反映温度效应的表达式; 第四, 损伤因子是改进型ZWT本构模型的关键性参数, 但该参数的值不容易确定和描述, 且要求其值在分段点处一阶二次连续。虽然, 粘-超弹性本构模型成为描述高应变率条件下固体推进剂变形的新模型, 但该模型本身不含力学损伤项, 因而不能很好地描述固体推进剂的大变形。其次, 在低温和动态加载的双重作用下, 固体推进剂变硬变脆, 因而继续使用粘-超弹性本构模型描述固体推进剂的变形是不太合适的。即使通过数据拟合在粘-超弹性本构模型中以联乘的形式考虑温度的影响, 也不能很好地描述低温动态加载条件下固体推进剂的变形。
如前文所述, 损伤是造成固体推进剂具有非线性粘弹性特性的内在原因, 因此, 采用含损伤的积分型非线性粘弹性本构模型描述推进剂在不同加载条件下的变形是最为合适的。同时, 由于固体推进剂在准静态和动态加载条件下具有不同的损伤形式, 而基于宏观方法构建损伤函数不涉及推进剂变形时的细观损伤形式, 因此, 作者认为基于宏观方法的含损伤的积分型非线性粘弹性本构模型在描述准静态和动态加载条件下固体推进剂的变形时具有很大的优势, 可以成为今后研究的重点, 但损伤函数的推导和求解是难点, 需要研究者根据不同加载条件下固体推进剂的变形进行合理的分析。2015年, 在描述动态单轴拉伸条件下HTPB固体推进剂的变形时, 王哲君等[29]已经进行了有效的尝试, 其通过宏观方法构建了单一内变量的损伤函数, 最终获得了含损伤的积分型非线性粘弹性本构模型, 将预测应力值与实验数据进行比较发现, 除了非常大的应变处以外, 预测值与实验值均吻合较好。
5 结论从固体推进剂的力学性能实验测试方法、力学性能参数的确定以及本构模型的构建三个方面, 对固体推进剂力学性能和本构模型的研究进展以及当前研究中存在的不足等进行了较为详细的论述和分析, 认为今后需要重点研究的内容可以概括为:
(1) 实验研究。近年来, 国内外研究者主要在固体推进剂的准静态多轴拉压力学性能实验、动态单轴拉伸力学性能实验以及动态单轴断裂力学性能实验的研究上取得了新的进展。但是, 动态加载条件下和多轴应力状态下固体推进剂力学性能的实验测试方法研究仍存在相当大的难度, 为此, 可以借鉴以下三个方面的内容开展进一步的研究:第一, 借鉴基于SHTB技术的高应变率单轴拉伸力学性能实验测试方法, 但要特别注意实验过程中应变率的稳定性以及实验件的安装方法等问题; 第二, 借鉴中应变率条件下力学性能实验研究的新测试方法; 第三, 借鉴基于单轴试验机开展多轴力学性能实验研究的测试方法, 将这些测试方法与高应变率实验装置有效结合, 可以成为今后开展动态加载条件下固体推进剂多轴力学性能实验研究的新方法。
(2) 力学性能参数的确定。近年来, 国内外研究者发现了特定加载条件下固体推进剂变形时应力-应变曲线的多段特性, 并采用不同理论对这些曲线特性进行了讨论; 同时, 针对固体推进剂典型力学性能参数的确定给出了新的分析方法。但已经开展的有关研究不能有效适用于固体推进剂的复杂应力-应变曲线特性分析和力学性能参数的确定, 同时, 缺乏针对动态加载条件下固体推进剂损伤形式的深入研究, 缺乏针对不同应力状态下力学性能参数相互之间关系的讨论和分析。为此, 可以在以下三个方面开展进一步的研究:第一, 借鉴其它非金属材料曲线特性分析和力学性能参数确定的研究方法; 第二, 基于高速摄像技术以及散斑分析方法, 研究动态加载条件下固体推进剂的损伤形式; 第三, 在新的有效的多轴力学性能实验研究的基础上, 获得不同应力状态下较为完备的固体推进剂力学性能参数值。
(3) 本构模型构建。含损伤的积分型非线性粘弹性本构模型广泛用于描述准静态加载条件下固体推进剂的变形, 但不能描述应力-应变曲线多段特性, 而且基于细观方法构建的本构模型, 其损伤函数的参数值不容易确定。ZWT本构模型广泛用于描述高应变率压缩加载条件下固体推进剂的变形, 粘-超弹性本构模型是描述高应变率条件下固体推进剂变形的新模型, 但这些模型均不能十分有效地描述动态加载条件下固体推进剂的大变形非线性粘弹性特性。由于基于宏观方法构建含损伤的积分型非线性粘弹性本构模型不涉及固体推进剂变形时的细观损伤形式, 因此, 该类本构模型在描述准静态和动态加载条件下固体推进剂的变形时具有很大的优势, 可以成为今后研究的重点, 但损伤函数的推导和求解是难点, 需要研究者根据不同加载条件下固体推进剂的变形进行合理分析。
| [1] |
李葆萱, 王克秀.
固体推进剂性能[M]. 西安: 西北工业大学出版社, 1990: 46.
|
| [2] |
Zalewski R, Wolszakiewicz T. Analysis of uniaxial tensile tests for homogeneous solid propellants under various loading conditions[J].
Central European Journal of Energetic Materials, 2011, 8(4): 223-231. |
| [3] |
Method for determining the tensile properties of solid rocket propellants[M]. CPIA Publish, 1957.
|
| [4] |
GJB 770B-2005. 火药试验方法[S]. 国防科学技术工业委员会.
|
| [5] |
QJ 2328A-2005. 复合固体推进剂高温加速老化试验方法[S]. 国防科学技术工业委员会.
|
| [6] |
Blumenthal W R, Thompson D G, Cady C M, et al. Compressive properties of PBXN-110 and its HTPB-based binder as a function of temperature and strain rate[C]//Proceedings of the 12th International Detonation Symposium. Washington, DC: Office of Naval Research, 2002: 530-549.
|
| [7] |
Iwamoto T, Yokoyama T. Effects of radial inertia and end friction in specimen geometry in split Hopkinson pressure bar test: a computational study[J].
Mechanics of Materials, 2012, 51: 97-109. DOI:10.1016/j.mechmat.2012.04.007 |
| [8] |
Bills K W, Wiegan J H. Relation of mechanical properties to solid rocket motor failure[J].
AIAA Journal, 1963, 9(1): 2116-2123. |
| [9] |
王至存. 定速拉伸的固体推进剂双轴板条的应力分析[J].
固体火箭技术, 1995, 18(1): 54-59. WANG Zhi-cun. Stress analysis of the solid propellant biaxial strip under constant-rate tensile test[J]. Journal of Solid Rocket Technology, 1995, 18(1): 54-59. |
| [10] |
张丽华, 蔡建. 固体推进剂双轴拉伸试验的初步研究[J].
兵工学报, 1995, 16(1): 20-22. ZHANG Li-hua, CAI Jian. Preliminary study of the biaxial tensile test on solid propellant[J]. Acta Armamentarii, 1995, 16(1): 20-22. |
| [11] |
强洪夫, 王广, 张炜, 等. 固体发动机推进剂/粘结界面失效机理、模拟表征和优化设计[R]. 973-61338, 2005-2010.
|
| [12] |
贾永刚, 张为华, 张炜. 固体推进剂双向拉伸试件优化设计及试验[J].
推进技术, 2011, 32(5): 737-740. JIA Yong-gang, ZHANG Wei-hua, ZHANG Wei. Optimal design and examination study of biaxial tensile specimens for solid propellant[J]. Journal of Propulsion Technology, 2011, 32(5): 737-740. |
| [13] |
Jalocha D, Constantinescu A, Nevière R. Prestrained biaxial DMA investigation of viscoelastic nonlinearities in highly filled elastomers[J].
Polymer Testing, 2015, 42: 37-44. DOI:10.1016/j.polymertesting.2015.01.005 |
| [14] |
Lindsey G H, Schapery R A, Williams M L, et al. The triaxial tension failure of viscoelastic materials[R]. AD0419128, 1963.
|
| [15] |
Jones J W, Knauss W G. Propellant failure criteria[R]. 1965: 65-157.
|
| [16] |
Sanal Kumar V R. Thermoviscoelastic characterization of a composite solid propellant using tubular test[J].
Journal of Propulsion and Power, 2003, 19(3): 397-404. DOI:10.2514/2.6143 |
| [17] |
Liu C T, Wickham D, Smith G. Effects of confining pressure on the crack growth behavior in a filled elastomer subjected to a constant strain rate[R]. ADA423471, 2004.
|
| [18] |
张亚. HTPB复合固体推进剂破坏准则的试验和理论研究[D]. 西安: 第二炮兵工程大学, 2010.
ZHANG Ya. Research on failure mechanism and failure criterion of HTPB composite solid propellant[D]. Xi'an: Xi'an Hi-Tech Institute, 2010. |
| [19] |
Zhang J, Ju Y, Zhou C. Experimental research on cohesion and internal friction angle of the double-base propellant[J].
Propellants, Explosives, Pyrotechnics, 2013, 38(3): 351-357. DOI:10.1002/prep.201200121 |
| [20] |
Liu C T. Evaluation of damage fields near crack tips in a composite solid propellant[J].
Journal of Spacecraft Rockets, 1991, 28(1): 64-70. DOI:10.2514/3.26210 |
| [21] |
Liu C T, Smith W G. Near-tip behavior in a particulate material under constant strain rate including temperate and thickness effects[R]. ADA410504, 2001.
|
| [22] |
Liu C T. Monitoring Microstructural Evolution, Crack formation, and damage characteristics near crack tip in a highly filled elastomer-using digital radiography X-ray techniques[J].
Experimental Mechanics, 2007, 47: 79-85. DOI:10.1007/s11340-006-9141-2 |
| [23] |
张亚, 强洪夫, 杨月诚. 国产HTPB复合固体推进剂Ⅰ-Ⅱ型裂纹断裂性能实验研究[J].
含能材料, 2007, 15(4): 359-362. ZHANG Ya, QIANG Hong-fu, YANG Yue-cheng. Fracture behavior of HTPB composite propellant in Ⅰ-Ⅱ mixed mode crack[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2007, 15(4): 359-362. |
| [24] |
龙兵, 常新龙, 刘万雷, 等. HTPB推进剂低温断裂性能试验研究[J].
推进技术, 2014, 35(9): 1278-1282. LONG Bing, CHANG Xin-long, LIU Wan-lei, et al. Experimental study on low temperature fracture properties of HTPB propellant[J]. Journal of Propulsion Technology, 2014, 35(9): 1278-1282. |
| [25] |
Sun C, Xu J, Chen X, Zheng J, et al. Strain rate and temperature dependence of the compressive behavior of a composite modified double-base propellant[J].
Mechanics of Materials, 2015, 89: 35-46. DOI:10.1016/j.mechmat.2015.06.002 |
| [26] |
Balzer J E, Siviour C R, Walley S M, et al. Behaviour of ammonium perchlorate-based propellants and a polymer-bonded explosive under impact loading[J].
Proceeding of the Royal Society of London, 2004, 460(2043): 781-806. DOI:10.1098/rspa.2003.1188 |
| [27] |
强洪夫, 王广, 武文明, 等. 一种用于非金属材料力学试验的单轴高速拉伸试验夹具: 中国专利: ZL 2013 2 0012760. 5[P], 2013-07-13.
|
| [28] |
王哲君, 强洪夫, 王广, 等. 低温高应变率条件下HTPB推进剂拉伸力学性能研究[J].
推进技术, 2015, 36(9): 1426-1432. WANG Zhe-jun, QIANG Hong-fu, WANG Guang, et al. Tensile Mechanical Properties of HTPB Propellant at Low Temperature and High Strain Rate[J]. Journal of Propulsion Technology, 2015, 36(9): 1426-1432. |
| [29] |
Wang Z, Qiang H, Wang G, et al. Tensile mechanical properties and constitutive model for HTPB propellant at low temperature and high strain rate[J].
Journal of Applied Polymer Science, 2015, 132(24) DOI:10.1002/APP.42104 |
| [30] |
Murri W G, Gupta Y M, Curran D R. Fracture and fragmentation of high energy propellant[R]. UCRL-15160, 1979.
|
| [31] |
黄风雷, 王泽平, 丁  . 复合固体推进剂动态断裂研究[J].
兵工学报, 1995, 16(2): 47-50.
. 复合固体推进剂动态断裂研究[J].
兵工学报, 1995, 16(2): 47-50. HUANG Feng-lei, WANG Ze-ping, DING Jing. Dynamic fracture of composite solid propellant[J]. Acta Armamentarii, 1995, 16(2): 47-50. |
| [32] |
龙兵, 常新龙, 张有宏, 等. 高应变率下HTPB推进剂动态断裂性能研究[J].
推进技术, 2015, 36(3): 471-475. LONG Bing, CHANG Xin-long, ZHANG You-hong, et al. Study on dynamic fracture properties of HTPB propellant under high strain rate[J]. Journal of Propulsion Technology, 2015, 36(3): 471-475. |
| [33] |
Long B, Chang X, Hu K, et al. Effects of temperature and strain rate on the dynamic fracture properties of HTPB propellant[J].
Propellants, Explosives, Pyrotechnics, 2015, 40(4): 479-483. DOI:10.1002/prep.v40.4 |
| [34] |
Harding J, Wood E D, Campbell J D. Tensile testing of material at impact rates of strain[J].
Journal of Mechanical Engineering Science, 1960, 2(1): 88-96. |
| [35] |
Ogawa K. Impact-tension compression test by using a split-hopkinson bar[J].
Experimental Mechanics, 1984, 24(2): 81-86. DOI:10.1007/BF02324987 |
| [36] |
Staab G H, Gliat A. A direct-tension split hopkinson bar for high strain-rate testing[J].
Experimental Mechanics, 1991, 31(2): 232-235. |
| [37] |
陈荣. 一种PBX炸药试验在复杂应力动态加载下的力学性能实验研究[D]. 长沙: 国防科学技术大学, 2010.
CHEN Rong. Experimental studies on mechanical properties of a PBX under various dynamic loading conditions[D]. Changsha: National University of Defense Technology, 2010. |
| [38] |
Owens A T, Tippur H V. A tensile split hopkinson bar for testing particulate polymer composites under elevated rates of loading[J].
Experimental Mechanics, 2009, 49(6): 799-811. DOI:10.1007/s11340-008-9192-7 |
| [39] |
Othman R, Guegan P, Challita G, et al. A modified servo-hydraulic machine for testing at intermediate strain rates[J].
International Journal of Impact Engineering, 2009, 36(3): 460-467. DOI:10.1016/j.ijimpeng.2008.06.003 |
| [40] |
Song B, Syn C J, Grupido C L, et al. A long split hopkinson pressure bar (LSHPB) for intermediate-rate characterization of soft materials[J].
Experimental Mechanics, 2008, 48(6): 809-815. DOI:10.1007/s11340-007-9095-z |
| [41] |
Brieu M, Diani J, Bhatnagar N. A new biaxial tension test fixture for uniaxial testing machine-a validation for hyperelastic behavior of rubber-like materials[J].
Journal of Testing and Evaluation, 2007, 35(4): 364-372. |
| [42] |
Kossa A. A new biaxial compression fixture for polymeric foams[J].
Polymer Testing, 2015, 45: 47-51. DOI:10.1016/j.polymertesting.2014.08.003 |
| [43] |
唐维, 颜熹琳, 李明, 等. 基于间接三轴拉伸破坏试验的某TATB基PBX强度准则适应性分析[J].
含能材料, 2015, 23(6): 532-536. TANG Wei, YAN Xi-lin, LI Ming, et al. Adaptability analysis of strength criterion on TATB based PBX by indirect triaxial tensile collapse test[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2015, 23(6): 532-536. DOI:10.11943/j.issn.1006-9941.2015.06.005 |
| [44] |
Bailly P, Delvare F, Vial J, et al. Dynamic behavior of an aggregate material at simultaneous high pressure and strain rate: SHPB triaxial tests[J].
International Journal of Impact Engineering, 2011, 38(2-3): 73-84. DOI:10.1016/j.ijimpeng.2010.10.005 |
| [45] |
Francis E C, Carlton C H. Some aspects of nonlinear mechanical behavior of a composite propellant[J].
Journal of Spacecraft Rockets, 1969, 6(1): 65-69. DOI:10.2514/3.29532 |
| [46] |
赖建伟, 常新龙, 龙兵, 等. 低温和应变率对HTPB推进剂压缩力学性能影响[J].
固体火箭技术, 2012, 35(6): 792-798. LAI Jian-wei, CHANG Xin-long, LONG Bing, et al. Effects of low temperature and strain rate on compressive mechanical properties of HTPB propellant[J]. Journal of Solid Rocket Technology, 2012, 35(6): 792-798. |
| [47] |
Landsem E, Jensen T L, Hansen F K, et al. Mechanical properties of smokeless composite rocket propellants based on prilled ammonium dinitramide[J].
Propellants, Explosives, Pyrotechnics, 2012, 37(6): 691-698. DOI:10.1002/prep.201200004 |
| [48] |
胡少青, 鞠玉涛, 孟红磊, 等. 双基推进剂压缩力学性能的应变率相关性研究[J].
弹道学报, 2011, 23(4): 75-79. HU Shao-qing, JU Yu-tao, MENG Hong-lei, et al. Effects of strain rate on mechanical properties of DBP under uniaxial compression condition[J]. Journal of Ballistics, 2011, 23(4): 75-79. |
| [49] |
Ho S Y. High strain-rate constitutive models for solid rocket propellants[J].
Journal of Propulsion and Power, 2002, 18(5): 1106-1111. DOI:10.2514/2.6041 |
| [50] |
赖建伟. 固体推进剂药柱低温力学性能与结构完整性研究[D]. 西安: 第二炮兵工程大学, 2013.
LAI Jian-wei. Research on mechanical properties and structural integrity of solid propellant grain at low temperature[D]. Xi'an: Xi'an Hi-Tech Institute, 2013. |
| [51] |
Liu C T. Effect of load history on the cumulative damage in a composite solid propellant[R]. AIAA 86-1015, 1986.
|
| [52] |
Chu H, Chou J. Effect of cooling load on the safety factor of propellant grains[J].
Journal of Propulsion and Power, 2013, 29(1): 27-33. DOI:10.2514/1.B34579 |
| [53] |
Landsem E, Jensen T L, Hansen F K. Neutral polymeric bonding agents (NPBA) and their use in smokeless composite rocket propellants based on HMXGAP-BuNENA[J].
Propellants, Explosives, Pyrotechnics, 2012, 37(5): 581-591. DOI:10.1002/prep.v37.5 |
| [54] |
Shekhar H. Effect of temperature on mechanical properties of solid rocket propellants[J].
Defence Science Journal, 2011, 61(6): 529-533. |
| [55] |
侯林法.
复合固体推进剂[M]. 北京: 宇航出版社, 1994: 276-278.
|
| [56] |
杨凤林, 庞爱民, 张小平. 复合固体推进剂单向拉伸曲线分析[J].
固体火箭技术, 2001, 24(3): 54-57. YANG Feng-lin, PANG Ai-min, ZHANG Xiao-ping. An analysis on the stress-strain curves of composite solid propellant[J]. Journal of Solid Rocket Technology, 2001, 24(3): 54-57. |
| [57] |
Renganathan K, Nageswara Rao B, Jana M K. Failure assessment on a strip biaxial tension specimen for a HTPB-based propellant material[J].
Propellants, Explosives, Pyrotechnics, 1999, 24(6): 349-352. DOI:10.1002/(ISSN)1521-4087 |
| [58] |
Shekhar H. Studies on stress-strain curves of aged composite solid rocket propellants[J].
Defence Science Journal, 2012, 62(2): 90-94. DOI:10.14429/dsj |
| [59] |
Neviére R. An extension of the time-temperature superposition principle to non-linear viscoelastic solids[J].
International Journal of Solids and Structures, 2006, 43(17): 5295-5306. DOI:10.1016/j.ijsolstr.2005.09.009 |
| [60] |
李敬明, 郑雪, 李伟, 等. NEPE推进剂拉伸破坏过程实验研究[J].
含能材料, 2009, 17(2): 241-250. LI Jing-ming, ZHENG Xue, LI Wei, et al. Experimental study on tensile damage process of NEPE propellant[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2009, 17(2): 241-250. |
| [61] |
Darwell H M, Parker A, Leemin H. Mechanical behavior of cast-double-base propellants in rocket motors[J].
Journal of Spacecraft and Rocket, 1966, 3(3): 399-407. DOI:10.2514/3.28459 |
| [62] |
Liu C, Thompson D G. Mechanical response and failure of high performance propellant (HPP) subject to uniaxial tension[J].
Mechanics of Time-Dependent Materials, 2015, 19(2): 95-115. DOI:10.1007/s11043-015-9254-z |
| [63] |
张建彬, 鞠玉涛, 周长省. 双基固体推进剂的特性研究[J].
固体火箭技术, 2013, 36(1): 94-97. ZHANG Jian-bin, JU Yu-tao, ZHOU Chang-sheng. Study on the characteristics of the double-base solid propellant[J]. Journal of Solid Rocket Technology, 2013, 36(1): 94-97. |
| [64] |
Lieb R J, Leadore M G. Mechanical response comparison of gun propellants evaluated under equivalent time-temperature conditions[R]. AD-A270 479, 1993.
|
| [65] |
张晓军, 常新龙, 赖建伟, 等. HTPB推进剂低温拉伸/压缩力学性能对比[J].
固体火箭技术, 2013, 36(6): 771-774. ZHANG Xiao-jun, CHANG Xin-long, LAI Jian-wei, et al. Comparative research of tensile and compressive mechanical properties of HTPB propellant at low temperature[J]. Journal of Solid Rocket Technology, 2013, 36(6): 771-774. |
| [66] |
Gazonas G A, Ford J C. Uniaxial compression testing of M30 and JA2 gun propellants using a statistical design strategy[J].
Experimental Mechanics, 1992, 32(2): 154-162. DOI:10.1007/BF02324727 |
| [67] |
Naik N K, Shankar P J, Kavala V R, at al. High strain rate mechanical behavior of epoxy under compressive loading: Experimental and modeling studies[J].
Materials Science and Engineering A, 2011, 528(3): 846-854. DOI:10.1016/j.msea.2010.10.099 |
| [68] |
Ouelleta S, Croninb D, Worswick M. Compressive response of polymeric foams under quasi-static, medium and high strain rate conditions[J].
Polymer Testing, 2006, 25(6): 731-743. DOI:10.1016/j.polymertesting.2006.05.005 |
| [69] |
强洪夫. 固体火箭发动机药柱结构完整性数值仿真与实验研究[D]. 西安: 西安交通大学, 1998.
QIANG Hong-fu. Numerical analysis and experimental researches on solid rocket motor grain structure integrity[D]. Xi'an: Xi'an Jiaotong University, 1998. |
| [70] |
张中水, 许进升, 陈雄. 基于EPDM绝热层拉压不同性的研究[J].
化工新型材料, 2015, 43(3): 170-172. ZHANG Zhong-shui, XU Jin-sheng, CHEN Xiong. Research for EPDM insulation based on different properties of tension and compression[J]. New Chemical Materials, 2015, 43(3): 170-172. |
| [71] |
Deng K, Yang J, Huang W, et al. A new method to obtain shear modulus of solid propellant[J].
Acta Astronautica, 2011, 69(7-8): 440-444. DOI:10.1016/j.actaastro.2011.05.030 |
| [72] |
Knauss W G, Zhu W. Nonlinearly viscoelastic behavior of polycarbonate I.Response under pure shear[J].
Mechanics of Time Dependent Materials, 2002, 6(3): 231-269. DOI:10.1023/A:1016203131358 |
| [73] |
Ren P, Hou X, He G R, et al. Comparative research of tensile and compressive modulus of composite solid propellant for solid rocket motor[J].
Journal of Astronautics, 2010, 31(10): 2354-2359. |
| [74] |
阳建红, 俞茂宏, 侯根良, 等. HTPB复合固体推进剂含损伤和老化本构研究[J].
推进技术, 2002, 23(6): 509-512. YANG Jian-hong, YU Mao-hong, HOU Gen-liang, et al. Research on the constitutive equations of HTPB composite solid propellant with damage and aging[J]. Journal of Propulsion Technology, 2002, 23(6): 509-512. |
| [75] |
彭威, 郑坚, 白鸿柏, 等. 复合推进剂微裂纹损伤本构模型研究[J].
固体火箭技术, 2003, 26(1): 33-37. PENG Wei, ZHENG Jian, BAI Hong-bai, et al. Study on micro-cracking damage constitutive model of HTPB composite solid propellant[J]. Journal of Solid Rocket Technology, 2003, 26(1): 33-37. |
| [76] |
Xu F, Sofronis P, Aravas N. Constitutive modeling of solid propellant materials with evolving microstructural damage[J].
Journal of the Mechanics and Physics of Solids, 2008, 56(5): 2050-2073. DOI:10.1016/j.jmps.2007.10.013 |
| [77] |
Park S W, Schapery R A. A viscoelastic constitutive model for particulate composites with growing damage[J].
International Journal of Solids and Structures, 1997, 34(8): 931-947. DOI:10.1016/S0020-7683(96)00066-2 |
| [78] |
孟红磊, 鞠玉涛. 含损伤非线性粘弹性本构模型及数值仿真应用[J].
固体火箭技术, 2012, 35(6): 764-768, 772. MENG Hong-lei, JU Yu-tao. Nonlinear viscoelastic equation with cumulative damage and its application on numerical simulation[J]. Journal of Solid Rocket Technology, 2012, 35(6): 764-768, 772. |
| [79] |
Xu J, Chen X, Wang H, et al. Thermo-damage-viscoelastic constitutive model of HTPB composite propellant[J].
International Journal of Solids and Structures, 2014, 51(18): 3209-3217. DOI:10.1016/j.ijsolstr.2014.05.024 |
| [80] |
姚东, 张光善, 高波. 考虑应力状态的HTPB/AP推进剂含损伤热-粘弹性本构方程[J].
固体火箭技术, 2014, 37(4): 496-499, 509. YAO Dong, ZHANG Guang-shan, GAO Bo. Constitutive equations involving damage for HTPB/AP propellant considering stress state[J]. Journal of Solid Rocket Technology, 2014, 37(4): 496-499, 509. |
| [81] |
Matheson E R, Nguyen D Q. A rate-dependent viscoelastic damage model for simulation of solid propellant impacts[J].
AIP Conference Proceedings, 2006, 845(1): 913-916. |
| [82] |
Shekhar H, Kankane D K. Viscoelastic characterization of different solid rocket propellants using the maxwell spring-dashpot model[J].
Central European Journal of Energetic Materials, 2012, 9(3): 189-199. |
| [83] |
王礼立, 施绍裘, 陈江瑛, 等. Z-W-T非线性粘弹性本构关系的研究与应用[J].
宁波大学学报, 2000, 13(增刊): 141-149. WANG Li-li, SHI Shao-qiu, CHEN Jiang-ying, et al. Z-W-T nonlinear viscoelastic constitutive research and application[J]. Journal of Ningbo University, 2000, 13(Suppl.): 141-149. |
| [84] |
王蓬勃, 王政时, 鞠玉涛, 等. 双基推进剂高应变率型本构模型的实验研究[J].
固体火箭技术, 2012, 35(1): 69-72. WANG Peng-bo, WANG Zheng-shi, JU Yu-tao, et al. Experimental research on rate dependent constitutive relation of double-base propellant under impact load[J]. Journal of Solid Rocket Technology, 2012, 35(1): 69-72. |
| [85] |
孙朝翔, 鞠玉涛, 郑亚, 等. 双基推进剂的高应变率力学特性及其含损伤ZWT本构[J].
爆炸与冲击, 2013, 33(5): 507-512. SUN Chao-xiang, JU Yu-tao, ZHENG Ya, et al. Mechanical properties of double-base propellant at high strain rates and its damage-modified ZWT constitutive model[J]. Explosion and Shock Waves, 2013, 33(5): 507-512. DOI:10.11883/1001-1455(2013)05-0507-06 |
| [86] |
王礼立, 董新龙, 孙紫建. 高应变率下计及损伤演化的材料动态本构行为[J].
爆炸与冲击, 2006, 26(3): 193-198. WANG Li-li, DONG Xin-long, SUN Zi-jian. Dynamic constitutive behavior of materials at high strain rate taking account of damage evolution[J]. Explosion and Shock Waves, 2006, 26(3): 193-198. DOI:10.11883/1001-1455(2006)03-0193-06 |
| [87] |
刘志林, 王晓鸣, 姚文进, 等. 底排药的高应变率动态响应实验和仿真[J].
含能材料, 2014, 22(4): 529-534. LIU Zhi-lin, WANG Xiao-ming, YAO Wen-jin, et al. Numerical simulation and mechanical behavior of base bleed grain at high strain rate[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2014, 22(4): 529-534. |
| [88] |
郑健, 汪文强, 陈雄, 等. 基于微观结构分析的CMDB推进剂动态断裂韧性加载率敏感性研究[J].
推进技术, 2015, 36(6): 940-946. ZHENG Jian, WANG Wen-qiang, CHEN Xiong, et al. Effects of loading rate and microstructure on dynamic fracture toughness of CMDB propellant[J]. Journal of Propulsion Technology, 2015, 36(6): 940-946. |
| [89] |
Burke M A, Woytowitz P J, Derbalian G K, et al. A nonlinear viscoelastic constitutive model for solid propellant[R]. BMO-TR-88-61, 1988.
|
| [90] |
Yildirim H C, Özupek Ş. Structural assessment of a solid propel¬lant rocket motor: Effects of aging and damage [J]. Structural assessment of a solid propellant rocket motor: Effects of aging and damage[J]. Aerospace Science and Technology, 2011, 15(8): 635-641.
|
| [91] |
常新龙, 赖建伟, 张晓军, 等. HTPB推进剂高应变率粘弹性本构模型研究[J].
推进技术, 2014, 35(1): 123-127. CHANG Xin-long, LAI Jian-wei, ZHANG Xiao-jun, et al. High strain-rate viscoelastic constitutive model for HTPB propellant[J]. Journal of Propulsion Technology, 2014, 35(1): 123-127. |
Mechanical properties and constitutive models of solid propellants were reviewed from experimental techniques, mechanical parameters determination and developing constitutive models. Based on that, the current shortages and future research contents were also proposed.




