2. 北京理工大学爆炸科学与技术国家重点实验室,北京 100081
2. State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing 100081,China
水夹层间隔靶可代替舰艇、潜艇结构,模拟水下聚能装药对舰艇、潜艇的破坏效果。采用水夹层间隔靶等效代替均质靶板,应用于破甲弹威力验收靶场试验可大大降低试验费用,避免浪费。因此,射流对水夹层间隔靶的侵彻备受关注,建立其侵彻理论模型意义重大。
现有文献多见于聚能射流对水[1-3]以及间隔靶板[4-8]的侵彻,而对射流侵彻含水夹层间隔靶的研究相对较少。裴明敬[9]对聚能杆式弹丸侵彻水夹层复合靶进行了试验,研究了炸高对聚能装药侵彻水夹层复合靶效果的影响。张莉[10]在聚能装药爆炸成型弹丸侵彻多层含水复合装甲实验中,利用脉冲X光高速摄影技术和电探针测试技术获得了弹丸的飞行特性和对含水复合装甲的侵彻规律。D.R. Saroha[11-12]将多通道闪光摄像仪应用于射流侵彻含水夹层靶板实验中,研究了侵彻过程中射流的衰减、侵彻方向以及在水中形成的空腔。并用数值模拟方法对射流侵彻过程中的断裂情况进行了仿真,与实验结果吻合较好。Max Peters[13]以射流侵彻水夹层间隔靶实验为依据,通过AUTODYN附加开发程序,较好地对射流侵彻过程进行了仿真。Shi-long Xing[14]将锥形-圆形药型罩应用于聚能装药战斗部,通过数值模拟获得了射流的形成及其对含水夹层间隔靶的破坏效果。以上对聚能装药侵彻水夹层间隔靶的研究多以数值模拟和实验方法为主,而在理论研究方面尚未见相关公开文献。
本研究结合准定常侵彻理论和数学归纳法建立了射流侵彻水夹层间隔靶理论模型。设计了射流侵彻水夹层间隔靶实验对理论模型进行验证,通过侵彻模型探讨了水夹层间隔靶结构变化对射流侵彻的影响。
2 侵彻模型的建立为了突出重点、简化工程计算,对射流侵彻水夹层间隔靶计算模型做如下假设:
(1) 连续射流在穿过水夹层间隔靶时未发生断裂和干扰;
(2) 在有效射流段,射流速度由头部至尾部随其长度呈线性减少;
(3) 射流和靶板均为不可压缩理想流体;
(4) 不考虑靶板强度的影响;
(5) 不考虑水的可压缩性和水中冲击波的影响;
(6) 射流在穿透靶板时不考虑靶背表面效应。
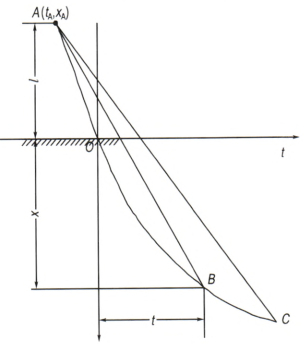
2.1 准定常侵彻理论[8]射流侵彻靶板准定常理论计算示意图如图 1所示,以射流着靶点为纵向坐标x的原点,以着靶时间为时间坐标t的原点。由虚拟原点理论可知,射流是从A点发出的一簇直线,每一直线的斜率对应射流微元的速度,l为虚拟源点到靶板的距离。曲线OBC为聚能射流侵彻深度随时间的变化曲线,曲线上任意点B的侵彻深度为x,该点的切线斜率为侵彻速度u,相应射流微元的速度vj为AB的斜率,射流侵彻终止点为C。如果射流速度恒定,则侵彻速度不变,AB将是直线,由于射流速度愈来愈慢,则AB为曲线。
|
图 1 射流准定常侵彻理论计算示意图 Fig.1 Calculation schematic of quasi-steady penetration theory of jet |
假设射流着靶时,长度为L,头部速度为vhead,尾部速度为vtail,则根据虚拟源点原理,可得图 1中虚拟源点A的坐标为:
| $ \left\{ \begin{align} &{{t}_{A}}=\frac{~\mathit{l}}{{{v}_{\rm{head}}}}=-\frac{L}{{{v}_{\rm{head}}}-{{v}_{\rm{tail}}}} \\ &{{x}_{\rm{A}}}=-l=\frac{{{v}_{\rm{head}}}L}{{{v}_{\rm{head}}}-{{v}_{\rm{tail}}}} \\ \end{align} \right. $ | (1) |
根据准定常侵彻理论可得射流微元速度vj与侵彻深度x的对应关系为:
| $ x =- {x_{\rm{A}}}\left[{{{\left( {\frac{{{v_{{\rm{head}}}}}}{{{v_{\rm{j}}}}}} \right)}^{\sqrt {{\rho _{\rm{j}}}/{\rho _{\rm{t}}}} }}-1} \right] = l\left[{{{\left( {\frac{{{v_{{\rm{head}}}}}}{{{v_{\rm{j}}}}}} \right)}^{^{\sqrt {{\rho _{\rm{j}}}/{\rho _{\rm{t}}}} }}}-1} \right] $ | (2) |
式中,ρj为射流密度,kg·m-3,ρt为靶板密度,kg·m-3。
2.2 射流侵彻水夹层间隔靶模型聚能射流侵彻水夹层间隔靶几何关系示意图如图 2所示。射流虚拟源点为A,水夹层间隔靶第n层靶板的厚度为sn,第n层水间隔的厚度为wn。射流开始侵彻第n层靶板时头部速度为vsn1,侵彻第n层靶板完成时头部速度为vsn2。射流侵彻第n层水间隔开始和完成时,头部速度为vwn1和vwn2。

|
图 2 射流侵彻水夹层间隔靶几何关系示意图 Fig.2 The geometric relationship sketch of spaced target with water layer penetrated by jet |
(1) 射流侵彻第一层靶板完成时
应用射流准定常侵彻理论可得,靶板1侵彻完成时聚能射流的头部速度vs12满足以下关系式:
| $ v_{s1}^2 = v_{s1}^1{\left( {1 + \frac{{{s_1}}}{{{l_1}}}} \right)^{-\sqrt {{\rho _{\rm{t}}}/{\rho _{\rm{j}}}} }} = {v_{{\rm{head}}}}{\left( {1 + \frac{{{s_1}}}{{{l_1}}}} \right)^{-\sqrt {{\rho _{\rm{t}}}/{\rho _{\rm{j}}}} }} $ | (3) |
(2) 射流侵彻第一层水完成时
再次应用准定常理论,可得第一层水侵彻完成时射流的相关参数为:
| $ \begin{array}{l} \left\{ \begin{array}{l} v_{w1}^2 = v_{w1}^1\left( {1 + \frac{{{w_1}}}{{{l_2}}}} \right)-\sqrt {{\rho _{\rm{w}}}/{\rho _{\rm{j}}}} \\ {l_1} + {s_1} = {l_2}\\ v_{w1}^1 = v_{s1}^2 \end{array} \right.\\ v_{w1}^2 = {v_{{\rm{head}}}}{\left( {1 + \frac{{{s_1}}}{{{l_1}}}} \right)^{-\sqrt {{\rho _{\rm{t}}}/{\rho _{\rm{j}}}} }}{\left( {1 + \frac{{{w_1}}}{{{l_1} + {s_1}}}} \right)^{-\sqrt {{\rho _{\rm{w}}}/{\rho _{\rm{j}}}} }} \end{array} $ | (4) |
式中,ρw为水的密度,kg·m-3。
(3) 射流侵彻第二层靶板完成时
| $ \begin{array}{l} \left\{ \begin{array}{l} v_{s2}^2 = v_{s2}^1{\left( {1 + \frac{{{s_2}}}{{{l_3}}}} \right)^{-\sqrt {{\rho _{\rm{t}}}/{\rho _{\rm{j}}}} }}\\ {l_3} = {l_2} + {w_1} = {l_1} + {s_1} + {w_1}\\ v_{s2}^1 = v_{w1}^2 \end{array} \right.\\ v_{s2}^2 = {v_{{\rm{head}}}}{\left( {1 + \frac{{{s_1}}}{{{l_1}}}} \right)^{-\sqrt {{\rho _{\rm{t}}}/{\rho _{\rm{j}}}} }}{\left( {1 + \frac{{{w_1}}}{{{l_1} + {s_1}}}} \right)^{-\sqrt {{\rho _{\rm{w}}}/{\rho _{\rm{j}}}} }}{\left( {1 + \frac{{{s_2}}}{{{l_1} + {s_1} + {w_1}}}} \right)^{ - \sqrt {{\rho _{\rm{t}}}/{\rho _{\rm{j}}}} }} \end{array} $ | (5) |
(4) 射流侵彻第n层(n≥3)靶板完成时
在穿透第n层钢靶板时,射流共侵彻了n层钢靶板和n-1层水介质,侵彻完成时头部速度为:
| $ \begin{array}{l} v_{sn}^2 = {v_{{\rm{head}}}}{\left( {1 + \frac{{{s_1}}}{{{l_1}}}} \right)^{-\sqrt {{\rho _{\rm{t}}}/{\rho _{\rm{j}}}} }}{\left( {1 + \frac{{{w_1}}}{{{l_1} + {s_1}}}} \right)^{-\sqrt {{\rho _{\rm{w}}}/{\rho _{\rm{j}}}} }} \cdots \\ \;\;\;\;\;\;{\left( {1 + \frac{{{w_n}_{-1}}}{{{l_1} + {s_1} + {w_1} + \cdots + {s_{n - 2}} + {w_{n - 2}} + {s_{n - 1}}}}} \right)^{ - \sqrt {{\rho _{\rm{w}}}/{\rho _{\rm{j}}}} }}\\ \;\;\;\;\;{\left( {1 + \frac{{{s_n}}}{{{l_1} + {s_1} + {w_1} + \cdots + {s_{n - 1}} + {w_{n - 1}}}}} \right)^{ - \sqrt {{\rho _{\rm{t}}}/{\rho _{\rm{j}}}} }} \end{array} $ | (6) |
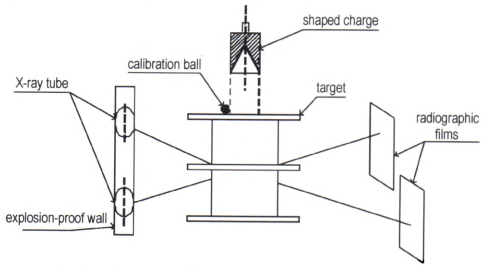
射流侵彻水夹层间隔靶实验总体布置如图 3所示。实验装药采用聚奥-8,装药直径为50 mm,装药高度为100 mm,炸高为90 mm,如图 4a所示。药型罩采用锥形药型罩,锥角为46°,壁厚为1 mm,材料为铜。水夹层间隔靶布置如图 4b所示,三层靶板之间用PVC管隔开,每层PVC管高度为100 mm,上层PVC管内介质为水,下层PVC管内介质为空气。每层靶板的厚度为4 mm,材料为A3钢,其上均铺有单面导电的靶板纸,用于测定射流穿透靶板的时间,进而求得射流在介质中侵彻的平均头部速度。
|
图 3 实验总体布置示意图 Fig.3 The overall arrangement diagram of the experiment |

|
图 4 实验装药及间隔靶布置图 Fig.4 The arrangement diagram of shaped charge and spaced target with water interlayer |
实验利用两台脉冲X光对射流侵彻水夹层间隔靶过程进行摄像,通过直径19.82 mm的钢珠进行标定,以获得侵彻过程中射流的形态及头部速度。
3.2 实验结果实验脉冲X光两次出光时间分别为31 μs和39.1 μs,拍摄得到X光片如图 5所示。由图 5可知,31~39.1 μs射流连续性较好,穿过第一层靶板后又在水中侵彻了一段距离,并在水中形成了侵彻空腔。

|
图 5 射流在水中侵彻的X光照片 Fig.5 X-ray photos of jet penetrating in water |
对实验X光照片进行测量得,两个时刻射流头部距第一层靶板的距离分别为p1=13.5 mm,p2=72.0 mm,标定钢球在X光照片上的直径长度为d=21mm。通过公式
另一发实验X光拍摄时间为48.9 μs和54.1 μs,拍摄得到射流侵彻状态如图 6所示。射流穿过水夹层间隔靶后,继续在空气中运行,射流在水中形成的空腔依然清晰可见。通过上述方法可以求得,在48.9~54.1 μs时间内射流平均头部速度为6163.5 m·s-1。由图 6b还可以看出,射流穿过第二层靶板在空气中继续运动一段距离后,出现了断裂情况。这是由于射流从钢靶进入空气时,被侵彻介质密度骤变,造成了射流的断裂和飞溅。

|
图 6 射流穿过水夹层间隔靶后在空气中运行的X光照片 Fig.6 The X-ray photos of jet penetrating in water |
由实验和理论模型得到的射流在各阶段的平均头部速度如表 1所示:
| 表 1 射流头部速度的实验值与理论值对比 Tab.1 Comparison of the average jet tip velocity of test and theory |
利用计时仪分别记录射流穿过靶板纸的时间,通过水间隔距离与时间的比值,即可得到射流在间隔水中的平均头部速度,其理论值与实验值最大误差为5.7%,平均误差为4.6%,如表 1所示。实验中测得射流接触靶板时刻头部速度约为8150 m·s-1,侵彻水夹层间隔靶完成时,实验射流头部速度衰减了24.4%,由理论得头部速度衰减了21.7%。理论结果与实验结果吻合较好,说明本文模型可以较好反应射流头部速度与水夹层间隔靶侵彻距离之间的关系。
由表 1中的对比结果还可看出,在各个侵彻阶段,射流头部速度理论值较实验值平均偏大约305 m·s-1。误差存在的原因主要是:射流侵彻水夹层间隔靶时,仅考虑了虚拟源点到靶板之间的距离变化,而重复开坑、射流飞溅及水的可压缩性对射流侵彻能力的影响并未列入考虑。可以通过在理论模型中附加修正项以减少误差,这是本研究下一步工作重点。
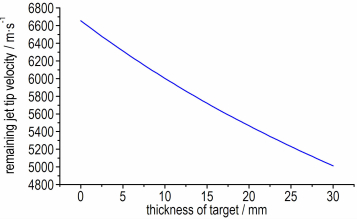
4 模型分析 4.1 靶板厚度的影响采用实验设计的水夹层间隔靶结构,两层靶板之间水间隔距离100 mm保持不变,通过变化靶板厚度,基于侵彻模型分析射流穿过水夹层间隔靶后剩余头部速度的变化规律。如图 7所示,随着间隔靶板厚度由0 mm增大到30 mm,射流剩余头部速度减少趋势变化不明显。间隔靶板厚度每增加5 mm,射流剩余头部速度约减少了260 m·s-1。
|
图 7 射流剩余头部速度随靶板厚度变化关系 Fig.7 The remaining jet tip velocity changing with target thickness |
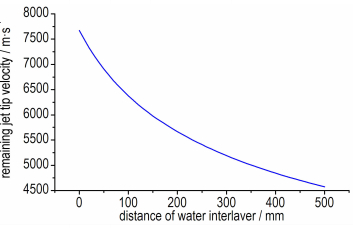
两层靶板厚度均为4 mm保持不变,以步长50 mm增加水间隔的距离,通过侵彻模型观察射流剩余头部速度随水间隔距离变化规律。如图 8所示,随着水间隔距离的增加,射流剩余头部速度基本上呈对数曲线减少。当水间隔的距离少于150 mm时,射流头部速度减少趋势较明显:间隔距离由0 mm增大到150 mm,射流剩余头部速度减少了1692 m·s-1,约降低了22.1%;而当水间隔距离由150 mm变为450 mm时,间隔距离增大了300 mm,头部速度仅减少了1278 m·s-1。因此,在靶板厚度一定时,选择合适的水间隔距离既可以兼顾水夹层间隔靶的空间,又能达到有效的抗射流侵彻效果。
|
图 8 射流剩余头部速度随水夹层距离变化关系 Fig.8 The remaining jet tip velocity changing with distance of water interlayer |
射流剩余头部速度理论值与水夹层间隔靶结构变化关系三维曲面图如图 9所示。图中横轴分别代表水夹层间隔靶的结构变化因素,即靶板的厚度、水间隔的距离; 纵轴代表射流的剩余头部速度; 曲面上任一网格对应了不同结构水夹层间隔靶侵彻完成时射流的剩余头部速度。从图 9中可以看出,当靶板厚度小于20 mm,水间隔距离小于150 mm时,随着靶板厚度的增加,水间隔距离的增大,射流剩余头部速度减少趋势较明显。当至少一个结构变化因素不在该范围内时,随间隔靶厚度的增加,射流剩余头部速度减少趋势变缓慢。这说明当靶板厚度小于20 mm,且水间隔距离小于150 mm时,水夹层间隔靶对射流头部速度的衰减效率较高。在水夹层间隔靶设计时,要选择合适的靶板厚度和水间隔距离,兼顾水夹层间隔靶空间和抗射流侵彻效果。

|
图 9 射流穿过不同结构水夹层间隔靶后的剩余头部速度 Fig.9 The remaining jet tip velocity after spaced target with water interlayer penetrated |
(1) 结合准定常侵彻理论和数学归纳法建立了射流侵彻水夹层间隔靶理论模型,得到了射流头部速度与侵彻距离之间的关系。
(2) 设计了射流侵彻水夹层间隔靶实验,获得了侵彻过程中多个阶段的射流头部速度,与理论结果进行对比,最大误差为5.7%,平均误差为4.6%,验证了侵彻模型的正确性。
(3) 通过理论模型分析了靶板厚度和水间隔距离对射流侵彻水夹层间隔靶后剩余头部速度的影响。当靶板厚度小于20 mm,且水间隔距离小于150 mm时,水夹层间隔靶对射流头部速度的衰减效率较高。
| [1] |
Haugstad B S, Dullum O S. Finite compressibility in shaped charge jet and long rod penetration-the effect of shocks[J].
Journal of Applied Physics, 1981, 52(8): 5066-5071. DOI:10.1063/1.329450 |
| [2] |
Federov S V,Bayanova Ya M. Hydrodynamic model for penetration of extended projectiles with consideration of material compressibility[C]//Proc. 25th International Symposium on Ballistics,China,2010: 1032-1039.
|
| [3] |
Fils William J. A jet penetration model incorporating effects of compressibility and target strength[C]//The 12th Hypervelocity Impact Symposium(Procedia Engineering,2013 (58): 204 -213.
|
| [4] |
Oleg V. Svirsky, Nicolaip. Kovalev, Boris A. Klopov, et al. The shaped charge jet interaction with finite thickness targets[J].
International Journal of Impact Engineering, 2001, 26: 735-744. DOI:10.1016/S0734-743X(01)00123-3 |
| [5] |
Vlasov A S,Zilberbrand E L,Kozhushko A A,et al. Whipple shields against shaped charge jets[C]//Proc. 19th International Ballistics Symposium on Ballistics,Switzerland,2001: 1045-1051.
|
| [6] |
Horsfall I,Petrous E,Champion S M. Shaped charge attack of spaced and composite armor[C]//Proc. 23rd International Symposium on Ballistics,Spain,2007: 1281-1288.
|
| [7] |
Liu Beibei, Huang Zhengrong, Zu Xudong. Spaced armor effects on shaped charge jet penetration[J].
Propellants,Explosives,Pyrotechnics, 2015, 35: 1-7. |
| [8] |
张俊坤, 高欣宝, 熊冉, 等. 射流对间隙靶板屏蔽炸药的冲击起爆[J].
含能材料, 2014, 22(5): 607-611. ZHANG Jun-kun, GAO Xin-bao, XIONG Ran, et al. Jet impact initiation of the charge covered with spaced target[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2014, 22(5): 607-611. |
| [9] |
PEI Ming-jing, LI Cheng-bing. Experimental investigation of SCRSP penetrating the compound target with water interlayer[J].
Chinese Journal of Explosives & Propellants, 2008, 31(3): 15-19. |
| [10] |
张莉, 张庆明, 巨圆圆. 爆炸成型弹丸对含水复合装甲侵彻的实验研究[J].
北京理工大学学报, 2009, 29(3): 197-200. ZHANG Li, ZHANG Qing-ming, JU Yuan-yuan, et al. Experimental study on the penetration of explosively formed projectile against water-partitioned armor[J]. Transactions of Beijing Institute of Technology, 2009, 29(3): 197-200. |
| [11] |
Saroha D R,Singh Gurmit,Mahala V K. An experimental study of penetration behavior of shaped charge jets in water filled targets[C]//Proc. 24th International Symposium on Ballistics,USA,2008: 2-8.
|
| [12] |
Saroha D R,Kumar Davinder,Singh Yash Pal. Penetration behaviour simulation of shaped charge jets in water filled targets[C]//Proc. 26th International Symposium on Ballistics,USA,2011.
|
| [13] |
Max Peters. Development of techniques for investigation energy contributions to target deformation and penetration during reactive projectile hypervelocity impact[D]. Monterey California: Naval Postgraduate School,2011.
|
| [14] |
XING Shi-long, HUANG Xiang-ke. Simulation study on high-powered shaped warhead penetration into target with water layer[J].
Applied Mechanics and Materials, 2014, 532: 342-245. DOI:10.4028/www.scientific.net/AMM.532 |

The penetrating process of 50 mm caliber shaped charge penetrating spaced target with water interlayer (2 mm×4 mm steel plates +100 mm water interlayer) was studied through theoretical and experimental methods.




