Derived Ways of the Rate Equations of Autocatalytic Reaction and Their Application in Thermal Behavior Study of Energetic Materials
1 引言
含能材料(EM)体系自(动)催化反应的动力学行为和动力学三因子, 在EM对热抵抗能力的评估, 热爆炸临界温度、热爆炸临界温升速率、撞击感度(特性落高)、放热系统热感度、绝热至爆时间、燃烧速度的估算和放热分解反应诱导温度与诱导时间关系的定量描述方面扮演重要角色[1-6]。导出该类反应的速率方程、速率曲线方程和反应进度(α)随时间(t)和温度(T)变化的方程, 对描述、定量评估自催化反应的动力学行为, 有一定学术意义。本文依据EM体系自催化反应的特性: (1)自催化反应由催化剂生成反应和催化剂催化EM的催化反应组成, 体系自催化反应速率则是催化剂生成反应速率和催化反应速率的加和; (2)引导起始催化反应不能从反应进度α=0开始, 需要有催化产物; (3)具有催化功能的反应产物使反应经过一段诱导期后才能出现反应加速; (4)反应速率随某一催化反应产物浓度而增长; (5)自催化反应速率有最大值, 从α与反应能量变化的关系, 导出了经验级数自催化反应的速率方程。由经验级数自催化反应速率方程, 导出了13个自催化反应速率的派生式。由自催化反应特性(5)导出了描述自催化反应速率曲线特性[αmax和(dα/dt)max]的方程。通过速率方程的积分处理, 导出了α随t和T变化的方程。报道了描述六硝基六氮杂异伍兹烷(HNIW)自催化分解反应的速率方程和硝化棉(NC)(12.82%、12.97%、13.54%、13.61%、13.86%、13.88%、14.14% N)自催化分解反应的动力学参数—催化系数Kcat、速率曲线特性参数和α随t变化的方程。
2 理论和方法
2.1 经验级数自催化反应速率方程的导出途径
EM体系的自(动)催化反应由催化剂(B)的生成反应和催化剂催化EM的催化反应组成, 体系自催化反应速率则是催化剂生成反应速率和催化反应速率的加和。
由催化剂生成反应
|
$
m{\rm{EM}}\xrightarrow{{{k_{{\rm{CFR}}}}}}n{\rm{E}}{{\rm{M}}_{\rm{p}}} + {\rm{B}}
$
|
(1) |
和边界条件
|
$
\left. {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{l}}
{t = 0}\\
{t = t}\\
{t = \infty }
\end{array}}&{\begin{array}{*{20}{l}}
{{c_0}}\\
c\\
{{c_\infty } = 0}
\end{array}}&{\begin{array}{*{20}{l}}
{{\alpha _0} = 0}\\
\alpha \\
{{\alpha _\infty } = 1}
\end{array}}&\begin{array}{l}
0\\
{c_0} - c\\
{}
\end{array}&{\begin{array}{*{20}{l}}
{{Q_0} = 0}\\
Q\\
{{Q_\infty }}
\end{array}}
\end{array}} \right\}
$
|
(2) |
式(1)中, 下角标“p”代表产物; “CFR”代表催化剂生成反应。
知反应进度(α或c)与反应能量变化的关系[7]:
|
$
\frac{{{c_0} - c}}{{{c_0} - {c_\infty }}} = \frac{{{\alpha _0} - \alpha }}{{{\alpha _0} - {\alpha _\infty }}} = \frac{{{Q_0} - Q}}{{{Q_0} - {Q_\infty }}}
$
|
(3) |
|
$
\frac{{{c_0} - c}}{{{c_0}}} = \alpha = \frac{Q}{{{Q_\infty }}}
$
|
(4) |
|
$
c = {c_0}\left( {1 - \alpha } \right)
$
|
(5) |
|
$
{c_0} - c = {c_0}\alpha
$
|
(6) |
和催化剂生成速率方程的微分式
|
$
\frac{{{\rm{d}}\left( {{c_0} - c} \right)}}{{{\rm{d}}t}} = {k_{{\rm{CFR}}}}{c^m}
$
|
(7) |
|
$
{c_0}\frac{{{\rm{d}}\left( {\frac{{{c_0} - c}}{{{c_0}}}} \right)}}{{{\rm{d}}t}} = {k_{{\rm{CFR}}}}{\left[ {{c_0}\left( {1 - \alpha } \right)} \right]^m}
$
|
(8) |
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {k_{{\rm{CFR}}}}c_0^{m - 1}{\left( {1 - \alpha } \right)^m}
$
|
(9) |
令
|
$
{k_1} = {k_{{\rm{CFR}}}}c_0^{m - 1}
$
|
(10) |
则
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {k_1}{\left( {1 - \alpha } \right)^m}
$
|
(11) |
式中, c、α、Q和k有通常的含义。
由催化反应
|
$
\begin{gathered}
n{\rm{EM}} + {\rm{B}} \to n{\rm{EMB}} \hfill \\
\frac{{ + n{\rm{EMB}} + p{\rm{EM}} \to \left( {n + p} \right){\rm{E}}{{\rm{M}}_{\rm{p}}} + {\rm{B}}}}{{n{\rm{EM}} + p{\rm{EM}}\xrightarrow{{{k_{{\rm{CR}}}}}}\left( {n + p} \right){\rm{E}}{{\rm{M}}_{\rm{p}}}}} \hfill \\
\end{gathered}
$
|
(12) |
和边界条件
|
$
\left. {\begin{array}{*{20}{c}}
\begin{array}{l}
t = 0\\
t = t\\
t = \infty
\end{array}&\begin{array}{l}
\\
{c_0} - c\\
{}
\end{array}&\begin{array}{l}
{c_0}\\
c\\
{c_\infty } = 0
\end{array}&\begin{array}{l}
0\\
{c_0} - c\\
{}
\end{array}&\begin{array}{l}
{\alpha _0} = 0\\
\alpha \\
{\alpha _\infty } = 1
\end{array}&\begin{array}{l}
{Q_0} = 0\\
Q\\
{Q_\infty }
\end{array}
\end{array}} \right\}
$
|
(13) |
知方程(3)~(6)和催化反应速率方程的微分式
|
$
\frac{{{\rm{d}}\left( {{c_0} - c} \right)}}{{{\rm{d}}t}} = {k_{{\rm{CR}}}}{\left( {{c_0} - c} \right)^n}{c^p}
$
|
(14) |
|
$
\frac{{{c_0}}}{{{c_0}}}\frac{{{\rm{d}}\left( {{c_0} - c} \right)}}{{{\rm{d}}t}} = {k_{{\rm{CR}}}}{\left( {{c_0}\alpha } \right)^n}{\left[ {{c_0}\left( {1 - \alpha } \right)} \right]^p}
$
|
(15) |
|
$
{c_0}\frac{{{\rm{d}}\left( {\frac{{{c_0} - c}}{{{c_0}}}} \right)}}{{{\rm{d}}t}} = {k_{{\rm{CR}}}}c_0^{n + p}{\alpha ^n}{\left( {1 - \alpha } \right)^p}
$
|
(16) |
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {k_{{\rm{CR}}}}c_0^{n + p - 1}{\alpha ^n}{\left( {1 - \alpha } \right)^p}
$
|
(17) |
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {k_2}{\alpha ^n}{\left( {1 - \alpha } \right)^p}
$
|
(18) |
式中
|
$
{k_2} = {k_{{\rm{CR}}}}c_0^{n + p - 1}
$
|
(19) |
反应初期, α$ \ll $1, 式(18)可变为
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {k_2}{\alpha ^n}
$
|
(20) |
|
$
{\alpha ^{ - n}}{\rm{d}}\alpha = {k_2}{\rm{d}}t
$
|
(21) |
方程两边积分
|
$
\int {{\alpha ^{ - n}}{\rm{d}}\alpha } = \int {{k_2}{\rm{d}}t}
$
|
(22) |
得
|
$
\frac{{{\alpha ^{1 - n}}}}{{1 - n}} = {k_2} + {\rm{const}}
$
|
(23) |
据此不难看出, 引导起始反应不能从α=0开始, 需要有催化产物, 催化方程(18)应写为
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {k_2}{\left( {\alpha + {\alpha _0}} \right)^n}{\left( {1 - \alpha } \right)^p}
$
|
(24) |
考虑体系中还独立地进行着从k1(1-α)m速率给出催化产物的反应, 因此, 自催化方程应写为
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {k_1}{\left( {1 - \alpha } \right)^m} + {k_2}{\left( {\alpha + {\alpha _0}} \right)^n}{\left( {1 - \alpha } \right)^p}
$
|
(25) |
我们称式(25)为经验级数自催化反应速率方程。
2.2 经验级数自催化速率方程派生式的导出途径
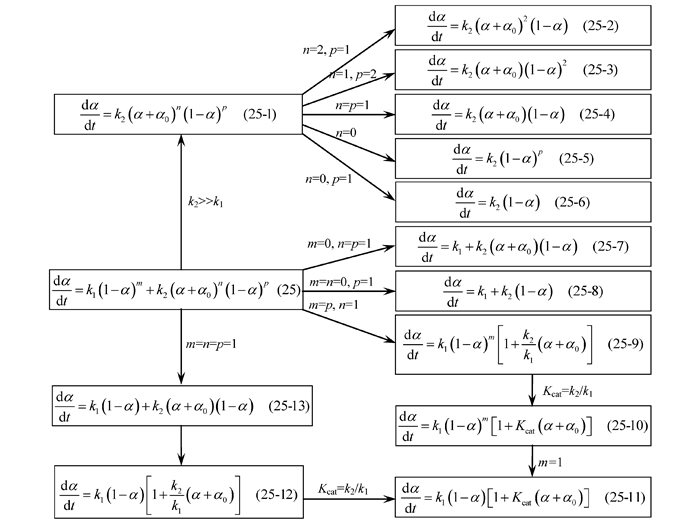
由经验级数(m、n、p)速率方程(25)导出的13个派生式见图 1。其中, 式(25-7)~(25-13)为自催化速率方程; 式(25-1)、(25-2)、(25-3)和(25-4)为催化速率方程; 式(25-2)、(25-3)和(25-4)分别称为第三类微分方程式、第二类微分方程式和第一类微分方程式。
式(25-10)和(25-11)中的Kcat称催化系数, 特指自催化方程dα/dt=k1(1-α)m+k2αn(1-α)p中k2与k1的比值:
|
$
{K_{{\rm{cat}}}} = \frac{{{k_2}}}{{{k_1}}} = \frac{{催化反应速率常数}}{{催化剂生成反应速率常数}}
$
|
对框图 1中各方程的参数:方程(25-2)、(25-3)、(25-4)和(25-6)中的2参数(A2、Ea2; A2、Ea2; A2、Ea2; A2、Ea2), 方程(25-5)和(25-11)中的3参数(A2、Ea2、p; A1、Ea1、Kcat), 方程(25-1)、(25-7)、(25-8)、(25-10)、(25-12)和(25-13)中的4参数(分别为A2、Ea2、n, p; A1、A2、Ea1、Ea2; A1、A2、Ea1、Ea2; A1、Ea1、m、Kcat; A1、A2、Ea1、Ea2; A1、A2、Ea1、Ea2), 方程(25-9)中的5参数(A1、A2、Ea1、Ea2、m)和方程(25)中的7参数(A1、A2、Ea1、Ea2、m、n、p)可用线性最小二乘法和信赖域方法求解[4-6, 8], 也可将方程(25-13)改写为
|
$
\frac{{{\rm{d}}y}}{{{\rm{d}}t}} = - {k_1}\left( T \right)y - {k_2}\left( T \right)y\left( {1 - y} \right)
$
|
和
|
$
\beta \frac{{{\rm{d}}y}}{{{\rm{d}}T}} = - \left[ {{k_1}\left( T \right) + {k_2}\left( T \right)} \right]y + {k_2}\left( T \right){y^2}
$
|
的形式, 通过解伯努利方程(Bernoulli方程), 得4参数(A1、A2、Ea1、Ea2)[9]。
这里, y是未反应物质的分数; 1-y是已发生反应物质的分数; T为温度; t为时间; k1(T)和k2(T)是一阶自催化方程在温度T的速率常数; k1(T)=A1exp(-E1/RT), k2(T)=A2exp(-E2/RT); 为指前因子; E为活化能; dt=dT/β, β是线性升温速率。
2.3 自催化反应速率曲线特性—αmax和(dα/dt)max —表达式的导出途径
由方程(25)两边对t求导
|
$
\begin{array}{l}
\frac{{{{\rm{d}}^2}\alpha }}{{{\rm{d}}{t^2}}} = {k_1}m{\left( {1 - \alpha } \right)^{m - 1}}\left( { - 1} \right)\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} + {k_2}n{\left( {\alpha + {\alpha _0}} \right)^{n - 1}}\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}{\left( {1 - \alpha } \right)^p} + \\
\;\;\;\;\;\;\;\;\;\;{k_2}{\left( {\alpha + {\alpha _0}} \right)^n}p{\left( {1 - \alpha } \right)^{p - 1}}\left( { - 1} \right)\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}\\
\;\;\;\;\;\;\;\; = \frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}\left[ { - {k_1}m{{\left( {1 - \alpha } \right)}^{m - 1}}{k_2}n{{\left( {\alpha + {\alpha _0}} \right)}^{n - 1}}{{\left( {1 - \alpha } \right)}^p} - } \right.\\
\;\;\;\;\;\;\;\;\;\;\left. {{k_2}p{{\left( {\alpha + {\alpha _0}} \right)}^n}{{\left( {1 - \alpha } \right)}^{p - 1}}} \right]
\end{array}
$
|
(26) |
和d2α/dt2=0, 速率达最大值, 得
|
$
\begin{array}{l}
{k_2}n{\left( {{\alpha _{\max }} + {\alpha _0}} \right)^{n - 1}}{\left( {1 - {\alpha _{\max }}} \right)^p}\\
= {k_1}m{\left( {1 - {\alpha _{\max }}} \right)^{m - 1}} + {k_2}p{\left( {{\alpha _{\max }} + {\alpha _0}} \right)^n}{\left( {1 - {\alpha _{\max }}} \right)^{p - 1}}
\end{array}
$
|
(27) |
由m=0, 得
|
$
{k_2}n{\left( {{\alpha _{\max }} + {\alpha _0}} \right)^{n - 1}}{\left( {1 - {\alpha _{\max }}} \right)^p} = {k_2}p{\left( {{\alpha _{\max }} + {\alpha _0}} \right)^n}{\left( {1 - {\alpha _{\max }}} \right)^{p - 1}}
$
|
(28) |
|
$
n\left( {1 - {\alpha _{\max }}} \right) = p\left( {{\alpha _{\max }} + {\alpha _0}} \right)
$
|
(29) |
|
$
n - n{\alpha _{\max }} = p{\alpha _{\max }} + p{\alpha _0}
$
|
(30) |
|
$
\left( {n + p} \right){\alpha _{\max }} = n - p{\alpha _0}
$
|
(31) |
|
$
{\alpha _{\max }} = \frac{{n - p{\alpha _0}}}{{n + p}}
$
|
(32) |
将αmax表达式(32)代入方程(25-1), 得
|
$
\begin{array}{l}
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_2}{\left( {{\alpha _{\max }} + {\alpha _0}} \right)^n}{\left( {1 - {\alpha _{\max }}} \right)^p}\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_2}{\left( {\frac{{n - p{\alpha _0}}}{{n + p}}} \right)^n}{\left( {1 - \frac{{n - p{\alpha _0}}}{{n + p}}} \right)^p}\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_2}{\left( {\frac{{n - p{\alpha _0} + n{\alpha _0} + p{\alpha _0}}}{{n + p}}} \right)^n}{\left( {\frac{{n + p - n + p{\alpha _0}}}{{n + p}}} \right)^p}\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_2}{\left[ {\frac{{n\left( {1 + {\alpha _0}} \right)}}{{n + p}}} \right]^n}{\left[ {\frac{{p\left( {1 + {\alpha _0}} \right)}}{{n + p}}} \right]^n}\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_2}{n^n}{p^p}{\left( {\frac{{1 + {\alpha _0}}}{{n + p}}} \right)^{n + p}}
\end{array}
$
|
(33) |
当α0$ \ll $1时
|
$
{\alpha _{\max }} = \frac{n}{{n + p}}
$
|
(34) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_2}{n^n}{p^p}{\left( {\frac{1}{{n + p}}} \right)^{n + p}}
$
|
(35) |
对n=2, p=1的派生式(25-2), 由式(32)和(33)知
|
$
{\alpha _{\max }} = \frac{{n - p{\alpha _0}}}{{n + p}} = \frac{{2 - {\alpha _0}}}{3}
$
|
(36) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_2}{n^n}{p^p}{\left( {\frac{{1 + {\alpha _0}}}{{n + p}}} \right)^{n + p}} = \frac{4}{{27}}{k_2}{\left( {1 + {\alpha _0}} \right)^3}
$
|
(37) |
当α0$ \ll $1时
|
$
{\alpha _{\max }} \approx \frac{2}{3}
$
|
(38) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} \approx \frac{4}{{27}}{k_2}
$
|
(39) |
对n=1, p=2的派生式(25-3), 由式(32)和(33)知
|
$
{\alpha _{\max }} = \frac{{n - p{\alpha _0}}}{{n + p}} = \frac{{1 - 2{\alpha _0}}}{3}
$
|
(40) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_2}{n^n}{p^p}{\left( {\frac{{1 + {\alpha _0}}}{{n + p}}} \right)^{n + p}} = \frac{4}{{27}}{k_2}{\left( {1 + {\alpha _0}} \right)^3}
$
|
(41) |
当α0$ \ll $1时
|
$
{\alpha _{\max }} \approx \frac{1}{3}
$
|
(42) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} \approx \frac{4}{{27}}{k_2}
$
|
(43) |
对n=p=1的派生式(25-4)
|
$
{\alpha _{\max }} = \frac{{n - p{\alpha _0}}}{{n + p}} = \frac{{1 - {\alpha _0}}}{2}
$
|
(44) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_2}{n^n}{p^p}{\left( {\frac{{1 + {\alpha _0}}}{{n + p}}} \right)^{n + p}} = \frac{1}{4}{k_2}{\left( {1 + {\alpha _0}} \right)^2}
$
|
(45) |
当α0$ \ll $1时
|
$
{\alpha _{\max }} \approx \frac{1}{2}
$
|
(46) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} \approx \frac{1}{4}{k_2}
$
|
(47) |
对m=0, n=p=1的派生式(25-7), 由式(27)知
|
$
{k_2}\left( {1 - {\alpha _{\max }}} \right) = {k_2}\left( {{\alpha _{\max }} + {\alpha _0}} \right)
$
|
(48) |
|
$
\begin{array}{l}
1 - {\alpha _{\max }} = {\alpha _{\max }} + {\alpha _0}\\
\;\;\;1 - {\alpha _0} = 2{\alpha _{\max }}\\
\;\;\;\;\;{\alpha _{\max }} = \frac{{1 - {\alpha _0}}}{2}
\end{array}
$
|
(49) |
|
$
\begin{array}{l}
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_1} + {k_2}\left( {{\alpha _{\max }} + {\alpha _0}} \right)\left( {1 - {\alpha _{\max }}} \right)\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_1} + {k_2}\left( {\frac{{1 - {\alpha _0}}}{2} + {\alpha _0}} \right)\left( {1 - \frac{{1 - {\alpha _0}}}{2}} \right)\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_1} + {k_2}\left( {\frac{{1 - {\alpha _0} + 2{\alpha _0}}}{2}} \right)\left( {\frac{{1 + {\alpha _0}}}{2}} \right)\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_1} + {k_2}{\left( {\frac{{1 + {\alpha _0}}}{2}} \right)^2}
\end{array}
$
|
(50) |
当α0$ \ll $1时
|
$
{\alpha _{\max }} \approx \frac{1}{2}
$
|
(51) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} \approx {k_1} + \frac{1}{4}{k_2}
$
|
(52) |
对m=n=0, p=1的派生式(25-8), 由式(27)知
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_1} + {k_2}\left( {1 - {\alpha _{\max }}} \right) = {k_1}
$
|
(54) |
对m=n=p=1的派生式(25-13), 由式(27)知
|
$
{{k_2}\left( {1 - {\alpha _{\max }}} \right) = {k_1} + {k_2}\left( {{\alpha _{\max }} + {\alpha _0}} \right)}
$
|
(55) |
|
$
\begin{array}{l}
{k_2} - {k_2}{\alpha _{\max }} = {k_1} + {k_2}{\alpha _{\max }} + {k_2}{\alpha _0}\\
\;\;\;\;2{k_2}{\alpha _{\max }} = {k_2} - {k_1} - {k_2}{\alpha _0}\\
\;\;\;\;\;\;\;\;\;{\alpha _{\max }} = \frac{{{k_2}\left( {1 - {\alpha _0}} \right) - {k_1}}}{{2{k_2}}}
\end{array}
$
|
(56) |
|
$
\begin{array}{*{20}{l}}
{{{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)}_{\max }} = {k_1}\left( {1 - {\alpha _{\max }}} \right) + {k_2}\left( {{\alpha _{\max }} + {\alpha _0}} \right)\left( {1 - {\alpha _{\max }}} \right)}\\
{\;\;\;\;\;\;\;\;\;\;\;\;\; = \left( {1 - {\alpha _{\max }}} \right)\left[ {{k_1} + {k_2}\left( {{\alpha _{\max }} + {\alpha _0}} \right)} \right]}
\end{array}
$
|
(57) |
令Kcat=k2/k1, 则
|
$
\begin{array}{l}
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_1}\left( {1 - {\alpha _{\max }}} \right)\left[ {1 + {K_{{\rm{cat}}}}\left( {{\alpha _{\max }} + {\alpha _0}} \right)} \right]\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_1}\left[ {1 - \frac{{{k_2}\left( {1 - {\alpha _0}} \right) - {k_1}}}{{2{k_2}}}} \right]\left\{ {1 + {K_{{\rm{cat}}}}\left[ {\frac{{{k_2}\left( {1 - {\alpha _0}} \right) - {k_1}}}{{2{k_2}}} + {\alpha _0}} \right]} \right\}\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_1}\left( {1 - \frac{{{k_2} - {k_2}{\alpha _0} - {k_1}}}{{2{k_2}}}} \right)\left[ {1 + {K_{{\rm{cat}}}}\left( {\frac{{{k_2} - {k_2}{\alpha _0} - {k_1}}}{{2{k_2}}} + {\alpha _0}} \right)} \right]\\
\;\;\;\;\;\;\;\;\;\;\;\;\; = {k_1}\left[ {\frac{{{k_2}\left( {1 + {\alpha _0}} \right) + {k_1}}}{{2{k_2}}}} \right]\left\{ {1 + {K_{{\rm{cat}}}}\left[ {\frac{{{k_2}\left( {1 + {\alpha _0}} \right) - {k_1}}}{{2{k_2}}}} \right]} \right\}
\end{array}
$
|
(58) |
当α0$ \ll $1时
|
$
{\alpha _{\max }} \approx \frac{{{k_2} - {k_1}}}{{2{k_2}}}
$
|
(59) |
|
$
{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{\max }} = {k_1}\left( {\frac{{{k_2} + {k_1}}}{{2{k_2}}}} \right)\left[ {1 + {K_{{\rm{cat}}}}\left( {\frac{{{k_2} - {k_1}}}{{2{k_2}}}} \right)} \right]
$
|
(60) |
2.4 自催化反应的α随t变化方程的导出途径
对方程(25-13), 由
|
$
\int_0^\alpha {\frac{1}{{{k_1}\left( {1 - \alpha } \right) + {k_2}\left( {\alpha + {\alpha _0}} \right)\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(61) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_1}\left( {1 - \alpha } \right) + {k_2}\left( {\alpha + {\alpha _0}} \right)\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \int_0^\alpha {\left\{ {\frac{1}{{\left[ {{k_1} + {k_2}\left( {1 + {\alpha _0}} \right)} \right]\left( {1 - \alpha } \right)}} + \frac{{{k_2}}}{{\left[ {{k_1} + {k_2}\left( {1 + {\alpha _0}} \right)} \right]\left[ {{k_1} + {k_2}\left( {\alpha + {\alpha _0}} \right)} \right]}}} \right\}{\rm{d}}\alpha } \\
= \frac{1}{{{k_1} + {k_2}\left( {1 + {\alpha _0}} \right)}}\int_0^\alpha {\left\{ {\frac{1}{{1 - \alpha }} + \frac{{{k_2}}}{{{k_1} + {k_2}\left( {\alpha + {\alpha _0}} \right)}}} \right\}{\rm{d}}\alpha } \\
= \frac{1}{{{k_1} + {k_2}\left( {1 + {\alpha _0}} \right)}}\left\{ { - \ln \left( {1 - \alpha } \right) + \ln \left[ {{k_1} + {k_2}\left( {\alpha + {\alpha _0}} \right)} \right]} \right\}\left| {_0^\alpha } \right.\\
= \frac{1}{{{k_1} + {k_2}\left( {1 + {\alpha _0}} \right)}}\left\{ { - \ln \left( {1 - \alpha } \right) + \ln \left[ {{k_1} + {k_2}\left( {\alpha + {\alpha _0}} \right)} \right] - \ln \left( {{k_1} + {k_2}{\alpha _0}} \right)} \right\}\\
= \frac{1}{{{k_1} + {k_2}\left( {1 + {\alpha _0}} \right)}}\ln \frac{{{k_1} + {k_2}\left( {\alpha + {\alpha _0}} \right)}}{{\left( {1 - \alpha } \right)\left( {{k_1} + {k_2}{\alpha _0}} \right)}}
\end{array}
$
|
(62) |
得
|
$
\frac{1}{{{k_1} + {k_2}\left( {1 + {\alpha _0}} \right)}}\ln \frac{{{k_1} + {k_2}\left( {\alpha + {\alpha _0}} \right)}}{{\left( {1 - \alpha } \right)\left( {{k_1} + {k_2}{\alpha _0}} \right)}} = t
$
|
(63) |
|
$
\frac{{{k_1} + {k_2}\left( {\alpha + {\alpha _0}} \right)}}{{\left( {1 - \alpha } \right)\left( {{k_1} + {k_2}{\alpha _0}} \right)}} = {{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0 } \right)} \right]t}}
$
|
(64) |
|
$
{k_1} + {k_2}\left( {\alpha + {\alpha _0}} \right) = \left( {1 - \alpha } \right)\left( {{k_1} + {k_2}{\alpha _0}} \right){{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 - \alpha_0} \right)} \right]t}}
$
|
(65) |
|
$
\begin{array}{l}
{k_1} + {k_2}{\alpha _0} + {k_2}\alpha = \left( {{k_1} + {k_2}{\alpha _0}} \right){{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}} - \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{k_1} + {k_2}{\alpha _0}} \right)\alpha {{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}}
\end{array}
$
|
(66) |
|
$
\begin{array}{l}
{k_2}\alpha + \left( {{k_1} + {k_2}{\alpha _0}} \right)\alpha {{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}}\\
= \left( {{k_1} + {k_2}{\alpha _0}} \right){{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}} - \left( {{k_1} + {k_2}{\alpha _0}} \right)
\end{array}
$
|
(67) |
|
$
\alpha = \left( {{k_1} + {k_2}{\alpha _0}} \right)\frac{{{{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}} - 1}}{{{k_2} + \left( {{k_1} + {k_2}{\alpha _0}} \right){{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}}}}
$
|
(68) |
|
$
\alpha = \frac{{\left( {{k_1} + {k_2}{\alpha _0}} \right)\left[ {{{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}} - 1} \right] + \left( {{k_2} - {k_2}} \right)}}{{{k_2} + \left( {{k_1} + {k_2}{\alpha _0}} \right){{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}}}}
$
|
(69) |
|
$
\alpha = 1 - \frac{{{k_1} + {k_2}\left( {1 + {\alpha _0}} \right)}}{{\left( {{k_1} + {k_2}{\alpha _0}} \right){{\rm{e}}^{\left[ {{k_1} + {k_2}\left( {1 + \alpha_0} \right)} \right]t}} + {k_2}}}
$
|
(70) |
对α0=0.0001≈0的方程(25-13), 由
|
$
\int_0^\alpha {\frac{1}{{{k_1}\left( {1 - \alpha } \right) + {k_2}\alpha \left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(71) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_1}\left( {1 - \alpha } \right) + {k_2}\alpha \left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \int_0^\alpha {\left[ {\frac{1}{{\left( {{k_1} + {k_2}} \right)\left( {1 - \alpha } \right)}} + \frac{{{k_2}}}{{\left( {{k_1} + {k_2}} \right)\left( {{k_1} + {k_2}\alpha } \right)}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{k_1} + {k_2}}}\int_0^\alpha {\left( {\frac{1}{{1 - \alpha }} + \frac{{{k_2}}}{{{k_1} + {k_2}\alpha }}} \right){\rm{d}}\alpha } \\
= \frac{1}{{{k_1} + {k_2}}}\left[ { - \ln \left( {1 - \alpha } \right) + \ln \left( {{k_1} + {k_2}\alpha } \right)} \right]\left| {_0^\alpha } \right.\\
= \frac{1}{{{k_1} + {k_2}}}\left[ { - \ln \left( {1 - \alpha } \right) + \ln \left( {{k_1} + {k_2}\alpha } \right) - \ln {k_1}} \right]\\
= \frac{1}{{{k_1} + {k_2}}}\ln \frac{{{k_1} + {k_2}\alpha }}{{{k_1}\left( {1 - \alpha } \right)}}
\end{array}
$
|
(72) |
得
|
$
\frac{1}{{{k_1} + {k_2}}}\ln \frac{{{k_1} + {k_2}\alpha }}{{{k_1}\left( {1 - \alpha } \right)}}t
$
|
(73) |
|
$
\frac{{{k_1} + {k_2}\alpha }}{{{k_1}\left( {1 - \alpha } \right)}} = {{\rm{e}}^{\left( {{k_1} + {k_2}} \right)t}}
$
|
(74) |
|
$
{k_1} + {k_2}\alpha = {k_1}\left( {1 - \alpha } \right){{\rm{e}}^{\left( {{k_1} + {k_2}} \right)t}}
$
|
(75) |
|
$
{k_2}\alpha + {k_1}\alpha {{\rm{e}}^{\left( {{k_1} + {k_2}} \right)t}} = {k_1}{{\rm{e}}^{\left( {{k_1} + {k_2}} \right)t}} - {k_1}
$
|
(76) |
|
$
\alpha = \frac{{{k_1}{{\rm{e}}^{\left( {{k_1} + {k_2}} \right)t}} - {k_1}}}{{{k_1}{{\rm{e}}^{\left( {{k_1} + {k_2}} \right)t}} + {k_2}}}
$
|
(77) |
|
$
\alpha = 1 - \frac{{{k_1} + {k_2}}}{{{k_1}{{\rm{e}}^{\left( {{k_1} + {k_2}} \right)t}} + {k_2}}}
$
|
(78) |
对方程(25-8), 由
|
$
\int_0^\alpha {\frac{1}{{{k_1} + {k_2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(79) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_1} + {k_2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \int_0^\alpha {\frac{1}{{{k_1} + {k_2}\left( {1 - \alpha } \right)}}\frac{{ - 1}}{{{k_2}}}{\rm{d}}\left[ {{k_1} + {k_2}\left( {1 - \alpha } \right)} \right]} \\
= - \frac{1}{{{k_2}}}\ln \left[ {{k_1} + {k_2}\left( {1 - \alpha } \right)} \right]\left| {_0^\alpha } \right.\\
= - \frac{1}{{{k_2}}}\left\{ {\ln \left[ {{k_1} + {k_2}\left( {1 - \alpha } \right)} \right] - \ln \left( {{k_1} + {k_2}} \right)} \right\}\\
= - \frac{1}{{{k_2}}}\ln \frac{{{k_1} + {k_2}\left( {1 - \alpha } \right)}}{{{k_1} + {k_2}}}
\end{array}
$
|
(80) |
|
$
\int_0^t {{\rm{d}}t} = t
$
|
(81) |
得
|
$
- \frac{1}{{{k_2}}}\ln \frac{{{k_1} + {k_2}\left( {1 - \alpha } \right)}}{{{k_1} + {k_2}}} = t
$
|
(82) |
|
$
\ln \frac{{{k_1} + {k_2}\left( {1 - \alpha } \right)}}{{{k_1} + {k_2}}} = - {k_2}t
$
|
(83) |
|
$
\frac{{{k_1} + {k_2}\left( {1 - \alpha } \right)}}{{{k_1} + {k_2}}} = {{\rm{e}}^{ - {k_2}t}}
$
|
(84) |
|
$
{k_1} + {k_2}\left( {1 - \alpha } \right) = \left( {{k_1} + {k_2}} \right){{\rm{e}}^{ - {k_2}t}}
$
|
(85) |
|
$
\alpha = \frac{{{k_1} + {k_2}}}{{{k_2}}}\left( {1 - {{\rm{e}}^{ - {k_2}t}}} \right)
$
|
(86) |
对方程(25-11), 由
|
$
\int_0^\alpha {\frac{1}{{{k_1}\left( {1 - \alpha } \right)\left[ {1 + {K_{{\rm{cat}}}}\left( {\alpha + {\alpha _0}} \right)} \right]}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(87) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_1}\left( {1 - \alpha } \right)\left[ {1 + {K_{{\rm{cat}}}}\left( {\alpha + {\alpha _0}} \right)} \right]}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_1}}}\int_0^\alpha {\left[ {\frac{1}{{\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)\left( {1 - \alpha } \right)}} + \frac{{{K_{{\rm{cat}}}}}}{{\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)\left( {1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0}} \right)}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)}}\int_0^\alpha {\left( {\frac{1}{{1 - \alpha }} + \frac{{{K_{{\rm{cat}}}}}}{{1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0}}}} \right){\rm{d}}\alpha } \\
= \frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)}}\left[ { - \ln \left( {1 - \alpha } \right) + \ln \left( {1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0}} \right)} \right]\left| {_0^\alpha } \right.\\
= \frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)}}\left[ { - \ln \left( {1 - \alpha } \right) + \ln \left( {1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0}} \right) - \ln \left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right)} \right]\\
= \frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)}}\ln \frac{{1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0}}}{{\left( {1 - \alpha } \right)\left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right)}}
\end{array}
$
|
(88) |
得
|
$
\frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)}}\ln \frac{{1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0}}}{{\left( {1 - \alpha } \right)\left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right)}} = t
$
|
(89) |
|
$
\ln \frac{{1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0}}}{{\left( {1 - \alpha } \right)\left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right)}} = {k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t
$
|
(90) |
|
$
1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0} = \left( {1 - \alpha } \right)\left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right){{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t}}
$
|
(91) |
|
$
\begin{array}{l}
1 + {K_{{\rm{cat}}}}\alpha + {K_{{\rm{cat}}}}{\alpha _0} = \left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right){{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t}} - \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right){{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t}}\alpha
\end{array}
$
|
(92) |
|
$
\begin{array}{l}
{K_{{\rm{cat}}}}\alpha + \left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right){{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t}}\alpha \\
= \left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right){{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t}} - \left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right)
\end{array}
$
|
(93) |
|
$
\begin{array}{l}
\alpha = \frac{{\left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right)\left[ {{{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t}} - 1} \right]}}{{{K_{{\rm{cat}}}} + \left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right){{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t}}}}\\
\;\;\; = 1 - \frac{{{K_{{\rm{cat}}}} + \left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right)}}{{{K_{{\rm{cat}}}} + \left( {1 + {K_{{\rm{cat}}}}{\alpha _0}} \right){{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}} + {K_{{\rm{cat}}}}{\alpha _0}} \right)t}}}}
\end{array}
$
|
(94) |
对α0=0.0001≈0的方程(25-11), 由
|
$
\int_0^\alpha {\frac{1}{{{k_1}\left( {1 - \alpha } \right)\left( {1 + {K_{{\rm{cat}}}}\alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(95) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_1}\left( {1 - \alpha } \right)\left( {1 + {K_{{\rm{cat}}}}\alpha } \right)}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_1}}}\int_0^\alpha {\left[ {\frac{1}{{\left( {1 + {K_{{\rm{cat}}}}} \right)\left( {1 - \alpha } \right)}} + \frac{{{K_{{\rm{cat}}}}}}{{\left( {1 + {K_{{\rm{cat}}}}} \right)\left( {1 + {K_{{\rm{cat}}}}\alpha } \right)}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)}}\int_0^\alpha {\left( {\frac{1}{{1 - \alpha }} + \frac{{{K_{{\rm{cat}}}}}}{{1 + {K_{{\rm{cat}}}}\alpha }}} \right){\rm{d}}\alpha } \\
= \frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)}}\left[ { - \ln \left( {1 - \alpha } \right) + \ln \left( {1 + {K_{{\rm{cat}}}}\alpha } \right)} \right]\left| {_0^\alpha } \right.\\
= \frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)}}\left[ { - \ln \left( {1 - \alpha } \right) + \ln \left( {1 + {K_{{\rm{cat}}}}\alpha } \right)} \right]\\
= \frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)}}\ln \frac{{1 + {K_{{\rm{cat}}}}\alpha }}{{1 - \alpha }}
\end{array}
$
|
(96) |
得
|
$
\frac{1}{{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)}}\ln \frac{{1 + {K_{{\rm{cat}}}}\alpha }}{{1 - \alpha }} = t
$
|
(97) |
|
$
\ln \frac{{1 + {K_{{\rm{cat}}}}\alpha }}{{1 - \alpha }} = {k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t
$
|
(98) |
|
$
1 + {K_{{\rm{cat}}}}\alpha = \left( {1 - \alpha } \right){{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t}}
$
|
(99) |
|
$
1 + {K_{{\rm{cat}}}}\alpha = {{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t}} - {{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t}}\alpha
$
|
(100) |
|
$
{K_{{\rm{cat}}}}\alpha = {{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t}}\alpha = {{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t}} - 1
$
|
(101) |
|
$
\alpha = \frac{{{{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t}} - 1}}{{{K_{{\rm{cat}}}} + {{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t}}}} = 1 - \frac{{{K_{{\rm{cat}}}} + 1}}{{{K_{{\rm{cat}}}} + {{\rm{e}}^{{k_1}\left( {1 + {K_{{\rm{cat}}}}} \right)t}}}}
$
|
(102) |
对方程(25-4), 由
|
$
\int_0^\alpha {\frac{1}{{{k_2}\left( {\alpha + {\alpha _0}} \right)\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(103) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_2}\left( {\alpha + {\alpha _0}} \right)\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}\left( {{\alpha _0} + 1} \right)}}\int_0^\alpha {\left( {\frac{1}{{\alpha + {\alpha _0}}} + \frac{1}{{1 - \alpha }}} \right){\rm{d}}\alpha } \\
= \frac{1}{{{k_2}\left( {{\alpha _0} + 1} \right)}}\left[ {\ln \left( {\alpha + {\alpha _0}} \right) - \ln \left( {1 - \alpha } \right)} \right]\left| {_0^\alpha } \right.\\
= \frac{1}{{{k_2}\left( {{\alpha _0} + 1} \right)}}\left[ {\ln \left( {\alpha + {\alpha _0}} \right) - \ln \left( {1 - \alpha } \right) - \ln {\alpha _0}} \right]\\
= \frac{1}{{{k_2}\left( {{\alpha _0} + 1} \right)}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}
\end{array}
$
|
(104) |
得
|
$
\frac{1}{{{k_2}\left( {{\alpha _0} + 1} \right)}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = t
$
|
(105) |
|
$
\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = {k_2}\left( {{\alpha _0} + 1} \right)t
$
|
(106) |
|
$
\alpha + {\alpha _0} = {\alpha _0}\left( {1 - \alpha } \right){{\rm{e}}^{{k_2}\left( {{\alpha _0} + 1} \right)t}}
$
|
(107) |
|
$
\left[ {1 + {\alpha _0}{{\rm{e}}^{{k_2}\left( {{\alpha _0} + 1} \right)t}}} \right]\alpha = {\alpha _0}\left[ {{{\rm{e}}^{{k_2}\left( {{\alpha _0} + 1} \right)t}} - 1} \right]
$
|
(108) |
|
$
\alpha = \frac{{{\alpha _0}\left[ {{{\rm{e}}^{{k_2}\left( {{\alpha _0} + 1} \right)t}} - 1} \right]}}{{1 + {\alpha _0}{{\rm{e}}^{{k_2}\left( {{\alpha _0} + 1} \right)t}}}} = 1 - \frac{{1 + {\alpha _0}}}{{1 + {\alpha _0}{{\rm{e}}^{{k_2}\left( {{\alpha _0} + 1} \right)t}}}}
$
|
(109) |
反应初期, α0$ \ll $1
|
$
\alpha = {\alpha _0}\left[ {{{\rm{e}}^{{k_2}\left( {{\alpha _0} + 1} \right)t}} - 1} \right] \approx {\alpha _0}{{\rm{e}}^{{k_2}\left( {{\alpha _0} + 1} \right)t}}
$
|
(110) |
显示反应随时间呈指数变化的规律。
对α0$ \ll $1, α0=0.0001≈0的方程(25-4), 由
|
$
\int_{0.0001}^\alpha {\frac{1}{{{k_2}\alpha \left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(111) |
知
|
$
\begin{array}{l}
\int_{0.0001}^\alpha {\frac{1}{{{k_2}\alpha \left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\int_{0.0001}^\alpha {\left( {\frac{1}{\alpha } + \frac{1}{{1 - \alpha }}} \right){\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\left[ {\ln \alpha - \ln \left( {1 - \alpha } \right)} \right]\left| {_{0.0001}^\alpha } \right.\\
= \frac{1}{{{k_2}}}\left[ {\ln \alpha - \ln \left( {1 - \alpha } \right) - \ln 0.0001 + \ln \left( {1 - 0.0001} \right)} \right]\\
= \frac{1}{{{k_2}}}\ln \frac{{9999\alpha }}{{1 - \alpha }}
\end{array}
$
|
(112) |
得
|
$
\frac{1}{{{k_2}}}\ln \frac{{9999\alpha }}{{1 - \alpha }} = t
$
|
(113) |
|
$
\ln \frac{{9999\alpha }}{{1 - \alpha }} = {k_2}t
$
|
(114) |
|
$
9999\alpha = \left( {1 - \alpha } \right){{\rm{e}}^{{k_2}t}}
$
|
(115) |
|
$
\left( {9999 + {{\rm{e}}^{{k_2}t}}} \right)\alpha = {{\rm{e}}^{{k_2}t}}
$
|
(116) |
|
$
\alpha = \frac{{{{\rm{e}}^{{k_2}t}}}}{{9999 + {{\rm{e}}^{{k_2}t}}}} = 1 - \frac{{9999}}{{{{\rm{e}}^{{k_2}t}}}}
$
|
(117) |
对方程(25-2), 由
|
$
\int_0^\alpha {\frac{1}{{{k_2}{{\left( {\alpha + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(118) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_2}{{\left( {\alpha + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\int_0^\alpha {\frac{{{{\left( {1 - {\alpha _0}} \right)}^2}}}{{{{\left( {1 + {\alpha _0}} \right)}^2}{{\left( {\alpha + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\int_0^\alpha {\left[ {\frac{1}{{\left( {1 + {\alpha _0}} \right){{\left( {\alpha + {\alpha _0}} \right)}^2}}} + \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}} + \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}\left( {\alpha + {\alpha _0}} \right)}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\left[ { - \frac{1}{{\left( {1 + {\alpha _0}} \right)\left( {\alpha + {\alpha _0}} \right)}} - \frac{{\ln \left( {1 - \alpha } \right)}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}} + \frac{{\ln \left( {\alpha + {\alpha _0}} \right)}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}} \right]\left| {_0^\alpha } \right.\\
= \frac{1}{{{k_2}}}\left[ { - \frac{1}{{\left( {1 + {\alpha _0}} \right)\left( {\alpha + {\alpha _0}} \right)}} - \frac{{\ln \left( {1 - \alpha } \right)}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}} + \frac{{\ln \left( {\alpha + {\alpha _0}} \right)}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}} + \frac{1}{{\left( {1 + {\alpha _0}} \right){\alpha _0}}} - \frac{{\ln {\alpha _0}}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}} \right]\\
= \frac{1}{{{k_2}}}\left[ {\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{\left( {1 + {\alpha _0}} \right){\alpha _0}}} - \frac{1}{{\left( {1 + {\alpha _0}} \right)\left( {\alpha + {\alpha _0}} \right)}}} \right]\\
= \frac{1}{{{k_2}\left( {1 + {\alpha _0}} \right)}}\left[ {\frac{1}{{\left( {1 + {\alpha _0}} \right)}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right]
\end{array}
$
|
(119) |
得
|
$
\frac{1}{{{k_2}\left( {1 + {\alpha _0}} \right)}}\left[ {\frac{1}{{\left( {1 + {\alpha _0}} \right)}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right] = t
$
|
(120) |
对α0$ \ll $1, α0=0.0001≈0的方程(25-2), 由
|
$
\int_{0.0001}^\alpha {\frac{1}{{{k_2}{\alpha ^2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(121) |
知
|
$
\begin{array}{l}
\int_{0.0001}^\alpha {\frac{1}{{{k_2}{\alpha ^2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\int_{0.0001}^\alpha {\left( {\frac{1}{{{\alpha ^2}}} + \frac{1}{\alpha } + \frac{1}{{1 - \alpha }}} \right){\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\left[ { - \frac{1}{\alpha } + \ln \alpha - \ln \left( {1 - \alpha } \right)} \right]\left| {_{0.0001}^\alpha } \right.\\
= \frac{1}{{{k_2}}}\left[ { - \frac{1}{\alpha } + \ln \alpha - \ln \left( {1 - \alpha } \right) + 10000 - \ln 0.0001 + \ln \left( {1 - 0.0001} \right)} \right]\\
= \frac{1}{{{k_2}}}\left( { - \frac{1}{\alpha } + \ln \frac{{9999\alpha }}{{1 - \alpha }} + 10000} \right)
\end{array}
$
|
(122) |
得
|
$
\frac{1}{{{k_2}}}\left( { - \frac{1}{\alpha } + \ln \frac{{9999\alpha }}{{1 - \alpha }} + 10000} \right) = t
$
|
(123) |
|
$
\frac{1}{{{k_2}}}\left( { - \frac{1}{\alpha } + \ln \frac{{9999\alpha }}{{1 - \alpha }} + 10000} \right) = t
$
|
(124) |
|
$
- \frac{1}{\alpha } + \ln \frac{{9999\alpha }}{{1 - \alpha }} + 10000 = {k_2}t
$
|
(125) |
对方程(25-3), 由
|
$
\int_0^\alpha {\frac{1}{{{k_2}\left( {\alpha + {\alpha _0}} \right){{\left( {1 - \alpha } \right)}^2}}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(126) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_2}\left( {\alpha + {\alpha _0}} \right){{\left( {1 - \alpha } \right)}^2}}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\int_0^\alpha {\left[ {\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}} + \frac{1}{{\left( {1 + {\alpha _0}} \right){{\left( {1 - \alpha } \right)}^2}}} + \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}\left( {\alpha + {\alpha _0}} \right)}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}{{\left( {1 + {\alpha _0}} \right)}^2}}}\int_0^\alpha {\left[ {\frac{1}{{1 - \alpha }} + \frac{{1 + {\alpha _0}}}{{{{\left( {1 - \alpha } \right)}^2}}} + \frac{1}{{\alpha + {\alpha _0}}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ { - \ln \left( {1 - \alpha } \right) + \frac{{1 + {\alpha _0}}}{{1 - \alpha }} + \ln \left( {\alpha + {\alpha _0}} \right)} \right]\left| {_0^\alpha } \right.\\
= \frac{1}{{{k_2}{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ { - \ln \left( {1 - \alpha } \right) + \frac{{1 + {\alpha _0}}}{{1 - \alpha }} + \ln \left( {\alpha + {\alpha _0}} \right) - \left( {1 + {\alpha _0}} \right) - \ln {\alpha _0}} \right]\\
= \frac{1}{{{k_2}{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{\alpha \left( {1 + {\alpha _0}} \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right]
\end{array}
$
|
(127) |
得
|
$
\frac{1}{{{k_2}{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{\alpha \left( {1 + {\alpha _0}} \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right] = t
$
|
(128) |
|
$
\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = {k_2}{\left( {1 + {\alpha _0}} \right)^2}t - \frac{{\alpha \left( {1 + {\alpha _0}} \right)}}{{1 - \alpha }}
$
|
(129) |
对α0$ \ll $1, α0=0.0001≈0的方程(25-3), 由
|
$
\int_{0.0001}^\alpha {\frac{1}{{{k_2}\alpha {{\left( {1 - \alpha } \right)}^2}}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(130) |
知
|
$
\begin{array}{l}
\int_{0.0001}^\alpha {\frac{1}{{{k_2}\alpha {{\left( {1 - \alpha } \right)}^2}}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\int_{0.0001}^\alpha {\frac{1}{{\alpha {{\left( {1 - \alpha } \right)}^2}}}{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\int_{0.0001}^\alpha {\left[ {\frac{1}{\alpha } + \frac{1}{{1 - \alpha }} + \frac{1}{{{{\left( {1 - \alpha } \right)}^2}}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{k_2}}}\left[ {\ln \alpha - \ln \left( {1 - \alpha } \right) + \frac{1}{{1 - \alpha }}} \right]\left| {_{0.0001}^\alpha } \right.\\
= \frac{1}{{{k_2}}}\left[ {\ln \alpha - \ln \left( {1 - \alpha } \right) + \frac{1}{{1 - \alpha }} - \ln 0.0001 + \ln \left( {1 - 0.0001} \right) - \frac{1}{{1 - 0.0001}}} \right]\\
= \frac{1}{{{k_2}}}\left( {\frac{1}{{1 - \alpha }} + \ln \frac{{9999\alpha }}{{1 - \alpha }} - \frac{{10000}}{{9999}}} \right)
\end{array}
$
|
(131) |
得
|
$
\frac{1}{{{k_2}}}\left( {\frac{1}{{1 - \alpha }} + \ln \frac{{9999\alpha }}{{1 - \alpha }} - \frac{{10000}}{{9999}}} \right) = t
$
|
(132) |
|
$
\frac{1}{{1 - \alpha }} + \ln \frac{{9999\alpha }}{{1 - \alpha }} - \frac{{10000}}{{9999}} = {k_2}t
$
|
(133) |
|
$
\ln \frac{{9999\alpha }}{{1 - \alpha }} = {k_2}t - \frac{1}{{1 - a}} + \frac{{10000}}{{9999}}
$
|
(134) |
对方程(25-5), 由
|
$
\int_0^\alpha {\frac{1}{{{k_2}{{\left( {1 - \alpha } \right)}^p}}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(135) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_2}{{\left( {1 - \alpha } \right)}^p}}}{\rm{d}}\alpha } = \frac{1}{{{k_2}}}\int_0^\alpha {\frac{1}{{{{\left( {1 - \alpha } \right)}^p}}}{\rm{d}}\alpha } \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{{{k_2}}}\frac{{{{\left( {1 - \alpha } \right)}^{1 - p}} - 1}}{{p - 1}}
\end{array}
$
|
(136) |
得
|
$
\frac{1}{{{k_2}}}\frac{{{{\left( {1 - \alpha } \right)}^{1 - p}} - 1}}{{p - 1}} = t
$
|
(137) |
|
$
\begin{array}{l}
\\
{\left( {1 - \alpha } \right)^{1 - p}} = \left( {p - 1} \right){k_2}t + 1
\end{array}
$
|
(138) |
|
$
\alpha = 1 - {\left[ {\left( {p - 1} \right){k_2}t + 1} \right]^{\frac{1}{{1 - p}}}}
$
|
(139) |
对方程(25-6), 由
|
$
\int_0^\alpha {\frac{1}{{{k_2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \int_0^t {{\rm{d}}t}
$
|
(140) |
知
|
$
\begin{array}{l}
\int_0^\alpha {\frac{1}{{{k_2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } = \frac{1}{{{k_2}}}\int_0^\alpha {\frac{1}{{1 - \alpha }}{\rm{d}}\alpha } = \frac{1}{{{k_2}}}\left[ { - \ln \left( {1 - \alpha } \right)} \right]\left| {_0^\alpha } \right.\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \frac{1}{{{k_2}}}\ln \left( {1 - \alpha } \right)
\end{array}
$
|
(141) |
得
|
$
- \frac{1}{{{k_2}}}\ln \left( {1 - \alpha } \right) = t
$
|
(142) |
|
$
\ln \left( {1 - \alpha } \right) = - {k_2}t
$
|
(143) |
|
$
\alpha = 1 - {{\rm{e}}^{ - {k_2}t}}
$
|
(144) |
2.5 自催化反应的α随T变化方程的导出途径
对第Ⅰ类动力学方程[11]
|
$
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{A}{\beta }\int_0^T {\exp \left( { - \frac{E}{{RT}}} \right){\rm{d}}T}
$
|
(145) |
由Frank-Kameneskii近似式[10]
|
$
\int_0^T {\exp \left( { - \frac{E}{{RT}}} \right){\rm{d}}T} = \frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(146) |
知
|
$
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(147) |
由第三类微分方程式(25-2), 知
|
$
f\left( \alpha \right) = {\left( {\alpha + {\alpha _0}} \right)^2}\left( {1 - \alpha } \right)
$
|
(148) |
|
$
\begin{array}{l}
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} \\
= \int_0^\alpha {\frac{1}{{{{\left( {\alpha + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \int_0^\alpha {\frac{{{{\left( {1 + {\alpha _0}} \right)}^2}}}{{{{\left( {1 + {\alpha _0}} \right)}^2}{{\left( {\alpha + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \int_0^\alpha {\left[ {\frac{1}{{\left( {1 + {\alpha _0}} \right){{\left( {\alpha + {\alpha _0}} \right)}^2}}} + \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}} + \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}\left( {\alpha + {\alpha _0}} \right)}}} \right]{\rm{d}}\alpha } \\
= \left[ { - \frac{1}{{\left( {1 + {\alpha _0}} \right)\left( {\alpha + {\alpha _0}} \right)}} - \frac{{\ln \left( {1 - \alpha } \right)}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}} + \frac{{\ln \left( {\alpha + {\alpha _0}} \right)}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}} \right]\left| {_0^\alpha } \right.\\
= - \frac{1}{{\left( {1 + {\alpha _0}} \right)\left( {\alpha + {\alpha _0}} \right)}} - \frac{{\ln \left( {1 - \alpha } \right)}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}} + \frac{{\ln \left( {\alpha + {\alpha _0}} \right)}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}} + \\
\;\;\frac{1}{{\left( {1 + {\alpha _0}} \right){\alpha _0}}} - \frac{{\ln {\alpha _0}}}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\\
= \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{\left( {1 + {\alpha _0}} \right){\alpha _0}}} - \frac{1}{{\left( {1 + {\alpha _0}} \right)\left( {\alpha + {\alpha _0}} \right)}}\\
= \frac{1}{{1 + {\alpha _0}}}\left[ {\frac{1}{{1 + {\alpha _0}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right]
\end{array}
$
|
(149) |
由式(147)和式(149)联立, 得
|
$
\frac{1}{{1 + {\alpha _0}}}\left[ {\frac{1}{{1 + {\alpha _0}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right] = \frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(150) |
由第二类微分方程式方程(25-3), 知
|
$
f\left( \alpha \right) = \left( {\alpha + {\alpha _0}} \right){\left( {1 - \alpha } \right)^2}
$
|
(151) |
|
$
\begin{array}{l}
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} \\
= \int_0^\alpha {\frac{1}{{\left( {\alpha + {\alpha _0}} \right){{\left( {1 - \alpha } \right)}^2}}}{\rm{d}}\alpha } \\
= \int_0^\alpha {\left[ {\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}\left( {1 - \alpha } \right)}} + \frac{1}{{\left( {1 + {\alpha _0}} \right){{\left( {1 - \alpha } \right)}^2}}} + \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}\left( {\alpha + {\alpha _0}} \right)}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\int_0^\alpha {\left[ {\frac{1}{{1 - \alpha }} + \frac{{1 + {\alpha _0}}}{{{{\left( {1 - \alpha } \right)}^2}}} + \frac{1}{{\alpha + {\alpha _0}}}} \right]{\rm{d}}\alpha } \\
= \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ { - \ln \left( {1 - \alpha } \right) + \frac{{1 + {\alpha _0}}}{{1 - \alpha }} + \ln \left( {\alpha + {\alpha _0}} \right)} \right]\left| {_0^\alpha } \right.\\
= \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ { - \ln \left( {1 - \alpha } \right) + \frac{{1 + {\alpha _0}}}{{1 - \alpha }} + \ln \left( {\alpha + {\alpha _0}} \right) - \left( {1 + {\alpha _0}} \right) - \ln {\alpha _0}} \right]\\
= \frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{\alpha \left( {1 + {\alpha _0}} \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right]
\end{array}
$
|
(152) |
由式(147)和式(152)联立, 得
|
$
\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{\alpha \left( {1 + {\alpha _0}} \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right] = \frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(153) |
由第一类微分方程式方程(25-4), 知
|
$
f\left( \alpha \right) = \left( {\alpha + {\alpha _0}} \right)\left( {1 - \alpha } \right)
$
|
(154) |
|
$
\begin{array}{l}
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} \\
= \int_0^\alpha {\frac{1}{{\left( {\alpha + {\alpha _0}} \right)\left( {1 - \alpha } \right)}}{\rm{d}}\alpha } \\
= \frac{1}{{{\alpha _0} + 1}}\int_0^\alpha {\left( {\frac{1}{{\alpha + {\alpha _0}}} + \frac{1}{{1 - \alpha }}} \right){\rm{d}}\alpha } \\
= \frac{1}{{{\alpha _0} + 1}}\left[ {\ln \left( {\alpha + {\alpha _0}} \right) - \ln \left( {1 - {\alpha _0}} \right)} \right]\left| {_0^\alpha } \right.\\
= \frac{1}{{{\alpha _0} + 1}}\left[ {\ln \left( {\alpha + {\alpha _0}} \right) - \ln \left( {1 - {\alpha _0}} \right) - \ln {\alpha _0}} \right]\\
= \frac{1}{{{\alpha _0} + 1}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}
\end{array}
$
|
(155) |
由式(147)和式(155)联立, 得
|
$
\frac{1}{{{\alpha _0} + 1}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(156) |
|
$
\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)
$
|
(157) |
|
$
\alpha + {\alpha _0} = {\alpha _0}\left( {1 - \alpha } \right)\exp \left[ {\frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right]
$
|
(158) |
|
$
\begin{array}{l}
\left\{ {1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right]} \right\}\alpha \\
= {\alpha _0}\left\{ {\exp \left[ {\frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}
\end{array}
$
|
(159) |
|
$
\begin{array}{l}
\alpha = \frac{{{\alpha _0}\left\{ {\exp \left[ {\frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right]}}\\
\;\;\; = 1 - \frac{{1 + {\alpha _0}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\frac{{R{T^2}}}{E}\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right]}}
\end{array}
$
|
(160) |
对第Ⅱ类动力学方程[11]
|
$
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{A}{\beta }\int_{{T_0}}^T {\left[ {1 + \frac{E}{{RT}}\left( {1 - \frac{{{T_0}}}{T}} \right)} \right]\exp \left( { - \frac{E}{{RT}}} \right){\rm{d}}T}
$
|
(161) |
由
|
$
\int_{{T_0}}^T {\left[ {1 + \frac{E}{{RT}}\left( {1 - \frac{{{T_0}}}{T}} \right)} \right]\exp \left( { - \frac{E}{{RT}}} \right){\rm{d}}T} = \left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(162) |
知
|
$
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(163) |
由式(149)和(163)式联立, 得
|
$
\frac{1}{{1 + {\alpha _0}}}\left[ {\frac{1}{{1 + {\alpha _0}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right] = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(164) |
由式(152)和式(163)联立, 得
|
$
\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{{\alpha _0}\left( {1 - \alpha } \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right] = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(165) |
由式(155)和式(163)联立, 得
|
$
\frac{1}{{{\alpha _0} + 1}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)
$
|
(166) |
|
$
\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)
$
|
(167) |
|
$
\alpha + {\alpha _0} = {\alpha _0}\left( {1 - \alpha } \right)\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right]
$
|
(168) |
|
$
\begin{array}{l}
\left\{ {1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right]} \right\}\alpha \\
= {\alpha _0}\left\{ {\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}
\end{array}
$
|
(169) |
|
$
\begin{array}{l}
\alpha = \frac{{{\alpha _0}\left\{ {\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right]}}\\
\;\;\; = 1 - \frac{{1 + {\alpha _0}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( { - \frac{E}{{RT}}} \right)\left( {{\alpha _0} + 1} \right)} \right]}}
\end{array}
$
|
(170) |
由Harcourt-Esson方程的积分式(171)[12]
|
$
\begin{array}{l}
G\left( \alpha \right) = \int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{A}{\beta }\int_0^T {{T^a}{\rm{d}}T} \\
\;\;\;\;\;\;\;\;\; = \frac{{{A_0}}}{\beta }\frac{1}{{a + 1}}{T^{a + 1}}\left| {_0^T} \right. = \frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}
\end{array}
$
|
(171) |
与式(149)联立, 得
|
$
\frac{1}{{1 + {\alpha _0}}}\left[ {\frac{1}{{1 + {\alpha _0}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 + \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right] = \frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}
$
|
(172) |
由式(152)和式(171)联立, 得
|
$
\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{\alpha \left( {1 - {\alpha _0}} \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right] = \frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}
$
|
(173) |
由式(155)和式(171)联立, 得
|
$
\frac{1}{{{\alpha _0} + 1}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}
$
|
(174) |
|
$
\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}\left( {{\alpha _0} + 1} \right)
$
|
(175) |
|
$
\alpha + {\alpha _0} = {\alpha _0}\left( {1 - \alpha } \right)\exp \left[ {\frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}\left( {{\alpha _0} + 1} \right)} \right]
$
|
(176) |
|
$
\begin{array}{l}
\left\{ {1 + {\alpha _0}\exp \left[ {\frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}\left( {{\alpha _0} + 1} \right)} \right]} \right\}\alpha \\
= {\alpha _0}\left\{ {\exp \left[ {\frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}
\end{array}
$
|
(177) |
|
$
\begin{array}{l}
\alpha = \frac{{{\alpha _0}\left\{ {\exp \left[ {\frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}\left( {{\alpha _0} + 1} \right)} \right]}}\\
\;\;\; = 1 - \frac{{1 + {\alpha _0}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{{\beta \left( {a + 1} \right)}}{T^{a + 1}}\left( {{\alpha _0} + 1} \right)} \right]}}
\end{array}
$
|
(178) |
由Berthelot方程的积分式(179)[12]
|
$
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} \approx \frac{A}{{b\beta }}\exp \left( {bT} \right)
$
|
(179) |
与式(149)式联立, 得
|
$
\frac{1}{{1 + {\alpha _0}}}\left[ {\frac{1}{{1 + {\alpha _0}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right] = \frac{A}{{b\beta }}\exp \left( {bT} \right)
$
|
(180) |
由式(152)和式(179)联立, 得
|
$
\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{\alpha \left( {1 + {\alpha _0}} \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right] = \frac{A}{{b\beta }}\exp \left( {bT} \right)
$
|
(181) |
由式(155)和式(179)联立, 得
|
$
\frac{1}{{{\alpha _0} + 1}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{{b\beta }}\exp \left( {bT} \right)
$
|
(182) |
|
$
\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{{b\beta }}\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)
$
|
(183) |
|
$
\alpha + {\alpha _0} = {\alpha _0}\left( {1 - \alpha } \right)\exp \left[ {\frac{A}{{b\beta }}\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right]
$
|
(184) |
|
$
\begin{array}{l}
\left\{ {1 + {\alpha _0}\exp \left[ {\frac{A}{{b\beta }}\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right]} \right\}\alpha \\
= {\alpha _0}\left\{ {\exp \left[ {\frac{A}{{b\beta }}\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}
\end{array}
$
|
(185) |
|
$
\begin{array}{l}
\alpha = \frac{{{\alpha _0}\left\{ {\exp \left[ {\frac{A}{{b\beta }}\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{{b\beta }}\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right]}}\\
\;\;\; = 1 - \frac{{1 + {\alpha _0}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{{b\beta }}\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right]}}
\end{array}
$
|
(186) |
由积分式(187)[11]
|
$
\begin{array}{l}
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{A}{\beta }\int_0^T {\exp \left( {bT} \right)\left[ {1 + \left( {T - {T_0}} \right)b} \right]{\rm{d}}T} \\
\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)
\end{array}
$
|
(187) |
与式(149)联立, 得
|
$
\frac{1}{{1 + {\alpha _0}}}\left[ {\frac{1}{{1 + {\alpha _0}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right] = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)
$
|
(188) |
由式(152)和式(187)联立, 得
|
$
\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{\alpha \left( {1 + {\alpha _0}} \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right] = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)
$
|
(189) |
由式(155)和式(187)联立, 得
|
$
\frac{1}{{{\alpha _0} + 1}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)
$
|
(190) |
|
$
\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)
$
|
(191) |
|
$
\alpha + {\alpha _0} = {\alpha _0}\left( {1 - \alpha } \right)\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right]
$
|
(192) |
|
$
\begin{array}{l}
\left\{ {1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right]} \right\}\alpha \\
= {\alpha _0}\left\{ {\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}
\end{array}
$
|
(193) |
|
$
\begin{array}{l}
\alpha = \frac{{{\alpha _0}\left\{ {\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right]}}\\
\;\;\; = 1 - \frac{{1 + {\alpha _0}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }\left( {T - {T_0}} \right)\exp \left( {bT} \right)\left( {{\alpha _0} + 1} \right)} \right]}}
\end{array}
$
|
(194) |
由积分式(195)
|
$
\int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{A}{\beta }\int_0^T {{T^a}\left[ {1 + \left( {T - {T_0}} \right)\frac{a}{T}} \right]{\rm{d}}T} = \frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)
$
|
(195) |
与式(149)联立, 得
|
$
\frac{1}{{1 + {\alpha _0}}}\left[ {\frac{1}{{1 + {\alpha _0}}}\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} + \frac{1}{{{\alpha _0}}} - \frac{1}{{\alpha + {\alpha _0}}}} \right] = \frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)
$
|
(196) |
由式(152)和式(195)联立, 得
|
$
\frac{1}{{{{\left( {1 + {\alpha _0}} \right)}^2}}}\left[ {\frac{{\alpha \left( {1 + {\alpha _0}} \right)}}{{1 - \alpha }} + \ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}}} \right] = \frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)
$
|
(197) |
由式(155)和式(195)联立, 得
|
$
\ln \frac{{\alpha + {\alpha _0}}}{{{\alpha _0}\left( {1 - \alpha } \right)}} = \frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)\left( {{\alpha _0} + 1} \right)
$
|
(198) |
|
$
\alpha + {\alpha _0} = {\alpha _0}\left( {1 - \alpha } \right)\exp \left[ {\frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)\left( {{\alpha _0} + 1} \right)} \right]
$
|
(199) |
|
$
\begin{array}{l}
\left\{ {1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)\left( {{\alpha _0} + 1} \right)} \right]} \right\}\alpha \\
= {\alpha _0}\left\{ {\exp \left[ {\frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}
\end{array}
$
|
(200) |
|
$
\begin{array}{l}
\alpha = \frac{{{\alpha _0}\left\{ {\exp \left[ {\frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)\left( {{\alpha _0} + 1} \right)} \right] - 1} \right\}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)\left( {{\alpha _0} + 1} \right)} \right]}}\\
\;\;\; = 1 - \frac{{1 + {\alpha _0}}}{{1 + {\alpha _0}\exp \left[ {\frac{A}{\beta }{T^a}\left( {T - {T_0}} \right)\left( {{\alpha _0} + 1} \right)} \right]}}
\end{array}
$
|
(201) |
3 计算实例
由不同升温速率的DSC获得HNIW的试验数据见表 1。根据表 1中{(αi, Ti)}iN=1, 得ti=(Ti-T0)/β, i=1, 2, …, N及(dα/dt)i≈(αi-αi-1)/(ti-ti-1), i=1, 2, …, N。代数据: (dα/dt)i、αi, i=1, 2, …Li, 入自催化的n级反应(CnB)速率方程
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = A\exp \left( { - \frac{E}{{RT}}} \right){\left( {1 - \alpha } \right)^n}\left( {1 + {K_{{\rm{cat}}}}\alpha } \right)
$
|
(202) |
表 1(Tab. 1)

表 1 由DSC测得HNIW的数据[13]
Tab. 1 Data of HNIW determined by DSC[13]
| data point |
αi
|
Ti/K |
| 2 K·min-1 |
5 K·min-1 |
10 K·min-1 |
20 K·min-1 |
| 1 |
0 |
473.20 |
483.05 |
491.58 |
498.56 |
| 2 |
0.025 |
488.29 |
499.59 |
508.08 |
516.02 |
| 3 |
0.050 |
490.63 |
502.22 |
510.46 |
518.78 |
| 4 |
0.075 |
491.96 |
503.83 |
512.03 |
520.49 |
| 5 |
0.100 |
492.97 |
504.98 |
513.19 |
521.77 |
| 6 |
0.125 |
493.75 |
505.88 |
514.13 |
522.82 |
| 7 |
0.150 |
494.45 |
506.67 |
514.93 |
523.69 |
| 8 |
0.175 |
495.06 |
507.35 |
515.63 |
524.47 |
| 9 |
0.200 |
495.61 |
507.96 |
516.26 |
525.16 |
| 10 |
0.225 |
496.13 |
508.52 |
516.84 |
525.79 |
| 11 |
0.250 |
496.66 |
509.04 |
517.37 |
526.38 |
| 12 |
0.275 |
497.09 |
509.54 |
517.86 |
526.93 |
| 13 |
0.300 |
497.49 |
510.02 |
518.34 |
527.45 |
| 14 |
0.325 |
497.84 |
510.48 |
518.79 |
527.94 |
| 15 |
0.350 |
498.19 |
510.91 |
519.23 |
528.42 |
| 16 |
0.375 |
498.51 |
511.32 |
519.65 |
528.87 |
| 17 |
0.400 |
498.85 |
511.71 |
520.06 |
529.29 |
| 18 |
0.425 |
499.17 |
512.09 |
520.45 |
529.70 |
| 19 |
0.450 |
499.50 |
512.46 |
520.84 |
530.10 |
| 20 |
0.475 |
499.82 |
512.83 |
521.22 |
530.48 |
| 21 |
0.500 |
500.14 |
513.19 |
521.59 |
530.85 |
| 22 |
0.525 |
500.43 |
513.53 |
521.95 |
531.20 |
| 23 |
0.550 |
500.71 |
513.88 |
522.31 |
531.56 |
| 24 |
0.575 |
501.00 |
514.20 |
522.65 |
531.89 |
| 25 |
0.600 |
501.29 |
514.53 |
522.99 |
532.23 |
| 26 |
0.625 |
501.59 |
514.86 |
523.31 |
532.55 |
| 27 |
0.650 |
501.88 |
515.17 |
523.64 |
532.87 |
| 28 |
0.675 |
502.14 |
515.48 |
523.94 |
533.17 |
| 29 |
0.700 |
502.42 |
515.78 |
524.25 |
533.47 |
|
表 1 由DSC测得HNIW的数据[13]
Tab.1 Data of HNIW determined by DSC[13] |
的非线性优化模型
|
$
\mathop {\min }\limits_{A,E,n,{K_{{\rm{cat}}}}} \sum\limits_{i = 2}^N {{{\left[ {{{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)}_i} - A\exp \left( { - \frac{E}{{R{T_i}}}} \right){{\left( {1 - {\alpha _i}} \right)}^n}\left( {1 + {K_{{\rm{cat}}}}{\alpha _i}} \right)} \right]}^2}}
$
|
(203) |
s.t. 1012.5 s-1≤A≤1013.5 s-1, 150000 J·mol-1≤E≤165000 J·mol-1, 0.9≤n≤1.1, 10≤Kcat≤15
由线性最小二乘法和信赖域方法[4-6, 8]得模型中的4参数(A、E、n、Kcat)。
β=2 K·min-1时, 自催化分解反应的动力学参数为: E=160.46 kJ·mol-1, A=1013.52, Kcat=15.0, n=0.90;计算值与实验值的相对误差$\Delta \delta = \sqrt {\sum\limits_{i = 1}^n {{{[{{\left({{\rm{d}}\alpha {\rm{/d}}\mathit{t}} \right)}_{{\rm{cald}}, \mathit{i}}}-{{\left({{\rm{d}}\alpha {\rm{/d}}\mathit{t}} \right)}_{\exp, i}}]}^2}} /\sum\limits_{i = 1}^n { -\left({{\rm{d}}\alpha {\rm{/d}}\mathit{t}} \right)_{\exp, i}^2} } = 0.08814$; β=5 K·min-1时, 自催化分解反应动力学参数为: E=161.00 kJ·mol-1, A=1013.50, Kcat=15.0, n=0.90, Δδ=0.07289; β=10 K·min-1时, 自催化分解反应动力学参数为: E=158.77 kJ·mol-1, A=1013.30, Kcat=15.0, n=0.90, Δδ=0.07466; β=20 K·min-1时, 自催化分解反应动力学参数为: E=160.69 kJ·mol-1, A=1013.50, Kcat=15.0, n=0.90, Δδ=0.09100。
从计算结果可知, Δδ很小, 表明非等温条件下, 用CnB速率方程
|
$
{\rm{d}}\alpha /{\rm{d}}t = {10^{13.46}}\exp \left( { - 160230/RT} \right){\left( {1 - \alpha } \right)^{0.90}}\left( {1 + 15\alpha } \right)
$
|
描述HNIW的热分解过程是可取的。若视n=0.90≈1, 则可用方程(94)和(102)描述α随t的变化。
类似地, 由描述NC(12.82% N)自催化分解反应的速率方程[3]
|
$
\begin{array}{l}
{\rm{d}}\alpha /{\rm{d}}t = {10^{16.4}}\exp \left( { - 178000/RT} \right)\left( {1 - \alpha } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{17.0}}\exp \left( { - 174000/RT} \right)\alpha \left( {1 - \alpha } \right)
\end{array}
$
|
可得: Tmax=479.55 K, αmax=0.4539, Kcat=10.86。
由描述NC(12.97% N)自催化分解反应的速率方程[5]
|
$
\begin{array}{l}
{\rm{d}}\alpha /{\rm{d}}t = {10^{16.00}}\exp \left( { - 174520/RT} \right)\left( {1 - \alpha } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{16.00}}\exp \left( { - 163510/RT} \right)\alpha \left( {1 - \alpha } \right)
\end{array}
$
|
可得: Tmax=481.19 K, αmax=0.4680, Kcat=15.68。
由描述NC(13.54% N)自催化分解反应的速率方程[4]
|
$
\begin{array}{l}
{\rm{d}}\alpha /{\rm{d}}t = {10^{15.82}}\exp \left( { - 170020/RT} \right){\left( {1 - \alpha } \right)^{1.11}} + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{15.82}}\exp \left( { - 157140/RT} \right){\alpha ^{1.51}}{\left( {1 - \alpha } \right)^{2.51}}
\end{array}
$
|
可得: Tmax=482.25 K, αmax=0.3411, Kcat=24.84。
由描述NC(13.61% N)自催化分解反应的速率方程[3]
|
$
\begin{array}{l}
{\rm{d}}\alpha /{\rm{d}}t = {10^{16.5}}\exp \left( { - 184700/RT} \right)\left( {1 - \alpha } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{16.9}}\exp \left( { - 174700/RT} \right)\alpha \left( {1 - \alpha } \right)
\end{array}
$
|
可得: Tmax=478.75 K, αmax=0.4838, Kcat=30.98。
由描述NC(13.86% N)自催化分解反应的速率方程[14]
|
$
\begin{array}{l}
{\rm{d}}\alpha /{\rm{d}}t = {10^{16.30}}\exp \left( { - 181860/RT} \right)\left( {1 - \alpha } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{16.70}}\exp \left( { - 173050/RT} \right)\alpha \left( {1 - \alpha } \right)
\end{array}
$
|
可得: Tmax=477.00 K, αmax=0.4783, Kcat=23.16。
由描述NC(13.88% N)自催化分解反应的速率方程[3]
|
$
\begin{array}{l}
{\rm{d}}\alpha /{\rm{d}}t = {10^{16.40}}\exp \left( { - 181860/RT} \right)\left( {1 - \alpha } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{16.70}}\exp \left( { - 171730/RT} \right)\alpha \left( {1 - \alpha } \right)
\end{array}
$
|
可得: Tmax=476.95 K, αmax=0.4805, Kcat=25.67。
由描述NC(14.14% N)自催化分解反应的速率方程[6]
|
$
\begin{array}{l}
{\rm{d}}\alpha /{\rm{d}}t = {10^{15.76}}\exp \left( { - 170800/RT} \right){\left( {1 - \alpha } \right)^{0.95}} + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{15.76}}\exp \left( { - 159100/RT} \right){\alpha ^{1.81}}{\left( {1 - \alpha } \right)^{1.16}}
\end{array}
$
|
可得: Tmax=489.61 K, αmax=0.5756, Kcat=17.71。
上述计算结果表明, 非等温条件下, NC(13.54%、14.14% N)的热分解过程可用经验级数自催化反应速率方程(25)描述。NC(12.82%、12.97%、13.61%、13.86%、13.88% N)的热分解过程可用一级(m=1、n=1、p=1)自催化分解反应速率方程(25-13)描述。对一级自催化分解反应, 可用方程(56)和(59)描述αmax和Kcat的关系, 可用方程(57)和(58)描述(dα/dt)max和αmax、Kcat、E1/RTmax的关系, 可用方程(70)和(77)描述α随的t变化。E2大于E1, 表明:催化分解反应速率大于催化剂生成反应速率, 催化产物存在下的催化分解反应易于发生。
4 结论
(1) 导出了经验级数自催化反应速率方程和13个派生式。提出了描述自催化分解反应速率曲线特性的方程, 以及反应进度随时间和温度变化的方程。
(2) 描述HNIW分解过程的速率方程为自催化的n级反应(CnB)速率方程:
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = 1013.46\exp \left( { - \frac{{160230}}{{RT}}} \right){\left( {1 - \alpha } \right)^{0.90}}\left( {1 + 15\alpha } \right)
$
|
(3) 提出了正文中描述NC(12.82%、12.97%、13.54%、13.61%、13.86%、13.88%、14.14% N)自催化分解过程的反应动力学参数—催化系数Kcat、速率曲线特性参数和α随t变化的方程。
The kinetic parameters, rate curve characteristic parameters and the equation of change in reaction extent with time for the autocatalytic decomposition reaction of hexanitrohexaazaisowurtzitane (HNIW) and nitrocellulose (NC)(12.82%, 12.97%, 13.54%, 13.61%, 13.88%, 14.14% N) and the derived ways of equations used in calculation of these parameters were reported.