拔销器是利用电能使装填的烟火药爆燃, 产生高温高压气体推动活塞运动的装置, 该类装置已广泛用于航天系统[1]。拔销器主要由管壳、活塞、剪切销、电爆管、密封件等组成, 具有体积小、重量轻、所需激发能量小、使用安全、作用可靠、能够简化总体结构设计等特点。随着航天器越来越复杂, 拔销器的使用数量也越来越多, 可靠性要求也越来越高。在载人飞行中, 一般对拔销器的可靠度要求为0.999999(置信度0.95)[2]。目前针对该类产品的可靠性设计, 王鹏[3]、杜志明[4]等提到工程中一般采用冗余或裕度设计来保证产品的可靠度, 另外通过数值仿真[5]也可以对可靠性设计起到辅助作用, 但这些方法对产品的设计可靠度缺乏定量认识, 设计裕度过低不能保证产品的可靠性, 过高则浪费资源, 因此如何在设计阶段就能对产品的可靠度有定量认识就成为研究的难点。董海平[6]、沈超[7]等对火工品可靠性设计理论进行了相关研究, 可以借鉴用于拔销器的可靠性设计。
本研究以某拔销器为例, 首先对其功能和主要结构进行了介绍, 然后采用NESSUS软件对其进行可靠性设计与分析, 获得设计可靠度值, 并对影响其可靠度的参数进行敏感度和重要度分析, 为同类型产品的可靠性设计与优化提供参考。
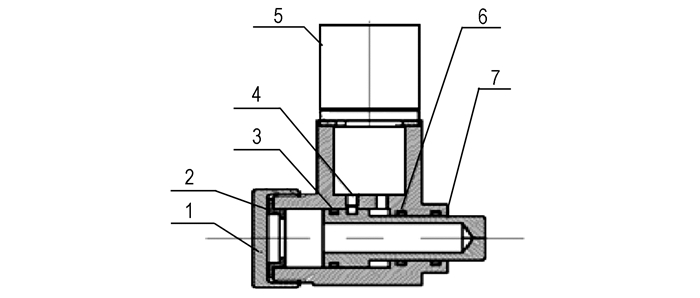
2 拔销器主要结构所研究的某拔销器结构简图如图 1所示。该拔销器的工作过程为电起爆器通电发火, 燃烧后产生的高温高压气体通过壳体传火孔进入组合件密封壳体腔内, 气体压力作用在活塞上, 使剪切销被剪切断, 活塞沿轴线方向回缩, 完成释放功能。
|
图 1 拔销器结构简图 1—螺盖, 2—缓冲环, 3—密封圈Ⅱ, 4—剪切销, 5—起爆器, 6—密封圈Ⅰ, 7—活塞 Fig.1 Structure diagram of retracting actuator 1—blind nut, 2—buffering ring, 3—seal ringⅡ, 4—shear pin, 5—initiator, 6—seal ringⅠ, 7—piston |
NESSUS(Numerical Evaluation of Stochastic Structures Under Stress)是一款用于系统概率分析的模块化计算软件, 最初是由SwRI(美国西南研究院)的力学与材料学部专门为NASA开发的, 用于航天飞机主发动机零件的失效概率分析、定量的可靠性预计和风险评估。后来, 美国西南研究院持续改进NESSUS并将其应用于更多领域的问题。NESSUS将世界上最新的概率算法与通用数值分析方法相结合, 计算工程系统的概率响应和可靠性, 定量评估零件、系统的可靠性, 识别重要随机变量, 为基于风险的决策分析和基于可靠性的优化设计提供信息, 开发比传统确定性设计方法更经济、更有效、更可靠的设计。NESSUS功能广泛, 并具有图形化用户界面, 并经过很多工程项目的验证。同时, NESSUS具有与多种目前流行的第三方和商业确定性分析软件的接口, 包括有限元软件(ABAQUS、ANSYS、MSC Nastran、LS-DYNA等)和多体动力学分析软件。
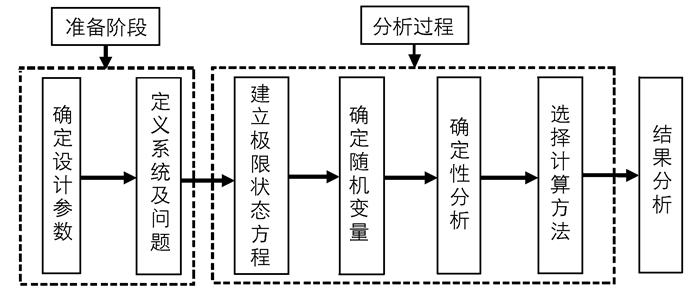
3.2 NESSUS分析流程应用NESSUS软件进行可靠性分析的流程如图 2所示。根据图 1所示的拔销器结构, 按照图 2所示的流程对其进行可靠性分析。在图 2所示步骤的第一步中设计结构及参数根据工程经验确定。
|
图 2 NESSUS可靠性分析流程 Fig.2 Reliability analysis process of NESSUS |
该步骤中系统指研究的对象, 问题指研究对象的失效状态。该软件可以同时定义研究对象的多种失效状态, 且可以利用故障树的逻辑符号来表示失效状态的逻辑关系。对于本研究的对象拔销器而言, 只有一种失效状态, 即若起爆器作用后的输出压力不足以克服剪切销的剪切力和密封圈的摩擦阻力, 则认为该结构作用失效。
3.2.2 建立极限状态方程该步骤主要是指将失效状态通过量化的形式表示出来。该软件的理论依据是应力-强度[8]干涉理论, 用极限状态函数g来表示应力与强度的差值, 当两者的差值小于0时, 系统就是可靠的。该部分的主要工作就是将该系统对应的“应力”和“强度”的表达式写出来。根据拔销器的作用过程及失效判据, g函数的定义如式(1)所示。
| $ g = 1.2({F_{\rm{M}}} + {F_{\rm{J}}}) - {F_{\rm{S}}} $ | (1) |
式中,FM为密封圈的摩擦力, N; FJ为剪切销的剪切力, N; FS为起爆器输出装药的输出压力, N。在分析时要涉及到具体的设计参数, 下面分别对FM,FJ,FS进行计算。
(1) 密封圈摩擦力FM的计算
设密封圈的摩擦力为F[9], 计算公式如式(2)所示。
| $ F = \frac{{0.19{\pi ^2}{\mu _{\rm{m}}}e{E_{\rm{m}}}{D_{\rm{m}}}{d_{\rm{m}}}}}{{1 - {\mu ^2}}} $ | (2) |
式中,μm为密封圈与外筒内壁之间的摩擦系数; Em为密封圈材料的弹性模量, Pa; Dm为密封圈外径, m; dm为圆截面直径, m; μ为密封圈材料的泊桑系数; e为预压缩率, e=(dm-bm)/dm, bm为沟槽底部至外筒内壁的距离, m。
本产品共有3个O型密封圈, 材料均为橡胶EP470, 密封圈与外筒内壁之间的摩擦系数μm=0.4, 弹性模量Em=7.84 MPa, 泊桑系数μ=0.47。其中一个为Ⅰ型标准密封圈, 设该型密封圈对应的摩擦力为FM1; 另两个为Ⅱ型标准密封圈, 设该型密封圈对应的摩擦力为FM2。这两型密封圈对应的外径、圆截面直径、沟槽底部与外筒内壁的距离不同。则密封圈对应的总的摩擦力FM如式(3)所示。
| $ {F_{\rm{M}}} = {F_{{\rm{M}}1}} + 2{F_{{\rm{M}}2}} $ | (3) |
式中,FM1为Ⅰ型密封圈对应的摩擦力,N; FM2为Ⅱ型密封圈对应的摩擦力,N。FM1,FM2按照公式(2)计算。
(2) 剪切销剪切力FJ[10]的计算
剪切力FJ可以按照工程中常用方法进行计算。计算公式如式(4)所示。
| $ {F_{\rm{J}}} = \frac{{\pi {d^2}}}{4} \times {\tau _{\rm{b}}} $ | (4) |
式中,d为销子的直径,m; τb=0.8σb, σb为材料拉伸强度极限,Pa。
(3) 起爆器输出压力FS的计算
对于密闭膛内高温高压燃气, 在压力不太高的情况, 一般认为p<600 MPa时, 则压力pm[10]可以按式(5)计算。
| $ {p_{\rm{m}}} = \frac{{f\rho }}{{1 - \alpha \rho }} $ | (5) |
式中,f为起爆器输出装药的火药力,J·kg-1;ρ为装填密度,kg·m-3;α为余容,m3·kg-1。其中余容α和密度ρ的关系用经验公式(6)表示[11]。
| $ \alpha \left( \rho \right) = {e^{ - 0.4\rho }} $ | (6) |
则该起爆器的输出压力可以按照式(7)来计算。
| $ {F_{\rm{S}}} = {p_{\rm{m}}}S $ | (7) |
式中,S为输出压力作用在活塞上的面积, m2。
根据以上各个参数的分析, 将g函数表示出来, 即最终建立的极限值状态方程如式(8)所示。
| $ \left\{ \begin{array}{l} g = 1.2({F_{\rm{M}}} + {F_{\rm{J}}}) - {F_{\rm{s}}}, {F_{\rm{M}}} = {F_{{\rm{M}}1}} + 2{F_{{\rm{M}}2}}\\ {F_1} = \frac{{0.19{\pi ^2}{\mu _{\rm{m}}}{e_1}{E_{\rm{m}}}{D_{{\rm{m1}}}}{d_{{\rm{m1}}}}}}{{1 - {\mu ^2}}}\\ {F_2} = \frac{{0.19{\pi ^2}{\mu _{\rm{m}}}{e_2}{E_{\rm{m}}}{D_{{\rm{m2}}}}{d_{{\rm{m2}}}}}}{{1 - {\mu ^2}}}\\ {e_1} = \left( {{d_{{\rm{m}}1}} - {b_{{\rm{m}}1}}} \right)/{d_{{\rm{m}}1}}, {e_2} = \left( {{d_{{\rm{m}}2}} - {b_{{\rm{m}}2}}} \right)/{d_{{\rm{m}}2}}\\ {F_{\rm{J}}} = \frac{{\pi {d^2}}}{4} \times {\tau _{\rm{b}}}, {\tau _{\rm{b}}} = 0.8{\sigma _{\rm{b}}}\\ {F_S} = PS, P = \frac{{f\rho }}{{1 - \alpha \rho }}, \alpha = \exp ( - 0.4 \times \rho ) \end{array} \right. $ | (8) |
当原材料的加工和产品的加工工况稳定时, g函数中涉及到的参数应该都是定值, 但是实际中存在众多不确定因素, 导致这些参数不是定值, 而是在一定范围内波动。考虑加工工艺、制造公差、材料性能变化及随机因素的影响, 将极限状态方程中所列出的主要参数作为随机变量来处理。其中各参数的均值为实际设计或测量的参数, 而方差则是根据工程经验、加工精度及同类型产品的变差系数等作为参考来选取的, 从保守角度考虑, 方差一般取的值较大。各参数服从的分布类型和参数值如表 1所示, 均采用国际单位, 各参数表示的意义已在3.2.2节说明。
| 表 1 极限状态方程中各参数的输入值 Tab.1 parameter value of limit state equation |
确定性分析是可靠性评估和灵敏度分析的前提, 只有理论上不发生失效的结构才能进行分析。执行确定性分析, 结果为g=-0.230441, 表明使用以上设定的参数进行可靠性分析是可行的。
3.2.5 选择计算方法在对结构进行可靠性分析时, 采用的是结合改进均值设计验算点搜寻的基于曲面的自适应重要度抽样法(AMV-AIS), 在该方法中, 极限状态曲面会自适应调整, 直到在允许误差和给定置信度下, 概率积分收敛为止。计算可得该产品的可靠度为0.99999999986。根据文献[12], 收集了该产品中起爆器在2001~2009年间共9批次427发产品在高温、低温和常温条件下的压力测试数据值, 通过环境因子将高温和低温条件下的输出压力都转化为常温条件下的输出压力。为保守考虑, 取这些批次中输出压力均值最小的数值作为计算用数据, 通过计算可得最小输出压力均值为62.72, 标准差为6.92, 单位为MPa。该输出压力的作用面积为90.32 mm2, 则该条件下作用在活塞上的均值为5664.87 N, 标准差为625.01 N。通过计算可得输出压力需要克服摩擦力(110.88 N)和剪切力的(131.88 N)对应的可靠度为0.99999999999。计算值与试验值的相对误差为1.3E-10, 在工程允许范围内。
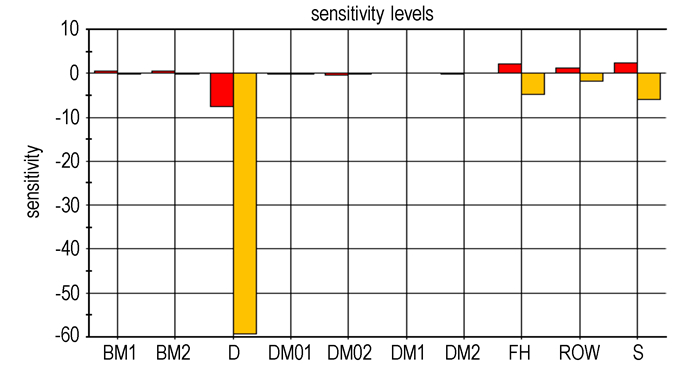
3.3 结果分析针对该结构, 灵敏度分析的结果如图 3所示。
|
图 3 关键参数灵敏度分析结果 Fig.3 Sensitivity analysis results of key parameter |
从图 3可以看出, 对该结构可靠度影响大的主要参数为剪切销直径(D)、起爆器输出装药的火药力(FH)、起爆器输出装药的密度(ROW)和输出压力的作用面积(S)。该产品的可靠度与剪切销直径成反比, 随着该设计值的减小, 输出可靠度增大, 与输出装药的火药力、输出装药的密度和输出压力的作用面积成正比, 随着这些值的增大, 可靠度增大; 密封圈的相关参数对可靠度相对影响较小。
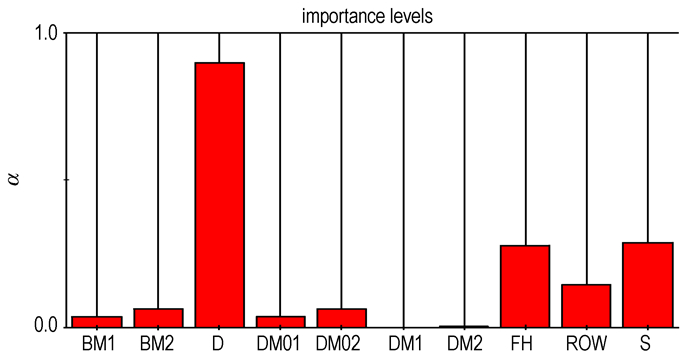
重要度分析结果如图 4所示。从图 4看出, 剪切销直径(D)、起爆器输出装药的火药力(FH)、输出装药的密度(ROW)和输出压力的作用面积(S)相对来说对可靠度影响较大, 其重要性程度顺序为:剪切销直径>起爆器输出压力的作用面积>输出装药的火药力>输出装药的密度。
|
图 4 关键参数重要度分析结果 Fig.4 Importance analysis results of key parameter |
(1) 在预定参数下产品的设计可靠度为0.99999999986, 与现场试验结果一致。
(2) 剪切销直径、起爆器输出压力的作用面积、输出装药的火药力和密度对产品可靠度影响较大, 可通过调节这些设计值的大小对产品的可靠性进行优化设计, 且在设计过程中应保持这些设计值的一致性。
| [1] |
王凯民, 温玉全.
军用火工品设计技术[M]. 北京: 国防工业出版社, 2006: 236-239.
WANG Kai-min, WEN Yu-quan. Design of initiators and pyrotechnics for weapon system[M]. Beijing: National Defense Industry Press, 2006: 236-239. |
| [2] |
李志强. 火工装置在航天飞行器上应用[J].
航天返回与遥感, 1997(2): 63-67. LI Zhi-qiang. The applications of pyrotechnics in spacecraft[J]. Spacecraft Recovery & Remote Sensing, 1997(2): 63-67. |
| [3] |
王鹏, 杜志明. 火工烟火装置裕度研究与设计方法综述[J].
火工品, 2005(2): 34-38. WANG Peng, DU Zhi-ming. Summarize of margin research and design method of pyrotechnic devices[J]. Initiators & Pyrotechnics, 2005(2): 34-38. |
| [4] |
杜志明, 范军政. 安全裕度研究与应用进展[J].
中国安全科学学报, 2004, 14(6): 6-10. DU Zhi-Ming, FAN Jun-Zheng. Progress in study and application of safety margin[J]. China Safety Science Journal, 2004, 14(6): 6-10. |
| [5] |
龙兵, 常新龙, 张磊, 等. 桥丝式电火工品发火过程的数值仿真[J].
火工品, 2009(5): 27-29. LONG Bing, CHANG Xin-long, ZHANG Lei, et al. Numerical simulation of firing sequence of bridge-wire EED[J]. Initiators & Pyrotechnics, 2009(5): 27-29. |
| [6] |
董海平, 蔡瑞娇, 穆慧娜, 等. 火工品可靠性的感度参数设计法[J].
爆炸与冲击, 2009, 29(6): 613-616. DONG Hai-ping, CAI Rui-jiao, Mu Hui-na, et al. The sensitivity parameters design method of initiators and pyrotechnics′reliability[J]. Explosion and Shock, 2009, 29(6): 613-616. |
| [7] |
沈超, 付丽璋, 吴世通, 等. 电容放电式火工品点火电路参数设计与仿真[J].
航天返回与遥感, 2011, 32(1): 63-73. SHEN Chao, Fu Li-zhang, Wu Shi-tong, et al. Ignition circuit parameters design and simulation of capacitor discharge initiators and pyrotechnics[J]. Aerospace Returning and Remote Sensing, 2011, 32(1): 63-73. |
| [8] |
王正, 谢里阳.
机械时变可靠性理论与方法[M]. 北京: 科学出版社, 2012: 47-77.
WANG Zheng, XIE Li-yang. Theory and methods mechanical time-varying reliability[M]. Beijing: Science Press, 2012: 47-77. |
| [9] |
徐辅仁. O形密封圈引起的摩擦力的计算[J].
润滑与密封, 1989(1): 32-34. XU Fu-ren. Calculating frictional force caused by O-ring seal[J]. Lubrication Engineering, 1989(1): 32-34. |
| [10] |
金忠谋.
材料力学[M]. 北京: 机械工业出版社, 2009: 64-65.
JIN Zhong-mou. Mechanics of materials[M]. Beijing: Machinery Industry Press, 2009: 64-65. |
| [11] |
金志明.
枪炮内弹道学[M]. 北京: 北京理工大学出版社, 2004: 188-189.
JIN Zhi-ming. The ballistics of interior guns[M]. Beijing: Beijing Institute of Technology, 2004: 188-189. |
| [12] |
赵霞. 某拔销器可靠性设计方法研究[D]. 北京: 北京理工大学, 2011.
ZHAO Xia. The research on some retracting actuator′s reliability design method[D]. Beijing: Beijing Institute of Technology, 2011. |

The reliability analysis for a retracting actuator was carried out by NESSUS software based on the stress-strength interference theory. The design reliability value was obtained. The sensitivity and importance analysis on random variables which affect the design reliability were done.



