2. 91049部队, 山东 青岛 266102
2. The 91049th Unit of PLA, Qingdao 266102, China
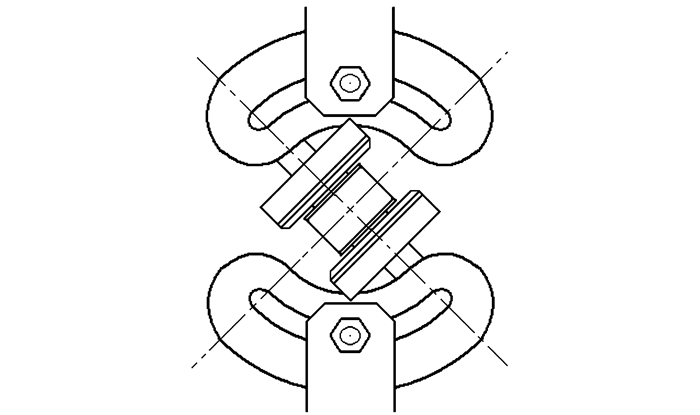
固体火箭发动机壳体/绝热层/衬层/推进剂各界面良好的粘接是保证发动机装药结构完整性的关键, 由于发动机头部、中部和尾部粘接系统所承受的载荷方向不同, 发动机在贮存、运输、吊装、点火工作时, 粘接系统各部位所承受的载荷方向也会发生变化, 导致粘接系统承受拉伸、剪切以及混合应力状态, 因此有必要测试粘接系统在各种受载状态下的力学性能。目前多采用单纯拉伸[1-2]、单纯剪切[3-4]以及剥离[5-6]的试验方法测试粘接系统的力学性能, 可经过耦合计算得到界面在拉伸、剪切混合载荷下的强度, 或者采用不区分拉伸、剪切应力的强度准则来衡量界面粘接强度。采用拉伸、剪切混合加载的试验方法, 可以避免拉伸剪切不同试件及其夹具的制作过程, 同时可以直接获得试件在混合载荷下的强度。国外曾经对固体火箭发动机壳体/绝热层/衬层/推进剂矩形粘接试件进行了多种角度的拉伸试验[7-8], 其夹具的拉伸角度采用无级调节方式, 如图 1所示, 但每次测试均要精确测量试件拉伸角度, 步骤繁琐。当试件受载变形后, 夹具无法控制试件的旋转自由度, 形成对试件剪切、剥离的混合加载状态, 不能实现纯剪切。
采用有限元计算结果, 获得试件界面的应力分布, 并结合试件的拉伸试验结果, 计算界面失效部位的粘接强度, 是目前最常用的分析方法。文献[9]给出了含人工脱粘层的矩形粘接试件应力分布的三维有限元法计算结果, 采用最大畸变能准则, 给出了在单纯拉伸状态下界面强度及其受绝热层模量变化的影响规律。文献[10-11]根据矩形试件的多角度拉伸试验结果, 发现采用最大主应力作为界面的强度准则, 其结果受试件拉伸角度的影响较小, 而采用最大拉应力、最大剪应力以及最大畸变能准则获得的界面强度受拉伸角度影响明显。
综合上述分析可知, 有必要设计一种能够测试标准试件在拉伸、剪切等各种混合载荷状态下力学性能的新型夹具, 使试件界面受载状态与发动机界面实际受载状态更为接近, 并结合有限元计算得到试件界面的应力分布, 获取界面失效部位的临界应力, 以提高试验效率和试验结果的准确程度。
本研究采用多角度拉伸与有限元计算相结合的方法, 考察了矩形粘接试件在拉伸、剪切混合载荷条件下的失效规律, 分析了试件拉伸角度对界面失效临界应力的影响。
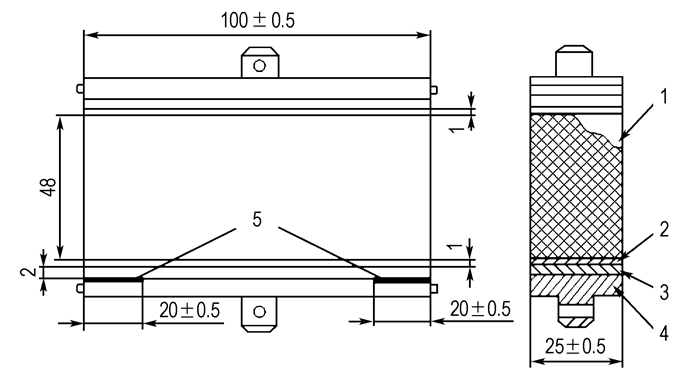
2 试验部分 2.1 夹具设计采用QJ 2038.1A-2004[2]所规定的矩形粘接试件进行试验, 其尺寸如图 2所示, 试件采用端羟基聚丁二烯(HTPB)推进剂、HTPB衬层以及丁腈橡胶绝热层, 为了模拟发动机人工脱粘结构, 并缓解试件界面边缘处的应力集中程度, 在绝热层与钢板之间有2处宽度为20 mm的人工脱粘层。
|
图 2 矩形粘接试件尺寸(单位: mm) 1—推进剂, 2—衬层, 3—绝热层, 4—钢板, 5—人工脱粘层 Fig.2 Size of rectangular adhesive specimen (unit: mm) 1—propellant, 2—liner, 3—insulator, 4—steel plate, 5—flap |
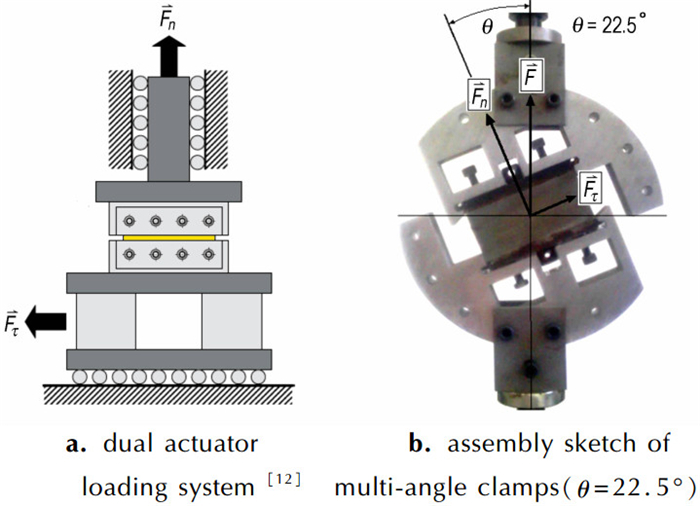
若对矩形粘接试件施加拉伸、剪切载荷, 目前通常的方法是利用双轴力学拉伸机对试件同时施加纵向和横向位移[12], 如图 3a所示。为了能够在单轴力学拉伸机上对试件同时施加拉伸、剪切载荷, 一种可行的方法是将纵向和横向位移矢量依据平行四边形法则合并为一个位移矢量, 则拉伸机测得的载荷F可分解为试件界面的法向拉伸载荷Fn和切向剪切载荷Fτ, 依此原理设计了一种可以旋转的夹具, 如图 3b所示, 图中拉伸机的拉伸方向与试件界面法线的夹角θ为拉伸角度, 本夹具设计了5个拉伸角度, 分别为0°、22.5°、45°、67.5°和90°, 每个拉伸角度所对应的拉伸载荷与剪切载荷大小可根据式(1)(2)计算。
| $ {F_n} = F \cdot {\rm{cos}}\theta $ | (1) |
| $ {F_\tau } = F \cdot {\rm{sin}}\theta $ | (2) |
|
图 3 实现混合载荷的两种方式 Fig.3 Two systems for mixed load |
若保证拉伸过程中试件所受的拉伸载荷与剪切载荷的合力始终为拉伸机的拉伸载荷, 需限制夹具的旋转自由度, 为此夹具设计时采用了如下结构及部件。
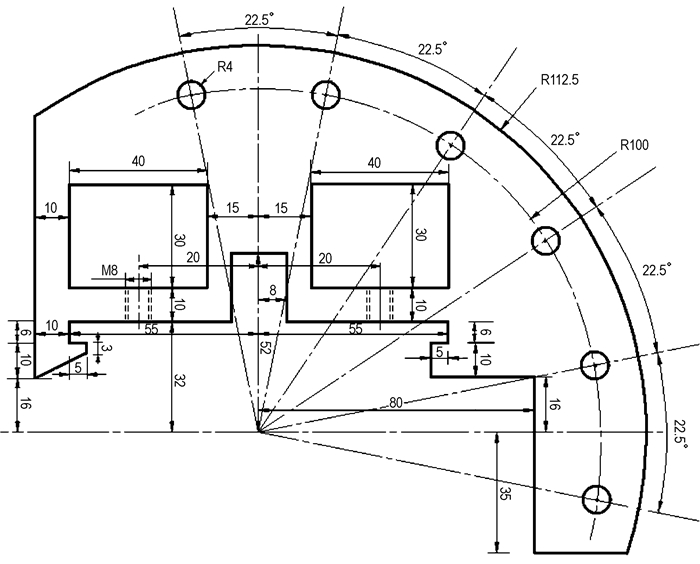
夹具分为两部分:一部分是与试件相连接的夹具盘, 其厚度为30 mm, 包含与试件金属部分相连接且凹凸配合的凹槽, 以及边缘用于安装销钉的6个圆形通孔, 其尺寸如图 4所示; 另一部分是连接三思公司CMT6203电子万能试验机夹头和夹具盘的适配接头部分, 其尺寸如图 5所示, 螺孔紧固圆板旋紧后可以使螺纹延伸杆与矩形连接片完全固定, 矩形连接片下方的2个通孔与夹具盘边缘任意相邻的2个通孔重合, 经销钉连接后二者可完全固定。
|
图 4 夹具盘的尺寸(单位: mm) Fig.4 Size of clamp plate (unit: mm) |

|
图 5 夹具适配接头尺寸 Fig.5 Size of clamp adapter |
与图 1所示夹具相比, 本研究设计的夹具有如下优点:由于夹具与拉伸机之间完全固定, 可以对试件进行纯剪切试验, 而非近似剪切试验; 在夹具加工精密并与拉伸机准确固定的条件下, 经测量拉伸角度误差控制在0.5°之内, 在对试验结果准确程度没有特别严格的要求时, 每次试验无需测量实际的拉伸角度, 从而提高试验效率。
2.2 试验过程首先, 将试件嵌入上、下夹具盘中, 并将4个矩形通孔内的螺栓拧紧以固定试件。选择所需的拉伸角度θ, 然后, 将4个矩形连接片通过螺栓固定在上、下夹具盘的两侧, 矩形连接片下部两个通孔与半圆形金属夹具盘边缘相邻两个通孔重合, 矩形连接片通过螺栓与半圆形金属夹具盘连接; 矩形连接片中部通孔与螺纹延伸杆上的通孔重合, 采用销钉连接; 紧固圆板的螺孔与延伸杆上的螺纹相配合, 紧固圆板穿过延伸杆, 并顶住与延伸杆相连的2个矩形连接片, 实现螺纹延伸杆与2个矩形连接片的固定。最后, 将装配好的夹具下延伸杆插入拉伸机下方静止夹头中, 并用销钉固定, 将拉伸机上方夹头降下, 并将夹具上延伸杆采用销钉固定。
为记录试件从拉伸变形至断裂的整个过程, 将数码照相机固定于三脚架上, 根据试件倾斜角度调节相机倾斜角, 并在相机视野中预留出试件变形后的空间, 当试件开始被拉伸时, 照相机以30 s的时间间隔开始连续拍摄, 为尽可能捕捉到试件界面起裂时刻的形貌, 采用了较低的拉伸速率(1 mm·min-1), 低于标准[2]规定的拉伸速率(20 mm·min-1), 对试件进行了不同拉伸角度的力学性能测试, 试件拉伸角度与对应载荷如表 1所示。
| 表 1 试件拉伸角度与对应载荷 Tab.1 Tensile angle and corresponding loading |
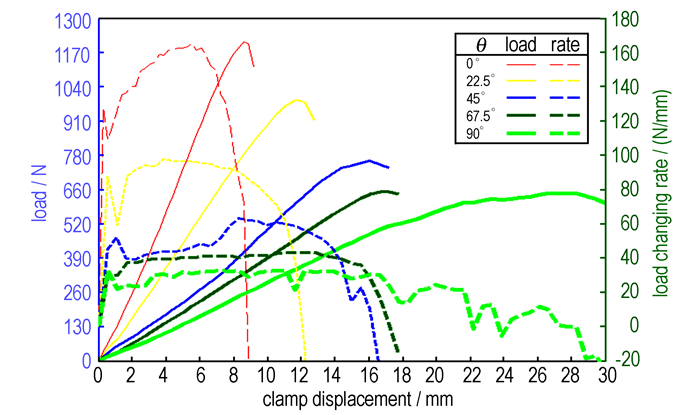
试件拉伸过程中,夹具载荷F及其变化速率dF/dL随夹具位移L的变化曲线如图 6所示。当拉伸角度从0°开始以22.5°为间隔逐渐增加时, 载荷位移曲线上升速率峰值呈逐渐下降的趋势, 由0°的160 N·mm-1降至22.5°的100 N·mm-1和45°的60 N·mm-1, 随后降速放缓, 分别降至67.5°的40 N·mm-1和90°的30 N·mm-1。
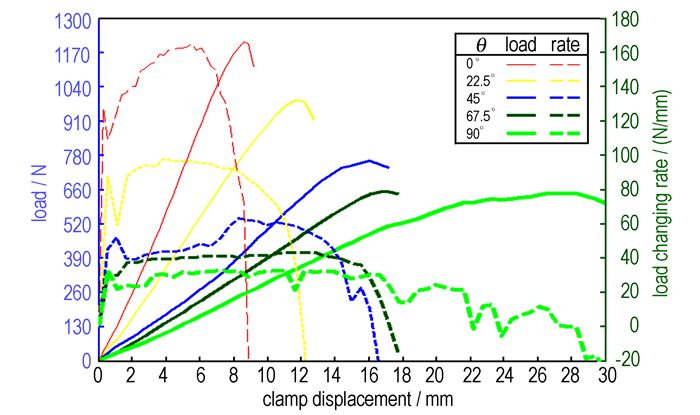
|
图 6 不同拉伸角度情况下载荷及其变化速率随夹具拉伸位移的变化曲线 Fig.6 Curves of clamp load (F) and its changing rate (dF/dL) vs. clamp displacement (L) with different tensile angle |
试件起裂载荷及其对应的夹具位移随拉伸角度的变化曲线如图 7所示。试件起裂载荷随着拉伸角度的增加而逐渐下降, 说明拉伸角度越大, 试件粘接界面越容易失效; 试件起裂时夹具的位移随着拉伸角度的增加呈现先上升后下降的过程。若要分析试件失效时的临界载荷及夹具位移出现上述变化规律的原因, 应当进一步分析试件的应力分布情况。
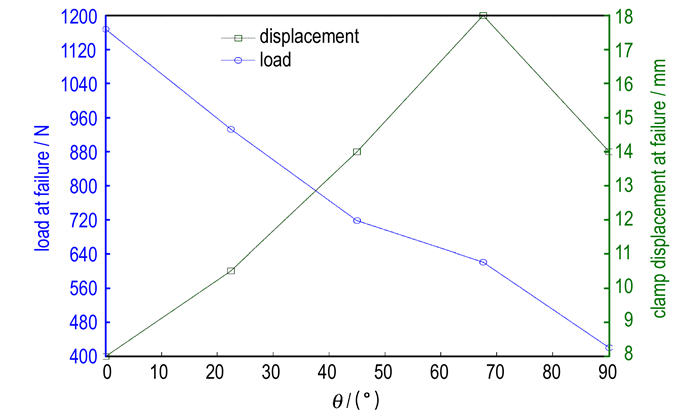
|
图 7 试件起裂载荷及其对应的夹具位移随拉伸角度的变化曲线 Fig.7 Curves of fracture initiation load and corresponding clamp displacement vs. tensile angle |
图 8给出了试件在拉伸过程中界面局部起始断裂临界时刻的外观形貌, 以及与其相对应的有限元数值模拟计算的外观形貌和最大主应力分布。文献[10]认为, 对于推进剂这种颗粒填充复合材料, 在受到剪切应力时, 填充的颗粒分布会重新组织, 从而将剪切应力转变为沿着最大主应力方向的拉伸应力。因此推进剂、衬层、绝热层粘接系统在受到不同方向的载荷后, 界面附近推进剂的局部变形会使之趋向于沿最大主应力方向拉伸的状态变化。而Mises应力即便在界面出现受压的状态时, 其数值仍与受拉状态相等, 这显然与实际相背, 因此采用了最大主应力进行分析。

|
图 8 不同拉伸角度条件下试件起裂时刻的变形形貌(左)与最大主应力的分布(右) Fig.8 Deformation of specimen from test(left) and maximum principal stress distribution from calculation(right)when fracture initiating with different tensile angles |
试件在各种拉伸角度下多为推进剂/衬层界面起裂, 因此在有限元计算结果中提取了该界面的应力, 仅有在拉伸角为67.5°时出现了衬层/绝热层界面起裂, 这可能由于试件制作工艺和材料性能的随机性所导致。为方便分析, 将试件人工脱粘层裂口尖端附近的推进剂、衬层、绝热层界面记为Flap位置, 该处起裂称为Flap型断裂; 将试件右上角无脱粘一侧边缘的推进剂、衬层、绝热层界面记为Edge位置, 该处起裂称为Edge型断裂, 如图 8所示。
由图 8中的最大主应力云图可知, 随着拉伸角θ的增加, 试件起裂时刻Flap位置的最大主应力逐渐下降, Edge位置的最大主应力呈逐渐上升的趋势。拉伸角θ为0°、22.5°、45°时, 试件起裂时刻Flap位置最大主应力明显高于其它区域, 试件为Flap型断裂; 拉伸角θ为67.5°时, 试件起裂时刻Flap位置与Edge位置最大主应力相近, Flap位置与Edge位置几乎同时裂; 拉伸角θ为90°时, 试件起裂时刻Edge位置最大主应力则明显高于其它区域, 为Edge型断裂。
3.2 界面失效准则分析通过有限元计算, 获得了不同拉伸角度下, 试件起裂时刻上侧和下侧推进剂、衬层界面最大主应力(σmp)θ的分布, 最大主应力集中系数(SRmp)θ的分布由(σmp)θ的分布除以最大主应力平均值(σmp)θ获得, 其结果如图 9、10所示。
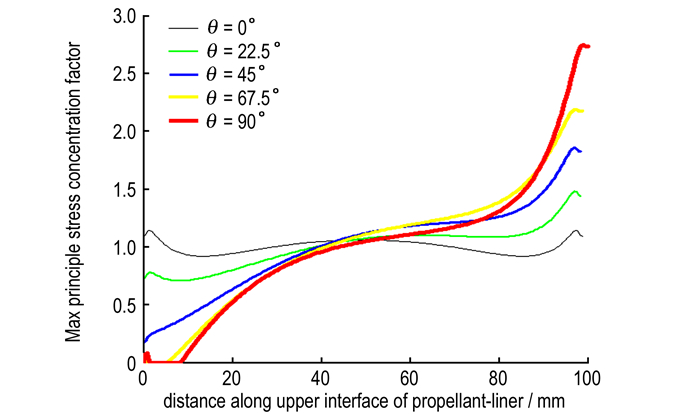
|
图 9 试件起裂时上侧推进剂/衬层界面(SRmp)θ的分布 Fig.9 Distribution of stress concentration factor (SRmp)θ along propellant/liner interface of the upper end tab when fracture initiating with different tensile angles |
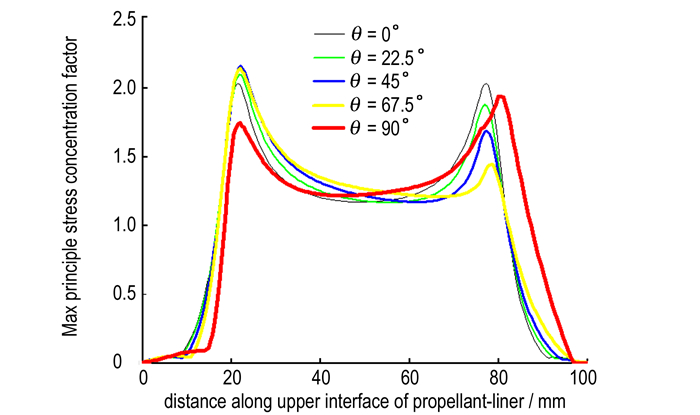
|
图 10 试件起裂时下侧推进剂/衬层界面(SRmp)θ的分布 Fig.10 Distribution of (SRmp)θ along propellant/liner interface of the lower end tab when fracture initiating |
在试件局部起裂时刻, 上界面Edge位置的应力集中系数(SRmp)θ由θ=0°时的1.1迅速上升至θ=90°时的2.7;下界面Flap位置的应力集中系数(SRmp)θ由θ=0°时的2.027缓慢增至θ=67.5°时的2.155, 然后迅速下降至θ=90°时的1.935。
界面失效部位起裂时最大主应力可根据式(3)计算。
| $ {\left( {{\sigma _{cr}}} \right)_\theta } = \frac{{{{\left( {{F_{cr}}} \right)}_\theta }}}{S}{\left( {S{R_{mp}}} \right)_\theta } $ | (3) |
式中, (σcr)θ为界面失效部位起裂时最大主应力, MPa; (Fcr)θ为试件界面起始失效时拉伸机载荷, N; θ为试件起裂部位的截面积, mm2; (SRmp)θ为失效位置的最大主应力应力集中系数。
试件裂纹萌生时刻力学性能的测量与计算值如表 2所示, 起裂位置与计算得到的起裂应力一致性较好, 尤其是试件拉伸角度为67.5°时, Flap位置与Edge位置的应力分别为0.530, 0.541 MPa, 相差仅2%左右, 而试验观察到的结果恰好为Flap位置与Edge位置几乎同时断裂, 从侧面证明该种计算分析方法的合理性。
| 表 2 试件裂纹萌生时刻力学性能的测量与计算值 Tab.2 Measured and calculated mechanical properties when fracture initiating |
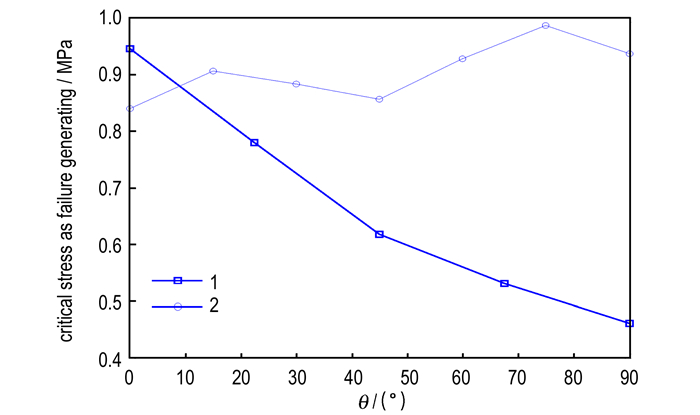
(σcr)θ随拉伸角度的变化曲线如图 11中曲线1所示, 随着θ由0°增至90°, (σcr)θ则由0.945 MPa逐渐降至0.461 MPa。而文献[10]采用了与本文结构相同的试件, 得到的(σcr)θ随θ变化幅度较小, 如图 11曲线2所示, 造成这种显著差别主要有两方面的原因:一是推进剂、衬层、绝热层配方和粘接工艺的不同; 二是采用的夹具构造上的差异, 文献[10]的夹具与图 1中夹具类似, 在拉伸过程中无法控制夹具旋转自由度, 形成了拉伸、剪切、剥离耦合加载形式, 缓解了剪切载荷对界面造成的损伤程度。若要证明上述猜测是否正确, 从细观的角度分析界面在不同载荷条件下的失效机理, 是一种可行的途径。
|
图 11 推进剂/衬层界面失效的临界最大主应力随拉伸角度θ的变化曲线 Fig.11 Curves of critical maximum principal stress vs. tensile angle when fracture initiating at propellant/liner interface |
(1) 设计的多角度拉伸夹具可以运用到矩形粘接试件的力学性能测试中, 试件在拉伸角度为0°, 22.5°, 45°时为Flap位置断裂, 90°时为Edge位置断裂, 67.5°时为Flap和Edge位置同时断裂。根据试件界面附近最大主应力集中系数的分布可以准确预测试件在不同拉伸角度下的断裂位置。
(2) 对于本研究所采用的矩形粘接试件, 随着拉伸角度由0°增至90°, 界面起裂时的最大主应力呈逐渐下降的趋势, 由0.945 MPa逐渐降至0.461 MPa。这种力学性能随载荷角度变化的规律可以应用到发动机粘接系统的结构完整性分析中, 以提高分析的精度。可以通过增加夹具盘的开孔数量, 以提供更多的拉伸角度选择, 提高结果的准确性。
| [1] |
QJ 2038. 1-1991, 固体火箭发动机燃烧室界面粘接强度测试方法-扯离法[S]. 1991.
|
| [2] |
QJ 2038. 1A-2004, 固体火箭发动机燃烧室界面粘接强度测试方法: 矩形试件扯离法[S]. 2004.
|
| [3] |
QJ 2038. 2-1991, 固体火箭发动机燃烧室界面粘接强度测试方法-剪切法[S]. 1991.
|
| [4] |
邢耀国, 金广文, 许学春, 等. 某型固体火箭发动机综合性能试验与寿命评估[J].
推进技术, 2004, 25(2): 176-179. XING Yao-guo, JIN Guang-wen, XU Xue-chun, et al. Comprehensive property tests and service life evaluation for solid rocket motors[J]. Journal of Propulsion Technology, 2004, 25(2): 176-179. |
| [5] |
何德伟, 刘戎, 侯少锋. 一种单室双推力发动机装药Ⅱ界面粘接性能研究[J].
上海航天, 2012, 29(2): 69-72. HE De-wei, LIU Rong, HOU Shao-feng. Factors of influencing bound characteristics at Ⅱ Interface of a single chamber dual thrust solid rocket motor grains[J]. Aerospace Shanghai, 2012, 29(2): 69-72. |
| [6] |
Haska S B, Bayramli E, Pekel F, et al. Adhesion of an HTPB-IPDI-based liner elastomer to composite matrix and metal case[J].
Journal of Applied Polymer Science, 1997, 64(12): 2355-2362. DOI:10.1002/(ISSN)1097-4628 |
| [7] |
Christiansen A G, Laheru K L, Anderson G P. Cohesive and adhesive analog test specimens for solid propellant grain simulation[R]. AIAA-1983-1118. 1983.
|
| [8] |
Anderson J M, Pavelka T D, Bruno P S. Techniques for assessing case liner-bond integrity in solid propellant rocket motors[R]. AD-768315, 1973.
|
| [9] |
王至存, 朱祖念, 张善祁. 固体发动机药柱粘结试件的三维应力分析[J].
宇航学报, 1996, 17(4): 34-38. WANG Zhi-cun, ZHU Zu-nian, ZHANG Shan-qi. The three dimensional stress analysis of solid motor grain's analog bond specimen[J]. Journal of Astronautics, 1996, 17(4): 34-38. |
| [10] |
Kuhlmann T L, Peeters R L, Bills K W. Modified maximum principal stress criterion for propellant liner bond failures[J].
Journal of Propulsion, 1987, 3(3): 235-240. DOI:10.2514/3.22979 |
| [11] |
Kuhlmann T L, Peeters R L, Bills K W. Modified maximum principal stress failure criterion applied to propellant-liner bond failures[R]. AIAA-85-1439. 1985.
|
| [12] |
Mohr D, Oswald M. A new experimental technique for the multi-axial testing of advanced high strength steel sheets[J].
Experimental Mechanics, 2008, 48: 65-77. DOI:10.1007/s11340-007-9053-9 |
A multi-angle tensile clamp was designed for rectangular adhesive specimen according to QJ 2038.1A-2004. Pure tensile, pure shear and tensile-shear mixed stress conditions on the specimen interface were realized.