2. 南京理工大学理学院, 江苏 南京 210094
2. School of Science, NUST, Nanjing 210094, China
炮射智能弹药发展迅速, 已经成为现代战争不可或缺的弹药之一[1], 然而这类弹药抗过载能力有限。随行装药是与传统火炮发射技术相兼容, 又能显著提高火炮初速的有效装药技术[2-6]。国内外研究过的随行装药方案, 按其工作模式有捆绑式、弹底粘结式和包容式等[7-8]。但所有这些传统随行装药方案[3-8]在提高射弹初速的同时最终都将伴随射弹底部压力的明显增加, 也即伴随射弹过载的增加。对于智能弹药而言, 增加过载是不允许的。为了克服传统随行装药的固有缺陷, 本研究在汲取传统随行装药技术、脱壳弹设计技术和再生式液体发射药火炮(RLPG)技术[9]的优点基础上, 提出了一种基于差动原理的新型随行装药发射方案, 简称为差动随行装药方案。该装药方案不仅能在限定射弹过载条件下大幅度提高初速, 而且便于利用次口径脱壳弹技术减小飞行弹丸的飞行阻力, 从而有效增大射程。
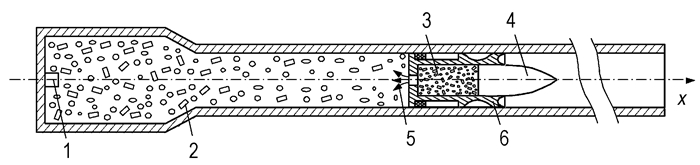
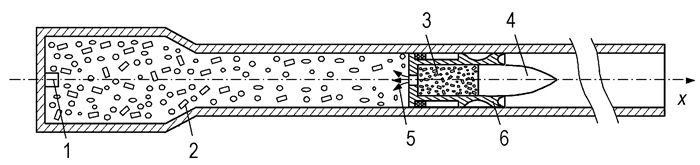
2 差动随行装药及发射过程理论模型 2.1 结构及原理图 1为研究提出的差动随行装药结构及其发射过程示意图。差动随行弹药由缸形底座、飞行弹丸(滑翔弹)和贮能室三部分组成, 贮能室内填充固体发射药。缸形底座在膛内工作期间相当于活塞缸, 出炮口后分离为卡瓣, 脱开飞行弹丸。它的底部开有喷射孔。差动随行弹药的设计应满足如下准则: ①缸形底座速度(或加速度)始终大于飞行弹芯的速度(或加速度); ②贮能室内随行装药及其燃气必须在指定位置(lk1≤0.75lg)喷射完毕; ③喷射进入弹后空间的随行药粒要求在指定位置(lk2≤0.85lg)燃烧完毕。满足该设计准则的相应数学表达式分别为:
|
图 1 差动随行装药结构及发射过程示意图 1—底火,2—药粒,3—贮能室,4—飞行弹丸(滑翔弹),5—射流,6—缸形底座 Fig.1 Schematic diagram of interior ballistic model of differential traveling charge firing concept 1—artillery primer, 2—powder grain, 3—energy storage chamber, 4—projectile(gliding projectile), 5—jet flow, 6—cylinder base |
| $ \frac{{{\rm{d}}{v_{{\rm{p2}}}}}}{{{\rm{d}}t}} > \frac{{{\rm{d}}{v_{{\rm{p1}}}}}}{{{\rm{d}}t}} $ | (1) |
| $ {l_{{\rm{k1}}}} \le 0.75{l_{\rm{g}}} $ | (2) |
| $ {l_{{\rm{k2}}}} \le 0.85{l_{\rm{g}}} $ | (3) |
其中
| $ {l_{{\rm{k1}}}} = \int_0^{{t_{{\rm{k1}}}}} {{v_{{\rm{p2}}}}{\rm{d}}t} $ | (4) |
| $ {l_{{\rm{k2}}}} = \int_0^{{t_{{\rm{k2}}}}} {{v_{{\rm{p2}}}}{\rm{d}}t} $ | (5) |
式中, vp1、vp2分别为缸形底座和飞行弹丸运动速度, m·s-1; tk1、tk2分别为随行药喷射结束时间和燃烧结束时间, s; lg为弹丸行程, m。运用差动原理, 即通过合理选择和匹配随行弹药各组合件结构、尺寸、质量(材料)、随行药品号、喷口打开时间与喷口尺寸大小, 使不同组合件所承受的推力和产生的加速度(速度)不同, 满足式(1)~(5)的要求, 迫使随行贮能室容积逐步压缩变小和自行喷射。同时通过控制随行药点火, 实现随行装药的点火延迟。当贮能室底部压强大于弹底压强时, 随行工质即可从喷射孔喷出实现向弹后空间加质加能。
这种情况下, 差动随行弹药的组合设计和内弹道优化设计依赖于全新的发射过程理论模型。本研究给出了差动随行弹药动力学模型。对于弹后空间即内弹道模型, 需要考虑随行后喷作用, 建立修正Lagrange假定条件下的内弹道方程组。限于篇幅, 仅扼要给出几个主要方程。
2.2 基本假定为建立差动随行装药发射过程理论模型, 提出如下假定:
(1) 忽略差动弹药沿身管运动过程中的章动影响, 忽略随行药及燃气的转动效应;
(2) 贮能室内工作介质沿轴向服从Lagrange分布;
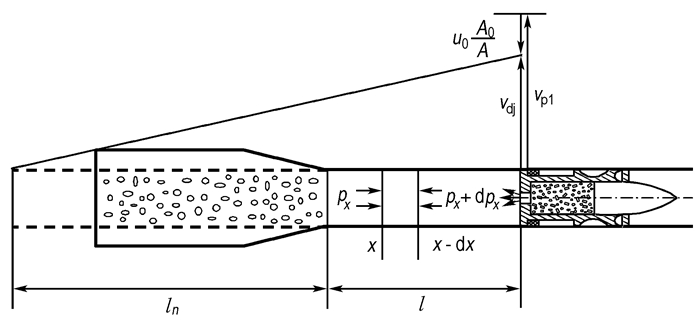
(3) 弹后空间采用修正的Lagrange假定, 工质密度呈均匀分布, 速度服从线性分布, 但应考虑随行工质后喷的影响(见图 2);
|
图 2 修正Lagrange假定条件下弹后空间介质速度沿轴向分布示意图 Fig.2 Schematic diagram of medium velocity distribution behind projectile based on modified Lagrange assumption |
(4) 不考虑贮能室变形及与边界的热交换;
(5) 其它假定与传统内弹道模型相同。
2.3 差动随行弹药动力学方程组(1) 缸形底座运动方程:
| $ \left( {A - {A_0}} \right){p_{\rm{d}}} - {A_2}{p_1} = {\varphi _1}{m_1}\frac{{{\rm{d}}{v_{{\rm{p1}}}}}}{{{\rm{d}}t}}\;\;\;\;\left( {{p_{\rm{d}}} > {p_0}} \right) $ | (6) |
式中, A、A0、A2分别为喷射孔面积、炮膛横截面积和贮能室内腔横截面积, m2; pd、p1分别为弹底压力和贮能室左端面压力, Pa; φ1为次要功系数, 无量纲; m1为缸形底座的质量, kg; p0为启动阻力, Pa。
(2) 飞行弹丸运动方程:
| $ {A_2}{p_2} = {m_2}\frac{{{\rm{d}}{v_{{\rm{p2}}}}}}{{{\rm{d}}t}} $ | (7) |
式中, p2为贮能室右端面压力, Pa; m2为飞行弹丸的质量, kg。
(3) 随行工质运动方程:
| $ {A_2}\left( {{p_1} - {p_2}} \right) + {{\dot m}_{\rm{t}}}{u_0} = {m_{\rm{t}}}\frac{{{\rm{d}}{v_{{\rm{tm}}}}}}{{{\rm{d}}t}} $ | (8) |
式中, vtm为随行工质平均速度, m·s-1; u0为喷孔燃气流出速度, m·s-1; mt为随行工质质量, kg; ṁt为喷孔流出的质量流量, kg·s-1。
(4) 随行工质质量mt:
| $ {m_{\rm{t}}} = {m_{{\rm{t0}}}} - \int_0^t {{{\dot m}_{\rm{t}}}{\rm{d}}t} $ | (9) |
式中, mt0为初始随行工质质量, kg。
(5) 喷孔流出的质量流量ṁt由气相质量流量和固相质量流量两部分组成, 因此有:
| $ {{\dot m}_{\rm{t}}} = {{\dot m}_{{\rm{tg}}}} + {{\dot m}_{{\rm{tp}}}} $ | (10) |
(6) 喷孔气相质量流量ṁtg:
| $ {{\dot m}_{{\rm{tg}}}} = {C_{{\rm{Dg}}}}{A_0}{\rho _{{\rm{gt}}}}\varepsilon {u_0} $ | (11) |
式中, CDg为气相流量系数, 无量纲; ρgt为喷孔流出的气相密度, kg·m-3; ε为空隙率, 无量纲。
(7) 喷孔颗粒相质量流量ṁtp:
| $ {{\dot m}_{{\rm{tp}}}} = {C_{{\rm{Dp}}}}{A_0}{\rho _{{\rm{pt}}}}\left( {1 - \varepsilon } \right){u_0} $ | (12) |
式中, CDp为固相流量系数, 无量纲; ρpt为随行工质密度, kg·m-3。
(8) 喷孔燃气流出速度u0:
| $ {u_0} = \left\{ \begin{array}{l} \sqrt {\frac{{2\gamma }}{{\gamma - 1}}{R_{\rm{t}}}{T_{\rm{g}}}\left[ {1 - {{\left( {\frac{{{p_{\rm{d}}}}}{{{p_{\rm{1}}}}}} \right)}^{\frac{{\gamma - 1}}{\gamma }}}} \right]} \;\;\;\;\;\;\left( {\frac{{{p_{\rm{d}}}}}{{{p_{\rm{1}}}}} > {{\left( {\frac{2}{{\gamma + 1}}} \right)}^{\frac{{\gamma - 1}}{\gamma }}}} \right)\\ {C_{\rm{a}}}\;\;\;\;\left( {\frac{{{p_{\rm{d}}}}}{{{p_{\rm{1}}}}} \le {{\left( {\frac{2}{{\gamma + 1}}} \right)}^{\frac{{\gamma - 1}}{\gamma }}}} \right) \end{array} \right. $ | (13) |
式中, γ为燃气比热比, 无量纲; Tg为贮能室内燃气温度, K; Ca为声速, m·s-1; Rt为燃气常数, J·(mol·K)-1。
(9) 贮能室气相密度ρgt:
| $ {\rho _{{\rm{gt}}}} = \frac{{{m_{{\rm{tg}}}}}}{{{A_2}{x_{\rm{t}}}\varepsilon }} $ | (14) |
式中, xt为贮能室空间长度, m。
(10)贮能室空隙率ε:
| $ \varepsilon = 1 - \frac{{{m_{{\rm{tp}}}}}}{{{\rho _{{\rm{pt}}}}{A_2}{x_{\rm{t}}}}} $ | (15) |
(11)贮能室空间长度xt:
| $ {x_{\rm{t}}} = {x_{{\rm{t0}}}} - \int_0^t {\left( {{v_{{\rm{p1}}}} - {v_{{\rm{p2}}}}} \right){\rm{d}}t} $ | (16) |
式中, xt0为贮能室长度初值, m。
(12)贮能室气相质量mtg:
| $ {m_{{\rm{tg}}}} = \int_0^t {\left( {{{\dot m}_{{\rm{tgc}}}} - {{\dot m}_{{\rm{tg}}}}} \right){\rm{d}}t} $ | (17) |
式中, ṁtgc为贮能室燃气生成速率, kg·s-1。
(13)贮能室固相质量mtp:
| $ {m_{{\rm{tp}}}} = {m_{{\rm{t0}}}} - \int_0^t {\left( {{{\dot m}_{{\rm{tg}}}} - {{\dot m}_{{\rm{tg}}}}} \right){\rm{d}}t} - {m_{{\rm{tg}}}} $ | (18) |
(14)贮能室燃气生成速率ṁtgc:
| $ {{\dot m}_{{\rm{tgc}}}} = \frac{{{m_{{\rm{tp}}}}}}{{1 - {\psi _{\rm{t}}}}}\frac{{{\rm{d}}{\psi _{\rm{t}}}}}{{{\rm{d}}t}} $ | (19) |
式中, ψt为随行药已燃体积比, 无量纲。
(15)贮能室留存随行药已燃体积比ψt[10]:
| $ {\psi _{\rm{t}}} = \left\{ \begin{array}{l} \chi {z_{\rm{t}}}\left( {1 + \lambda {z_{\rm{t}}} + \mu z_{\rm{t}}^2} \right)\;\;\;\;\;\left( {0 \le {z_{\rm{t}}} \le 1} \right)\\ {\chi _{\rm{s}}}{z_{\rm{t}}}\left( {1 + {\lambda _{\rm{s}}}{z_{\rm{t}}}} \right)\;\;\;\;\;\;\;\left( {1 < {z_{\rm{t}}} \le {z_{\rm{k}}}} \right) \end{array} \right. $ | (20) |
式中, χ、λ、μ为随行药药形系数, 无量纲; χs、λs为随行药分裂碎块药形系数, 无量纲; Zt为相对已燃弧厚, 无量纲。
(16)随行药相对已燃弧厚zt[10]:
| $ \frac{{{\rm{d}}{z_{\rm{t}}}}}{{{\rm{d}}t}} = \frac{{{u_1}}}{{{e_1}}}p_{{\rm{tm}}}^{\rm{n}} $ | (21) |
式中, e1为随行药初始弧厚的一半, m; u1为燃速系数, m·s-1; n为燃速指数, 无量纲; ptm为贮能室平均压力, Pa。
(17)贮能室平均压强ptm:
| $ {p_{{\rm{tm}}}} = {p_1} - \frac{1}{2}{\rho _{\rm{t}}}\bar M{x_{\rm{t}}} - \frac{1}{6}{\rho _{\rm{t}}}\bar Nx_{\rm{t}}^2 $ | (22) |
式中,M、N为组合量, 分别为:
| $ \bar M = \frac{{\left( {A - {A_0}} \right){p_{\rm{d}}} - {A_2}{p_1}}}{{{\varphi _1}{m_1}}} + \frac{{{v_{{\rm{p1}}}}\left( {{v_{{\rm{p2}}}} - {v_{{\rm{p1}}}}} \right)}}{{{x_{\rm{t}}}}} $ | (23) |
| $ \bar N = \frac{1}{{{x_{\rm{t}}}}}\left[ {\frac{{{A_2}{\rho _2}}}{{{m_2}}} - \frac{{\left( {A - {A_0}} \right){p_{\rm{d}}}}}{{{\varphi _1}{m_1}}} + \frac{{{A_2}{p_1}}}{{{\varphi _1}{m_1}}}} \right] $ | (24) |
(18)贮能室混合密度ρt:
| $ {\rho _{\rm{t}}} = \frac{{{m_{{\rm{tg}}}} + {m_{{\rm{tp}}}}}}{{{A_2}{x_{\rm{t}}}}} $ | (25) |
(19)弹芯底部压强p2:
| $ {p_2} = {p_1} - {\rho _{\rm{t}}}\bar M{x_{\rm{t}}} - \frac{1}{2}{\rho _{\rm{t}}}\bar Nx_{\rm{t}}^2 $ | (26) |
(20)贮能室气体状态方程:
| $ {p_{{\rm{tm}}}}\left( {{A_2}{x_{\rm{t}}} - \frac{{{m_{{\rm{tp}}}}}}{{{\rho _{{\rm{pt}}}}}} - {m_{{\rm{tg}}}}{\alpha _{\rm{t}}}} \right) = {m_{{\rm{tg}}}}{R_{\rm{t}}}{T_{\rm{g}}} $ | (27) |
式中, αt为随行药气体余容, m3/kg。
(21)贮能室能量守恒方程:
| $ \begin{array}{l} {A_2}{x_{\rm{t}}}\left[ {{\rho _{{\rm{gt}}}}\varepsilon {h_{\rm{g}}} + {\rho _{{\rm{pt}}}}\left( {1 - \varepsilon } \right){h_{\rm{p}}}} \right] = \frac{1}{\theta }\int_0^1 {f{{\dot m}_{{\rm{tgc}}}}{\rm{d}}t} - \\ \int_0^1 {{{\dot m}_{{\rm{tg}}}}{h_{\rm{g}}}{\rm{d}}t} - \int_0^1 {{{\dot m}_{{\rm{tp}}}}{h_{\rm{p}}}{\rm{d}}t} + {A_2}\int_0^t {{p_1}{v_{{\rm{p1}}}}{\rm{d}}t} - {A_2}\int_0^t {{p_2}{v_{{\rm{p2}}}}{\rm{d}}t} \end{array} $ | (28) |
式中,hp、hg分别为随行药及其燃气比焓, Pa·m3; f为随行药火药力, J·kg-1; θ=γ-1, γ为比热比, 无量纲。
2.4 弹后空间主要内弹道方程(22)流入弹后的随行药生成燃气质量mtgo:
| $ {m_{{\rm{tgo}}}} = \int_0^t {\left( {{{\dot m}_{{\rm{tg}}}} + {{\dot m}_{{\rm{tgi}}}}} \right){\rm{d}}t} $ | (29) |
(23)流入弹后的随行固相质量mtpo:
| $ {m_{{\rm{tpo}}}} = \int_0^t {\left( {{{\dot m}_{{\rm{tp}}}} + {{\dot m}_{{\rm{tgi}}}}} \right){\rm{d}}t} $ | (30) |
(24)流入弹后的随行药气体生成速率ṁtgi:
| $ {{\dot m}_{{\rm{tgi}}}} = \frac{{\int_0^t {{{\dot m}_{{\rm{tp}}}}} {\rm{d}}t}}{{1 - {\psi _{\rm{t}}}}}\frac{{{\rm{d}}{\psi _{\rm{t}}}}}{{{\rm{d}}t}} $ | (31) |
(25)弹底工质速度修正值vdj:
| $ {v_{{\rm{dj}}}} = \frac{{\left( {\sum\limits_{i = 1}^N {{\omega _{\rm{i}}}} } \right){v_{{\rm{p1}}}} - 2\int_0^t {{{\dot m}_{\rm{t}}}{v_0}} {\rm{d}}t}}{{\sum\limits_{i = 1}^N {{\omega _{\rm{i}}}} + \int_0^t {{{\dot m}_{\rm{t}}}} {\rm{d}}t}}\left( {i = 1,2, \cdots {\rm{N}}} \right) $ | (32) |
式中,ωi为第i种主装药量, kg。
(26)喷孔后喷流体相对身管的速度v0:
| $ {v_0} = {v_{{\rm{p1}}}} - {u_0} $ | (33) |
(27)内弹道基本方程
| $ \begin{array}{l} \sum\limits_{i = 1}^N {{f_{\rm{i}}}{\omega _{\rm{i}}}{\psi _{\rm{i}}} + {f_{\rm{t}}}{m_{{\rm{tgo}}}}} - Ap\left( {l + {l_\psi }} \right) = \frac{\theta }{2}\left( {{\varphi _1}{m_1}v_{{\rm{p1}}}^2 + {m_2}v_{{\rm{p2}}}^2 + } \right.\\ \left. {{m_{\rm{t}}}v_{{\rm{tm}}}^2} \right) + \frac{\theta }{6}\left( {\sum\limits_{i = 1}^N {{\omega _{\rm{i}}}} + \int_0^t {{{\dot m}_{\rm{t}}}} {\rm{d}}t} \right)v_{{\rm{dj}}}^2 \end{array} $ | (34) |
式中, fi为第i种主装药火药力, J·kg-1; l为弹丸行程, m; lψ为药室有效自由空间缩颈长, m。
(28)弹后空间压力分布px:
| $ {p_{\rm{x}}} = {p_{\rm{d}}} + \frac{{\sum\limits_{i = 1}^N {{\omega _{\rm{i}}}\frac{{{\rm{d}}{v_{{\rm{p1}}}}}}{{{\rm{d}}t}} - {{\dot m}_{\rm{t}}}\left( {2{v_0} + {v_{{\rm{dj}}}}} \right)} }}{{2A{{\left( {l + {l_0}} \right)}^2}}}\left[ {{{\left( {l + {l_0}} \right)}^2} - {x^2}} \right] $ | (35) |
式中,l0为药室缩颈长, m。
3 差动随行装药发射过程计算分析基于上述理论模型, 采用龙格-库塔法[11]编程进行数值求解。对160 mm口径火炮采用表 1基本参量, 其中主要约束条件为最大膛压pm、飞行弹丸底部最大压力p2m和弹丸行程长lg, 通过调节主装药量ωi、随行药量mt0及其药形与弧厚2e1i等, 得到的结果如表 2。计算中, 选择的优化参量为弹丸初速v0和身管工作容积利用率ηg。有必要说明, 表中缸形底座质量m1是影响计算结果的一个重要参量, 在本研究条件下, 经简单估算, 取m1=2.0+0.5mt0, 单位为kg, 其右端第一项考虑了它应具有的基本质量, 第二项考虑了所携带的随行药量对它的影响。表 2中pg为炮口处压力。
| 表 1 计算用基本参量一览表 Tab.1 Primary parameters of 160 mm gun for calculation |
| 表 2 内弹道计算结果 Tab.2 Calculated results of interior ballistic |
表 2中的方案1~3, 以保持飞行弹丸底部最大压力p2m和总弹重mq=m1+m2=50kg不变为前提, 调整缸形底座质量m1、飞行弹丸质量m2和随行药量mt0。计算结果表明, 随着mt0的增大, 弹丸初速v0和身管工作容积利用率ηg都明显增大。如方案3, mt0=9.2 kg, 主装药量ωi=13.41 kg, 当总装药量(Σωi+mt0)相对常规装药(Σωi)增加约7.1 kg时, 初速提高了247 m·s-1, 其增幅约为26%, 身管工作容积利用率ηg增大约28%。
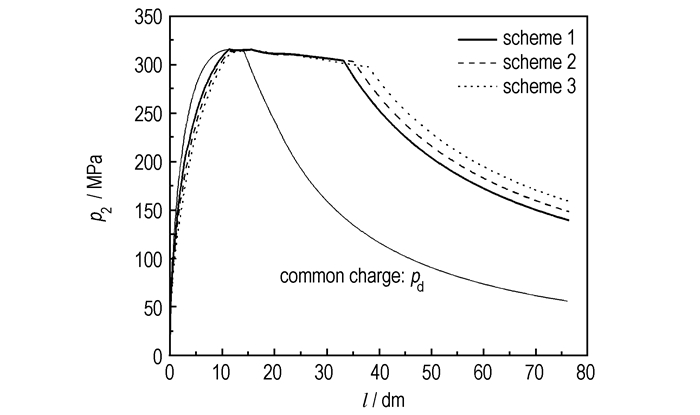
身管工作容积利用率ηg及初速v0的增加, 归功于压力分布的改善。从图 3和图 4所示弹底压力-弹丸行程曲线(p2-l曲线)上可以看到这一点。对于常规装药, 当弹底压力上升至最大点之后, 压力呈快速下降趋势。而差动随行装药通过适当调整主装药和随行药药量的比例, 特别通过随行装药自行向弹后持续加质加能, 弹底压力即使过了最大点, 其下降趋势也比较缓慢, 即形成平台效应。由图 3和图 4可见, 随着随行药量mt0增大, 压力曲线下面积不断增大, 即身管工作容积利用率不断提高, 因此弹丸初速必然随之上升。
|
图 3 方案1~3的p2-l曲线 Fig.3 p2-l curves of scheme 1 to 3 |
|
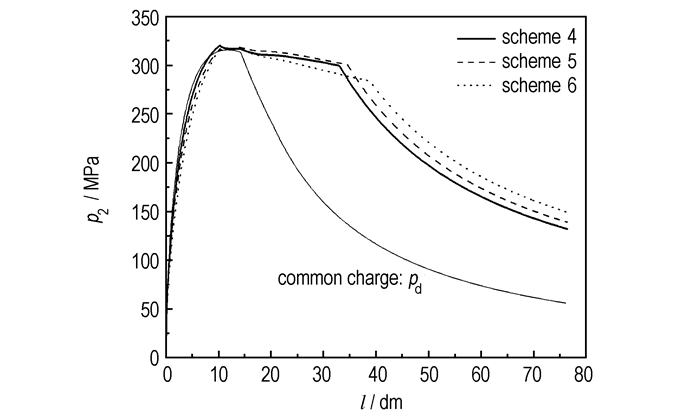
图 4 方案4~6的p2-l曲线 Fig.4 p2-l curves of scheme 4 to 6 |
表 2中的方案4~6, 取飞行弹丸质量m2=50 kg不变, 发射总弹重随着随行药量的增加而增加。计算结果表明, 尽管缸形底座质量的存在明显增大了发射的组合弹丸总重量, 但差动随行发射方案仍然取得了约16%左右的增速效果。在这里特别指出, 所有这些计算都是以不增加飞行弹丸底部最大压力p2m为前提的, 因为对炮射智能弹药而言, 射弹承受的最大过载或承受的最大压力是限定的, 只有在这种前提下讨论提高初速和射程才是有意义的。
4 射程估算由上述可知, 差动随行装药可以在不增加射弹过载的前提下大幅度地提高射弹初速。在此基础上, 如果再采用次口径脱壳弹设计技术, 即取飞行弹丸直径小于炮膛内径, 优化弹形设计, 提高射弹升阻比, 则可使射弹射程大幅增加。即在内弹道阶段, 利用差动随行发射原理, 使飞行弹丸获得较大的炮口速度; 射弹出炮口后, 缸形底座与飞行弹丸自动分离; 在外弹道阶段, 由于飞行弹丸直径小于火炮身管直径, 具有优化的气动特性, 不仅飞行阻力较小, 而且具有较好的滑翔功能, 最终能使火炮射程显著地提高。
取发射的飞行弹丸直径d2=130 mm, 按低旋尾翼稳定滑翔弹设计。在此基础上, 采用修正质点外弹道模型[12]计算射程, 计算中不同高程区间取不同标准气象条件。计算结果表明, 对应于表 2中方案3, 射弹质量m2=43.4 kg, 初速v0=1204.6 m·s-1, 射程可达99 km; 而常规装药发射50 kg弹重、957.5 m·s-1初速的射程约为64 km, 因此, 表 2中方案3比常规装药的射程增加了35 km。对应于表 2中的方案6, 射弹质量m2=50 kg时, 初速v0=1117.0 m·s-1, 其射程可达89 km, 相对常规装药增加约25 km。
5 结论提出了一种以火炮为平台发射智能弹药提高初速的新型随行装药方案。这方案基于再生式液体炮(RLPG)及差动原理提出的发射技术, 其主要优点和功能在于:在限定的射弹过载条件下, 能大幅度提高火炮工作容积利用率和初速, 并且便于与次口径脱壳弹设计技术相匹配, 飞行弹丸可采用高升阻比滑翔弹弹形, 为进一步增大火炮射程提供了有利条件。建立了差动随行装药火炮内弹道理论模型。计算表明, 对口径d=160 mm火炮, 身管长lg=7.64 m, 总弹重mq=50 kg, 飞行弹丸质量m2=43.4 kg, 随行药量mt0=9.2 kg, 身管工作容积利用率可提高28%;初速可提高26%。相应射程可增大到99 km, 比常规装药增大了约35 km。本文研究为提高炮射智能弹初速和射程提供了理论支持。
| [1] |
杨绍卿.
灵巧弹药工程[M]. 北京: 国防工业出版社, 2010.
YANG Shao-qing. Smart muntion engineering[M]. Beijing: National Defense Industry Press, 2010 |
| [2] |
邹华, 张领科, 周彦煌. 采用组合发射提高某型火炮初速的理论研究[J].
火炸药学报, 2013, 36(2): 69-75. ZOU Hua, ZHANG Ling-ke, ZHOU Yan-huang. Theoretical study of increasing projectile initial velocity by using combined firing[J]. Chinese Journal of Explosives & Propellants, 2013, 36(2): 69-75. |
| [3] |
赵博文, 余永刚, 潘玉竹. 随行装药退火算法的优化设计及数值模拟[J].
火炸药学报, 2010, 33(5): 75-78. ZHAO Bo-wen, YU Yong-gang, PAN Yu-zhu. Numerical simulation and optimization design on annealing algorithm of traveling charge[J]. Chinese Journal of Explosives & Propellants, 2010, 33(5): 75-78. |
| [4] |
杨京广, 余永刚. 随行装药内弹道一维气动力模型及数值模拟[J].
火炸药学报, 2009, 32(1): 13-16. YANG Jing-guang, YU Yong-gang. The one-dimensional interior ballistic aerodynamic model and numerical simulation of traveling charge[J]. Journal of Explosives & Propellants, 2009, 32(1): 13-16. |
| [5] |
杨京广, 余永刚. 随行装药方案提高大口径火炮初速的数值预测[J].
爆炸与冲击, 2008, 28(2): 161-165. YANG Jing-guang, YU Yong-gang. Velocity prediction of big caliber gun based on traveling charge scheme[J]. Explosion and Shock Waves, 2008, 28(2): 161-165. DOI:10.11883/1001-1455(2008)02-0161-05 |
| [6] |
周彦煌, 王升晨. 120mm反坦克炮采用随行装药提高初速的理论研究[J].
兵工学报, 1995(3): 5-10. ZHOU Yan-huang, WANG Sheng-chen. A theoretical study of muzzle velocity augmentation with traveling charges in the 120 mm anti-tank Gun[J]. Acta Armamentarii, 1995(3): 5-10. |
| [7] |
周彦煌. 固体随行装药内弹道理论模型. 弹道学术会议论文集[C]//厦门: 中国兵工学会-弹道学会, 1992: 23-33.
ZHOU Yan-huang. Interior ballistic model of solid traveling charge. Ballistic Academic Conference Papers[C]//Xiamen: China Ordnance Society-Ballistic Society, 1992: 23-33. |
| [8] |
王浩. 随行装药理论研究与实验技术方案[D]. 南京: 南京理工大学博士论文, 1992.
WANG Hao. Theory study and experiment technique scheme of traveling charge[D]. Nanjing: Nanjing University of Science and Technology, 1992. |
| [9] |
Coffee T P. A combined lumped parameter/one-dimensional blowdown model for the regenerative liquid propellant gun. Technical Report AD-A251779[R], BRL-TR-3364, U S Army Ballistic Research Laboratory, 1992.
|
| [10] |
金志明.
高速推进内弹道学[M]. 北京: 国防工业出版社, 2001.
JIN Zhi-ming. Interior ballistics of hypervelocity propulsion[M]. Beijing: National Defense Industry Press, 2001 |
| [11] |
黄明游, 刘播, 徐涛.
数值计算方法[M]. 北京: 科学出版社, 2009.
HUANG Ming-you, LIU Bo, XU Tao. Numerical computation method[M]. Beijing: Science Press, 2009 |
| [12] |
宋丕极.
枪炮与火箭外弹道学[M]. 北京: 兵器工业出版社, 1993.
SONG Pi-ji. Exterior ballistics of guns and rockets[M]. Beijing: Weapon Industry Press, 1993 |
A new firing concept based on differential traveling charge technology can largely increase gun launched intelligent ammunition muzzle velocity, and improve gun working volume utilization rate.



