燃料空气炸药(Fuel-Air-Explosive, FAE)是近几十年来发展起来的新型炸药, 具有超压衰减缓慢、作用面积大等优点, 同时能够产生热辐射、缺氧、地震波等多种毁伤因素, 因而成为国内外研究的热点。FAE装置先由中心管内的高能炸药起爆, 驱动燃料分散形成云雾, 然后二次起爆实现爆轰。因此, 燃料分散的效果对FAE爆炸威力具有重要影响。张奇等就FAE装置中心装药量对燃料成雾特性进行了实验研究[1], 发现中心装药对燃料的抛散半径具有临界值; 同时对FAE装置在近场的抛撒速度进行了理论推导[2]; 罗艾民等[3]对爆炸驱动固体颗粒的分散作用进行了理论分析, 惠君明等[4]对FAE装置的云雾控制进行了研究。然而, 在相同的FAE装置条件下, 耦合装药与不耦合装药孰优孰劣, 却没有相关报道。同时, FAE在爆炸初期, 二次起爆之前, FAE装置内部的动力学演化过程究竟处于怎样的状态, 也没有学者进行深入研究。
基于此, 本研究利用LS-DYNA对中心装药采用耦合装药方式的FAE装置的燃料抛散速度的最大值进行了计算, 并利用高速相机对其进行了测定。进而采用相同的计算方法对中心装药采用不耦合装药方式的FAE装置的抛散速度、爆炸空腔、空腔温度进行了研究和分析。
2 试验测定试验利用高速相机观测燃料的分散特性。试验装置布置如图 1所示。在试验中, 将高速摄像机正对FAE装置中轴, 两侧标杆对称放置。试验时, 高速相机记录到每一时刻燃料云雾分散的云团, 如图 2所示。将每一时刻燃料云团的最大宽度作为这一时刻的云雾分散直径。利用标杆间距作为参考, 就可得到不同时刻燃料云雾分散的半径, 结合高速相机的拍摄时间, 即可得到不同时刻燃料的抛散速度。经试验测定, 当采用耦合装药时, 燃料抛散速度的最大值为408.5 m·s-1。

|
图 1 试验装置布置示意图 1—高速相机, 2, 3—测量标杆, 4—FAE装置 Fig.1 Sketch of experimental instrument arrangement 1—high speed photography, 2, 3—symbol pole, 4—FAE device |

|
图 2 燃料抛散云图 Fig.2 Picture of fuel dispersal |
由于模型本身是具有对称性的圆柱体, 计算模型采取1/4模型进行计算, 壳体外径108 mm, 壳体内径105 mm, 中心管外径18 mm, 中心管内径16 mm, 壳体净高290 mm, 上下端板厚10 mm, 中心管壳体厚度为2 mm, 外部壳体厚度为3 mm。
计算模型共有四个, 对其进行编号, 分别为1#、2#、3#、3(T)#。四种中心装药的装药量如表 1所示。四种中心装药尺寸及结构如图 3所示。其中1#模型采用耦合装药, 2#、3#、3(T)#号模型采用不耦合装药, 2#模型的不耦合系数De=2, 3#模型的不耦合系数De=3, 3(T)#模型采用“T”形装药, “T”形装药的药量与不耦合系数为3时相等, 中间装药部分直径Φ=10 mm, 两端对称部分直径Φ=16 mm。采用“T”形装药的目的是为了比较柱形不耦合装药与“T”形不耦合装药在燃料抛散方面的优劣。
| 表 1 四种装药结构的装药量 Tab.1 Charge mass of four kinds of explosive |

|
图 3 四种中心装药尺寸及结构(单位: mm) 1—壳体, 2—燃料, 3—空气, 4—中心装药 Fig.3 Size and structure of four kinds of center explosive charges(unit: mm) 1—shell, 2—fuel, 3—air, 4—center explosive charge |
计算采用LG-DYNA软件中的流固耦合算法[5], 网格边长控制在1 mm左右, 最小网格尺寸为1 mm×1 mm×1 mm, 单元总数为1210000。计算时间为1500 μs, 步长为0.6 μs。单元采用单点积分的ALE多物质单元, 即一个单元内可以包含多种物质。炸药、燃料和空气区采用Euler网格, 中心管及壳体采用Lagrange网格[5], 划分的网格如图 4所示。网格的大小和质量会影响计算的结果, 当划分的网格增大一倍时, 即1 mm×1 mm×2 mm时, 以1#模型(De=1)为例, 计算得到的最外层燃料抛散速度为277 m·s-1, 与实验测定值相差很大, 而当采用1 mm×1 mm×1 mm网格时, 计算所得到的燃料抛散速度的最大值为412.5 m·s-1, 和实验测定的速度相当吻合。图 5是以FAE装置的中心为基点, 沿轴向(Z方向)每间隔5 cm选取的观测点, 便于提取不同位置处燃料抛散的数据。

|
图 4 模型整体网格图 Fig.4 Grid of the model |

|
图 5 燃料观测点选取示意图 Fig.5 Observation points of the fuel |
计算中TNT炸药采用HIGH_EXPLOSIVE_BURN模型[6], 用EOS_JWL状态方程进行描述, 其具体形式为:
| $ p = {A_1}\left[{1-\frac{\omega }{{{R_1}V}}} \right]{{\rm{e}}^{ - {R_1}V}} + {B_1}\left[{1-\frac{\omega }{{{R_2}V}}} \right]{{\rm{e}}^{ -{R_2}V}} + \frac{E}{V} $ | (1) |
式中, A1、B1、R1、R2为与炸药性质有关的常数; p为压力, Pa; E为单位体积炸药的内能,J·m-3; V为相对比体积,初始值为1。对于TNT炸药取A1=374 GPa; B1=7.33 GPa; R1=4.15; R2=0.90; ω=0.3; E=7.0×109 J·m-3。TNT的密度为1630 kg·m-3; 爆速为6930 m·s-1[6]。
空气采用NULL材料模型以及用LINEAR_POLYNOMIAL状态方程描述[7]。线性状态方程为:
| $ p = {c_0} + {c_1}\mu + {c_2}{\mu ^2} + {c_3}{\mu ^3} + \left( {{c_4} + {c_5}\mu + {c_6}{\mu ^2}} \right)E $ | (2) |
式中, p为爆轰压力, Pa; E为空气的单位体积内能, 初始值为2.5×10-6 J·m-3; μ=1/V-1, V为相对比体积, 初始值为1。当线性多项式状态方程用于空气模型时, c0=-0.1 MPa; c1=c2=c3=c6=0; c4=c5=0.4;空气的密度取1.29 kg·m-3[8]。
燃料采用MAT_NULL材料模型和Gruneisen状态方程描述[9], Grunesien方程的具体形式如下:
| $ p = \frac{{{\rho _0}{C^2}\mu \left[{1 + \left( {1-\frac{{{\gamma _0}}}{2}} \right)\mu-\frac{\alpha }{2}{\mu ^2}} \right]}}{{\left[{1-\left( {{S_1}-1} \right)\mu-{S_2}\frac{{{\mu ^2}}}{{\mu + 1}} - {S_3}\frac{{{\mu ^3}}}{{{{\left( {\mu + 1} \right)}^2}}}} \right]}} + \left( {{\gamma _0} + \alpha \mu } \right)E $ | (3) |
式中, p为压力, Pa; E为单位体积内能, J·m-3; μ=ρ/ρ0-1, ρ0为燃料初始密度, ρ为扰动后的密度; C为燃料中声速; γ0为Gruneisen系数; S1, S2, S3为Vs-Vp斜率系数; α为体积修正系数。各个参数的具体值为: E=265 J·kg-1; ρ0=1130 kg·m-3; C =1650 m·s-1; S1=1.92; S2=-0.96; S3=0.2268; γ0=0.35; α=1.3937 [8]。
壳体材料为硬质PVC, 采用MAT_PLASTIC_KINEMATIC材料模型[7], 具体材料参数为:密度ρ0=1300 kg·m-3; 抗拉强度σ=32MPa[9]; 泊松比γ=0.38[9]。
4 结果与讨论 4.1 燃料抛散速度计算结果及分析选取1号模型(耦合装药, De=1)轴向距离Z=15.5 cm处的燃料进行观测, 其径向抛散速度-时间曲线如图 6所示。试验所测得的抛散速度最大值为408.5 m·s-1, 计算值为412.5 m·s-1, 误差不足1%, 试验测定值与计算值吻合度高, 验证了数值模拟方法和参数设置的正确性和可靠性。因此在FAE装置整体几何尺寸不变, 采用相同的计算方法和材料参数计算得到的其他不耦合装药的结果也是可靠的。

|
图 6 1#模型(De=1)轴向距离15.5 cm处燃料径向抛撒速度-时间曲线 Fig.6 Velocity curve of the fuel at axial distance of 15.5 cm for sample 1#(De=1) |
取不同轴向距离处燃料抛散速度的最大值进行绘图, 如图 7。由图 7发现, 当采用耦合装药时(De=1), 最外层燃料抛散速度的最大值出现在FAE装置端部, 而当采用不耦合装药时(De=2, 3, 3(T)), 最外层燃料抛散速度的最大值出现在FAE装置的中部。显然, 从燃料分散的角度考虑, 在满足设计要求的前提下, 应尽量采用不耦合装药, 以便于燃料抛散速度的最大值出现在FAE装置的中部, 形成半径尽可能大的扁平状云雾, 减少燃料在竖直方向上的分布, 提高燃料利用率。

|
图 7 不同中心装药在不同轴向距离处燃料抛散速度的最大值 Fig.7 Maximum velocity of the fuel for 4 center explosive charges at different axial distance |
比较图 7中耦合装药和不耦合装药FAE装置燃料抛散速度沿轴向的分布情况, 还可以发现, 当采用耦合装药时, FAE装置两端燃料的最大抛散速度要远远小于靠近中部位置燃料的最大抛散速度, 二者的差值接近200 m·s-1; 而当采用不耦合装药时, FAE装置两端燃料的最大抛散速度与靠近中部位置燃料的最大抛散速度相差较小, 约100 m·s-1, 可见燃料整体的速度比较均匀, 燃料的利用率有所提高。比较不耦合装药De=3时的柱形装药和“T”形装药的燃料抛散速度沿轴向的分布可以发现, 采用“T”形中心装药的FAE装置端部燃料的抛散速度与中部燃料的抛散速度差值大于同等情况下采用柱形装药的FAE装置, 从燃料抛散的角度分析, “T”形装药相对于柱形装药并不具备明显的优势。
取径向处不同径向距离处燃料抛散速度的最大值进行绘图, 如图 8。对比不同装药在不同径向距离处, 装置中部燃料抛散速度的最大值变化曲线可以发现, 当采用耦合装药时, 随着距离中心管距离的不断增加, 燃料的径向抛散速度呈下降趋势; 而采用不耦合装药时, 燃料的径向抛散速度呈现先减小后增大的趋势。这说明采用耦合装药时燃料在加速的初期并没有发生破碎, 而采用不耦合装药时, 燃料在加速阶段已经发生破碎。

|
图 8 不同中心装药在不同径向距离处FAE装置中部燃料抛散速度 Fig.8 Velocity of the fuel in the middle of the FAE with different center explosive charges at different radial distance |
为了研究爆炸空腔的扩张情况, 为FAE装置的设计提供理论支撑, 在计算结果中又提取了不同装药情况下爆炸空腔的图像进行分析。图 9是1#模型(De=1, 耦合装药)在不同时刻爆炸空腔的扩张形状, 为便于比较, 选取不耦合装药的3#模型(De=3)爆炸空腔的扩张图像, 如图 10所示。比较图 9和图 10不难发现, 两者在爆炸初期的扩张区域基本一致, 但不耦合装药(图 10)的空腔在后期逐渐的开始呈现中间大两端小的情况。

|
图 9 1#模型(De=1)不同时刻爆炸空腔的扩张图 Fig.9 Explosion cavity of sample 1#(De=1)at different time |

|
图 10 3#模型(De=3)不同时刻爆炸空腔的扩张图 Fig.10 Explosion cavity of sample 3#(De=3)at different time |
为便于定量分析, 沿轴向依次取5.5, 10.5, 15.5, 20.5, 25.5 cm五个观测点, 以燃料抛散速度在加速震荡过程中, 速度达到最小时为判据, 最大空腔半径分布情况如图 11。由图 11可发现, 采用耦合装药(De=1)的FAE装置的爆炸空腔半径在装置下部和中部大小基本一致, 均为0.5 m左右, 只是在接近装置顶端时空腔半径才略微变小; 采用不耦合装药的2#模型(De=2)最大空腔半径为0.27 m, 端部空腔半径为0.18 m, 半径缩小1/3, 3#模型(De=3)的最大空腔半径约为0.18 m, 端部空腔半径约为0.125 m, 也缩小了1/3左右。可见, 采用不耦合装药的FAE装置的爆炸空腔呈现出中间大, 两端小的分布, 且空腔半径较小。由于空腔内的高温高压很容易对二次起爆的药包造成影响, 因此, 在设计二次起爆药包的安装位置时, 要尽量避免其和爆炸空腔的接触, 显然采用不耦合装药的FAE装置在这方面具有极大的优势, 不但可以在装置的上端, 还可以在装置的下端设计二次起爆药包。

|
图 11 不同中心装药情况下轴向不同距离处爆炸空腔半径 Fig.11 Explosion cavity of different center explosive charges in different axial distance |
为分析一次起爆之后二次起爆之前, 爆炸空腔内的温度变化, 又进行了温度效应分析。
由于中心药采用的是TNT, 其爆轰产物的HOM的状态方程为[10]:
| $ \begin{array}{l} \ln (p) =-3.65769-2.475871(\ln V) + 0.2187351{(\ln V)^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;0.06225968{(\ln V)^3} + 0.01829405{(\ln V)^4} \end{array} $ | (4) |
| $ \begin{array}{l} \ln (T) = 7.5722-0.4432783(\ln V) + 0.09328338{(\ln V)^2} + \\ \;\;\;\;\;\;\;\;\;\;\;0.002578583{(\ln V)^3}-0.003187935{(\ln V)^4} \end{array} $ | (5) |
| $ \begin{array}{l} \ln (E) =-1.515413 + 0.5362583(\ln p) + 0.09738766{(\ln p)^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;0.009284769{(\ln p)^3} + 0.0003495791{(\ln p)^4} \end{array} $ | (6) |
式中, p为压力, Pa; V为比体积, V=1/ρ; E为比内能, J·m-3; T为温度, K。
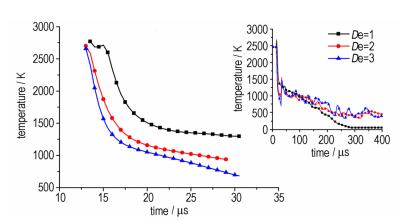
根据状态方程(4)(5)(6), 只需求出爆轰产物密度即可求出空腔内部的温度变化, 取装药中心处为观测点, 不同中心装药情况下观测点处爆轰产物密度变化如图 12。前期密度没有发生变化的原因是爆炸还没有传播到观测点处, 从图形结果分析, 炸药经历了冲击绝热压缩到爆轰作用阶段(CJ态爆轰产物密度大于炸药本身密度)、爆轰产物等熵膨胀密度迅速降低阶段, 这一点与经典爆轰理论[11]的描述是相吻合的; 不同装药情况下, 爆轰产物区内同一位置处爆轰产物变化趋势具有一致性, 但密度分布和密度变化率不完全相同, 根据式(5)可以计算出不同中心装药情况下爆轰产物内部的温度变化, 如图 13。

|
图 12 不同中心装药情况下爆轰产物的密度时间历程 Fig.12 Detonation products density of different center explosive charges at different time |

|
图 13 不同中心装药情况下爆轰产物的温度时间历程 Fig.13 Temperature of different center explosive charges at different time |
分析图 13可知, 无论采用哪种装药方式, 爆炸所产生的温度峰值基本相同; 但在13~28 μs这15 μs时间内, 采用耦合装药的1#模型(De=1)空腔内部的温度下降了1400K, 而采用不耦合装药的2#模型(De=2)和3#模型(De=3)空腔内的温度在相同的时间内则分别下降了1750 K和1900 K, 显然, 采用不耦合装药的FAE装置爆炸空腔内的温度下降得更快; 同时采用耦合装药时, 爆炸空腔内部的温度下降到1000 K左右时, 会出现一个“平台期”, 即空腔内部的温度会在空腔破裂之前在较高温度停留较长的时间, 这样就会对燃料进行长时间的加热; 而且随着时间的增加, 耦合装药爆炸空腔内的温度快速降低, 如图 13中小图部分所示, 说明耦合装药爆炸所形成的空腔发生破裂, 这样就造成空气的进入, 就有可能在二次起爆之前引燃燃料, 造成FAE装置能量的不正确释放, 降低FAE装置的威力。因而, 采用不耦合装药的FAE装置具有较高的安全性。
5 结论建立了数值计算模型, 得到FAE装置燃料的抛散速度、中心装药的爆炸空腔及腔内温度的变化规律, 得出如下结论:
(1) 在满足抛散需要的前提下, 中心装药应尽量采用不耦合装药, 这样既有利于燃料的抛散, 又有利于提高燃料的利用率, 从而在有限的装药情况下, 获得尽可能大的杀伤效果。
(2) 计算条件下, 采用耦合装药的FAE装置的爆炸空腔半径在装置下部和中部基本一致, 均为0.5 m左右, 只是在接近装置顶端时空腔半径才逐渐变小; 采用不耦合装药的FAE装置的爆炸空腔呈现出中间大, 两端小的分布, 且空腔半径较小。因而, 采用不耦合装药的FAE装置在二次起爆药包安装位置的选择上有更大的灵活性。
(3) 采用不耦合装药的FAE装置中心装药爆炸所形成的空腔内部温度下降的较快, 持续时间更短, 有较高的安全性。
| [1] |
张奇, 覃彬, 白春华, 等. 中心装药对FAE燃料成雾特性影响的实验分析[J].
含能材料, 2007, 15(5): 447-450. ZHANG Qi, QIN Bin, BAI Chun-hua, et al. Effect of total energy of center explosive charge on fuel dispersal characteristic feature[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2007, 15(5): 447-450. |
| [2] |
ZhANG Qi, BAI Chun-hua, LIU Qing-ming, et al. Study on near field dispersal of fuel air explosive[J].
Journal of Beijing Institute of Technology, 1999, 8(2): 113-118. |
| [3] |
罗艾民, 张奇, 李建平, 等. 爆炸驱动作用下固体燃料分散过程的计算分析[J].
北京理工大学学报, 2005, 25(2): 103-107. LUO Ai-min, ZHANG Qi, LI Jian-ping, et al. Computational analysis of dispersion process of explosively driven solid fuel[J]. Journal of Beijing Institute of Technology, 2005, 25(2): 103-107. |
| [4] |
惠君明. FAE燃料抛散与云雾状态的控制[J].
火炸药学报, 1999, 22(1): 10-13. HUI Jun-ming. FAE fuel throw and control of cloud state[J]. Chinese Journal of Explosives & Propellants, 1999, 22(1): 10-13. |
| [5] |
赵海鸥.
LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社, 2003: 146-158.
|
| [6] |
王飞, 白春华, 闫华. 壳体厚度对大口径FAE战斗部效应仿真研究[J].
弹箭与制导学报, 2003, 28(3): 110-112. WANG Fei, BAI Chun-hua, YAN Hua. The study for the effect of the thickness of cylindrical shell on the fuel dispersing in the FAE warhead design by simulation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2003, 28(3): 110-112. |
| [7] |
LSTC inc. LS-DYNA keyword user′s manual (Nonlinear dynamic analysis of structures, Version 960)[CP], May 2001.
|
| [8] |
辛春亮, 秦健, 徐更光, 等. 基于LS-DYNA软件的水下爆炸数值模拟研究[J].
弹箭与制导学报, 2007, 28(3): 156-158. XIN Chun-liang, QIN Jian, XU Geng-guang, et al. Research on UNDEX numerical simulation based on LS-DYNA[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 28(3): 156-158. |
| [9] |
张奇, 白春华, 刘庆明, 等. 壳体对燃料近区抛散速度的影响[J].
应用力学学报, 2000, 17(3): 102 ZHANG Qi, BAI Chun-hua, LIU Qing-ming, et al. Influence of shell casting on fuel near-field dispersal velocity[J]. Chinese Journal of Applied Mechanics, 2000, 17(3): 102 |
| [10] |
Charles L. Mader. Numerical modeling of explosives and propellants (Second edition)[M]. CRC Press LLC, 1998.
|
| [11] |
张宝平, 张庆明, 黄风雷.
爆轰物理学[M]. 北京: 兵器工业出版社, 2001: 104-110.
|
The disperal velocity, explosive cavity and temperature of the fuel air explosive(FAE) devices with different center explosive charges were studied.




