熔铸类炸药在凝固过程中极易出现疏松、缩孔及微裂纹等,严重影响其成型质量[1], 为解决此类问题, 改善凝固工艺或对工艺参量的选取提供参照, 需要掌握炸药凝固过程中各类物理参量[2](如相流、传热、相变等)的变化信息。关于此类参量的实验监测和数值计算在国内外都已展开, 对炸药凝固温度场的研究, 通常采用热电偶法[2-6]监测, 有限元法[2, 4-7]、有限差分法[8]和控制容积法[3, 9]数值求解; 对相变及其界面的位置, 实验中用锥束CT扫描[1, 2]和超声透射[10]监测, 数值方法中用热焓法[3]或达西定律[9]来描述固/液相转变过程, 用线性插值法[11]确定相界面位置; 至于流场, 主要采用基于动量模型的数值方法[3, 9]研究等。上述方法的一些不足之处:热电偶法测温精度低、安全性差; 仅用传热偏微分方程描述炸药凝固的数值模型未考虑到液相流动对凝固进程及其它参量的影响; 以上研究对象几乎都是TNT基炸药, 对于以其它载体为基的熔铸炸药(如DNAN等), 有少量文献[12-16]报道其成型后的理化、爆轰性能和熔铸工艺概述, 但尚未有人对其凝固过程进行相关的实验监测, 以及从传热学和流动学角度出发, 用数值模拟方法对其凝固成型规律和机理进行深入的研究、分析。
2, 4-二硝基苯甲醚(DNAN)是一种可取代TNT的、极具发展前景的熔铸载体炸药[12-14, 16], 且DNAN基炸药(如PAX系列)已用于装填武器。本研究则用精度高、安全性好、多点分布式的Bragg光栅对DNAN炸药凝固过程的温度场进行了实时监测, 并结合控制容积法(考虑了液相的自然对流)对其凝固过程的一些物理参量(温度场、流场、相界面位置)进行了数值计算, 用临界固相率和补缩距离结合法预测了成型质量参量(缩孔)的生成特征, 并分析了各参量的递变规律及相互作用机理, 为此类炸药凝固工艺的改进和质量控制提供基本的物理依据。
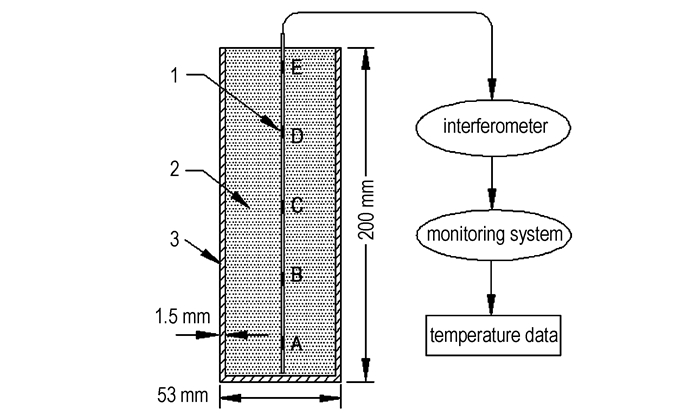
2 DNAN炸药凝固成型实验 2.1 实验装置FBG-3000型干涉解调仪, 实现Bragg光栅波长和物理量的测量; 多点分布式Bragg光栅组, 温度传感器, 其测温精度可达0.001 ℃, 5个光栅点A、B、C、D和E点的分布间距依次为40,50,50,40 mm, 实验前对每个光栅进行标定; 铝质模具:外径53 mm,内径50 mm,高200 mm, 模具壁和底厚1.5 mm; 监控系统, 包括FS-3000配置软件和显示器, 实现数据的采集和处理、显示与监控; W205C型恒温油浴锅, 用于熔化炸药; 测试对象为DNAN炸药。实验装置见图 1。
|
图 1 炸药凝固成型实验装置 1—布拉格光栅, 2—DNAN, 3—铝质模具 Fig.1 Experimental device for solidification of explosive 1— Bragg grating, 2—DNAN, 3—aluminum mould |
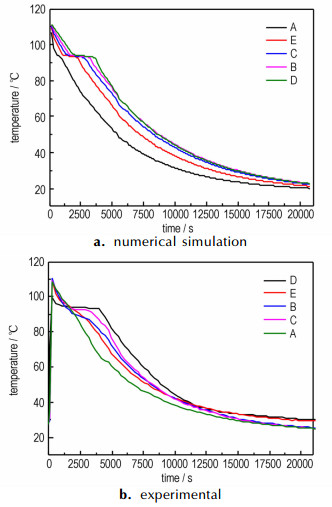
实验前固定光栅组于模具轴心处, 用W205C型恒温油浴锅缓慢加热DNAN炸药至110 ℃, 待完全熔化后注入模具, 事先启动配置软件, 在浇铸时开始测温(保存数据), 温度数据采集时间间隔为260 s, 待炸药冷却至常温(约25 ℃)时停止实验。用所测得的5组温度数据对时间作曲线见图 2b。
|
图 2 数值计算与实测的温度曲线 Fig.2 Temperature vs time of simulation and experiment |
为方便计算, 可参照文献[11]对炸药的物性和凝固特性做如下假设: (1)液态炸药为不可压缩流体, 动量方程计算中除外; (2)液相和固相为各向同性; (3)忽略晶粒的重熔; (4)导热系数是温度的单值函数。因此可用以下控制方程[3]描述DNAN炸药的凝固过程:
连续性方程:
| $ \rho \nabla \overrightarrow u = 0 $ | (1) |
动量方程:
| $ \frac{{\partial \left( {\mathop {\rho u}\limits^ \rightharpoonup } \right)}}{{\partial t}} + \nabla \left( {\overrightarrow {\rho u} \overrightarrow u } \right) = - \nabla \rho + \nabla \left( {\mu \nabla \overrightarrow u } \right) + \rho g\left[{1-\beta \left( {T-{T_{\rm{ref}}}} \right)} \right] + \mathit{S} $ | (2) |
能量方程:
| $ \rho \left( {{c_{\rm{p}}} + \frac{{\partial {f_1}}}{{\partial T}}\Delta H} \right)\frac{{\partial T}}{{\partial t}} + \nabla \left( {\rho {c_{\rm{p}}}\overrightarrow u T} \right) = \nabla \left( {k\nabla T} \right) $ | (3) |
| $ \Delta H = {f_l}L $ | (4) |
| $ \rho = \varepsilon (T) $ | (5) |
式中, ρ为密度,kg·m-3;
fl=1, T>Tl(液相点);
fl=0, T<Ts(固相点);
| $ {f_l} = (T - {T_{\rm{s}}})/({T_{\rm{l}}} - {T_{\rm{s}}}), {T_{\rm{s}}} < T < {T_{\rm{l}}} $ | (6) |
模拟的对象是圆柱状凝固系统, 模具内充填DNAN炸药。因其结构具有旋转对称性, 故取旋转对称面为53 mm×200 mm的矩形区域进行二维数值计算, 用前处理软件Gambit 2.4建模和划分四边形网格单元。
计算所用模具和炸药的物性参数[2, 14-16]:模具导热系数为240 W·m-1·℃-1, 比热0.9 kJ·kg-1·℃-1; DNAN密度表达式: (1.467-10-3T)kg·m-3, 粘度表达式: [exp(3.9+3130/T+8.5×105/T)]Pa·s, 潜热63.4 kJ·kg-1, 比热1.106 kJ·kg-1·℃-1, 固相点94.5 ℃, 液相点96 ℃, 导热系数:在Material studio 6.0软件的量子力学模块Castep下, 用加强热流法[17]求得DNAN导热项为0.226 W·m-1·℃-1, 其cif文件取自CCDC剑桥晶体结构数据库; 换热系数:模具与空气10 W·m-2·℃-1, 炸药与空气1 W·m-2·℃-1, 炸药同模具的换热采用流-固耦合算法[3], 液相初始温度110 ℃, 环境温度为25 ℃。
3.3 求解设定将Gambit输出的网格文件导入Fluent2D求解器(压力基), 在材料面板输入DNAN炸药和模具的性能参数并分配给各求解区域, 指定重力加速度沿Y轴负向, 设定模具、炸药自由面同空气为第三类热边界条件(换热系数和环境温度已知), 炸药同模具的换热采用流-固耦合算法。激活能量方程, 采用Solidification & Melting模型, 非稳态二阶显式格式, 迭代求解采用有限容积法[3, 11], 压力和速度的耦合采用SIMPLE算法[3, 11], 为加快收敛速度, 用Presto格式和二阶迎风格式离散压力项、速度项和能量项[11], 并对三者的亚松弛因子进行修正。在开始求解前, 用Patch面板初始化温度为110 ℃(炸药浇铸完毕后的初始温度), 迭代步数为20000步, 数据输出间隔时间100 s, 激活能量残差显示面板以观察迭代过程的收敛程度。
将同样的网格文件导入Procast前处理模块, 设置两种材料的性能参数、边界和初始条件。因DNAN粘度较TNT相当[15], 故近似采用TNT缩孔预测模型[6], 在运行参数面板中, 一、二次临界固相率(PIPES、MACROFS)分别取0.3和0.7, 补缩距离(FEEDLEN)取5 mm。
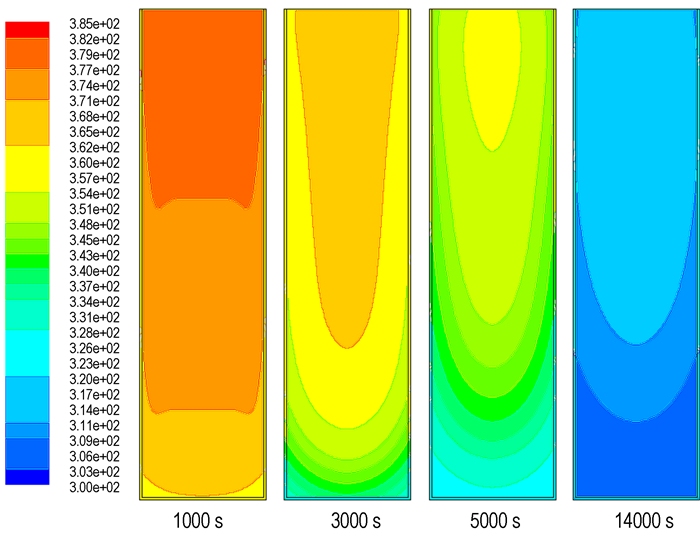
4 计算结果及分析 4.1 温度场图 2a是计算所得A~E点的温度曲线图, 图 2b为相应的实验测试结果, 图 3为不同时刻等温面的分布情况。
|
图 3 不同时刻的等温面分布图 Fig.3 Isothermal surfaces at different time |
从图 2可见两组曲线的走势大体相同, 说明模拟计算是较成功的。两组曲线变化的总趋势为渐减式递减, 但各点在96 ℃附近出现不同程度的等温平台, 其形成的原因: DNAN在温度区间(94.5~96 ℃)内发生相变, 释放结晶潜热[12]; 炸药凝固过程中各点的散热情况不同。据图 3和图 2b中可知此五点的凝固和降温顺序大致为A、E、B~D(E点位于形成缩孔的最上端, 受空气对流影响散热较B~D快), 且D处的潜热积累现象最明显, 为3000 s。图 2a、图 2b两组曲线的纵截距随位置高度的下降而增加, 随时间推进而减小, 图 3中的等温面亦可反映出来, 这是由于凝固顺序(图 5)的不同和温度(传热驱动力)下降所致。另外, 在前期液相较强的自然对流(近壁处达10-3量级)影响下, 等温面中心上凸且边缘下凹, 见图 3中1000 s时的分布。

|
图 5 相界面位置变化图 Fig.5 Change of interface positions |
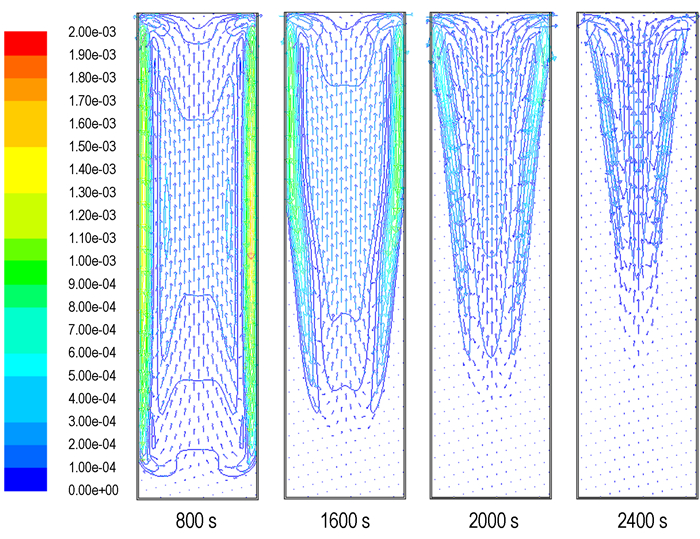
图 4给出的是凝固前期不同时刻炸药内部液相流动的速度矢量(箭头)、速度等值面(曲线)的分布情况, 左侧为矢量的大小。
|
图 4 不同时刻的速度矢量和等值面分布图 Fig.4 Velocity vector and isosurface at different time |
在凝固初始阶段, 靠近铸模的熔体往外传热较快, 密度增大并沿模壁向下沉积, 内层熔体受浮力驱动作用向上流动, 引起了液相部分的自然对流[3, 11], 此时的对流为纵向分布的整体环流, 从图 4可见, 初期800 s时外层液相的最大下沉速度最大可达0.00187 m·s-1且梯度较大。随着凝固和传质运输过程的发展, 冷流不断往下沉积形成固相, 外层熔体的流动方向由垂直方向逐渐往内侧倾斜、顶部回缩, 自然对流发展为局部环流, 其原因:液相内部上下温度差异引起密度分层; 液相温度下降时粘度增加, 流动性减弱; 液相部分靠近凝固前沿的堆积作用, 故局部环流的传输效果与前期整体环流相比大大降低。在后期, 液相平均温度与凝固点的温差缩小, 熔体层流速度减小, 在2400 s时最大流动速度为0.0004 m·s-1, 等值面分布稀疏, 此时导热成为驱动凝固进程的主要因素[11]。
4.3 相界面位置不同时刻相界面的位置可在求出每个时间步的温度分布后, 按线性假设对单元内温度值进行插值[11], 对于相变单元任意一边, 若(Ti-T0)(Ti+1-T0)<0, 则Ti、Ti+1间存在相变点, 坐标如下:
| $ \begin{gathered} x = ({f_{l}}\cdot{x_{i + 1}} + {x_i})/(1 + {f_l}); \hfill \\y = {y_i} \hfill \\ \end{gathered} $ | (7) |
式中, Ti、Ti+1为连续时间步所得温度, T0为线性假设发求得的单元内温度插值, fl为液相率。
图 5是用温度插值法计算出的DNAN炸药凝固过程不同时刻的相界面位置, 左侧为液相率。
分析图 2~图 5可知, 在炸药凝固过程中, 边界换热和自然对流是影响凝固速度、相界面位置变化的主要因素。在前期, 由于铸模边界处的快速换热、熔体密度分层[3, 11](重力所致)两方面的共同作用下, 凝固首先从模具底部进行, 相界面大致呈平行层向上推进, 且因固相层厚度小, 热流速率较高, 凝固相前沿的糊状区域(Mushy zone)面积狭小。随着自然对流过程的进行, 靠模具壁处冷流下沉和固相堆积速率均较中心位置高, 且边界处熔体的快速散热亦加速了凝固进程, 致使相界面呈内凹的“V”型并向上推移、回缩。由于下方固相层厚度大、热传导速率小, 糊状区域面积扩大, 且在垂直方向分层明显。在顶部, 液相同环境空气的对流换热所形成的凝固壳与下方的固相形成封闭区域, 液相最终消失于此封闭区内。
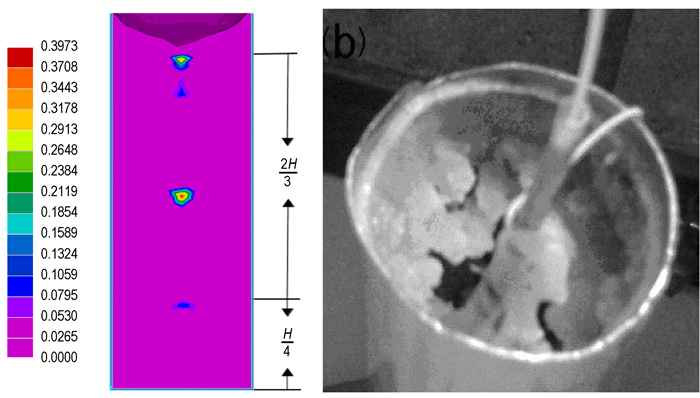
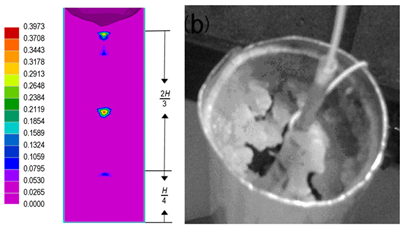
4.4 缩孔预测用临界固相率和补缩距离结合法[2, 5-7]对DNAN凝固后的缩孔缩松进行预测, PIPES和MACROFS分别取0.3和0.7, FEEDLEN取5 mm。其结果见图 6, 图 6a为孔隙率, 图 6b为实验结果。
|
图 6 缩孔生成的预测和实验观测 Fig.6 Prediction and experimental results of shrinkage hole |
从图 6a可看出DNAN凝固结束后, 在H/4至11H/12的轴心位置分布有大面积的二次缩孔, 其中H/2处最为明显, 最大孔隙可达0.38, 这与文献[2, 6]中无冒口补缩的实验结果基本一致, 另外图 6a中自由表面下陷形成的一次缩孔[6]对应着图 6b中上表面的凹陷区域, 因实验中传感器为液相的结晶提供形核面, 析出的晶粒在其表面聚集而导致内部缩孔显露出来, 与预测结果略有不同。结合图 5和图 6可知缩孔形成的主要原因:下部的凝固层首先形成且生长速度大于径向, 致使糊状区逐渐呈狭长“V”型纵向分布, 但模型尺寸长宽比较大, 当V型区域的固相率大于缩孔生成的临界固相值, 且补缩距离大于临界值时, 上层熔体不再下移, 形成了二次缩孔; 凝固收缩(因密度变化), 固、液相收缩[2](温度引发热膨胀量的变化), 都会导致DNAN炸药体积的收缩, 且凝固装置无冒口给予熔体补偿, 故在自由表面生成一次缩孔。
5 结论(1) 用控制容积法对DNAN凝固过程进行了数值计算, 其中DNAN凝固成型实验的中心轴线温度场与数值计算结果基本一致。
(2) 在自然冷却、铝质模具、柱体截面为Φ50 mm×200 mm容积的成型条件下, DNAN降温至96 ℃附近时出现温度滞后现象, 愈靠中心位置愈明显, 最大滞后时间为3000 s。液相自然对流的最大流速可达0.00187 m·s-1, 在凝固初期起运输和加速凝固进程的作用, 自然对流和边界换热使相界面呈“V”型上移、收缩。
(3) DNAN炸药凝固结束后, 从H/4至11H/12处有连续的缩孔出现, 其中在H/2处最为明显, 最大孔隙率为0.38。
本研究可为DNAN及以其为液相载体的混合炸药凝固成型机理及工艺参数优化的确定、方案的改进提供基础理论依据。
| [1] |
田勇, 刘石, 张伟斌, 等. TNT炸药熔铸结晶成型过程μCT实验研究[J].
含能材料, 2009, 17(2): 173-176. TIAN Yong, LIU Shi, ZHANG Wei-bin, et al. Experimental study on crystallization of casting TNT explosive during solidification by high-resolution X-ray CT[J]. Chinese Journal of Energetic Materials, 2009, 17(2): 173-176. |
| [2] |
田勇. 炸药熔铸过程监测评价及数值模拟研究[D]. 中国科学院研究生院, 绵阳, 2010.
TIAN Yong. Process monitoring/evaluation and numerical simulation during casting explosive solidification[D]. Mianyang: Graduate University of Academy of Sciences, 2010. |
| [3] |
Dawei S, Suresh V G. Numerical and experimental investigation of the melt casting of explosives[J].
Prop Expl Pyro, 2005, 5: 30 |
| [4] |
Mudryy R, Sanjeev S. Modeling and simulation of melt cast explosives[C]//Insensitive Munitions and Energetic Materials Technology Symposium. Arlington 2007.
|
| [5] |
黄勇, 郑保辉, 谢志毅, 等. 熔铸炸药加压凝固过程研究[J].
含能材料, 2013, 21(1): 25-29. HUANG Yong, ZENG Bao-hui, XIE Zhi-yi, et al. Pressured solidification process of melt-cast explosive[J]. Chinese Journal of Energetic Material(Hanneng Cailiao), 2013, 21(1): 25-29. |
| [6] |
李敬明, 田勇, 张伟斌, 等. 炸药熔铸过程缩孔和缩松的形成与预测[J].
火炸药学报, 2011, 34(2): 17-20. LI Jing-ming, TIAN Yong, ZHANG Wei-bin, et al. Formation and prediction of shrinkage hole and shrinkage porosity in explosive during casting process[J]. Chinese Journal of Explosives and Propellants, 2011, 34(2): 17-20. |
| [7] |
WANG Dong-lei, XIE Zhi-yi, HUANG Yong, et al. Solidification simulation material of melt-cast explosive under pressurization[C]//Material Science Forum, 2011, 704-705.
|
| [8] |
CHEN Chun-yu, SHIUAN Jonq-hwa. Numerical simulation of casting explosives in shell[J].
Prop Expl Pyro, 1992, 17: 20-26. DOI:10.1002/(ISSN)1521-4087 |
| [9] |
JI Ching-china, LIN Ching-show. The solidification process of melt casting explosives in shell[J].
Prop Expl Pyro, 1998, 23: 137-141. DOI:10.1002/(ISSN)1521-4087 |
| [10] |
ZHANG Wei-bin, TIAN Yong, ZHOU Hong-ping, et al. Process monitoring of cast explosive solidification molding by on-line multichannel ultrasonic measurement [C]//17th World Conference on Nondestructive Testing, Shanghai, 2008, China.
|
| [11] |
柴美厚, 曾丹苓, 张志荣. 自然对流下的凝固过程数值模拟[J].
重庆大学学报(自然科学版), 2005, 28(6): 37-40. CHAI Mei-hou, ZENG Dan-ling, ZHANG Zhi-rong. Numerical simulation of the solidification process under the effect of nature convection[J]. Journal of Chongqing University (Natural Science Edition), 2005, 28(6): 37-40. |
| [12] |
Phil J D, Arthur P. Characterization of 2, 4-dinitroanisole: an ingredient for use in low sensitivity melt cast formulations[R]. Defense Science and Technology Organization (Australian), DSTO-TR-1904.
|
| [13] |
王春光, 魏敏, 刘学柱, 等. DNAN基高威力钝感熔铸炸药装药工艺应用[J].
兵工自动化, 2013, 32(1): 42-45. WANG Chun-guang, WEI Min, LIU Xue-zhu, et al. Charging technology application of high power insensitive melt-pour explosive based on DNAN[J]. Ordnance Industry Automation, 2013, 32(1): 42-45. DOI:10.7690/bgzdh.2013.01.013 |
| [14] |
XING Xiao-ling, ZHAO Feng-qi, MA Shun-nian, et al. Specific heat capacity, thermal behavior, and thermal hazard of 2, 4-dinitroanisole[J].
Prop Expl Pyro, 2012, 37: 179-182. DOI:10.1002/prep.v37.2 |
| [15] |
Donald W M, Lohr A B, William S M. Viscosity and density of the liquid system TNT-picric acid and four related pure materials[J].
J Chem Phys, 1956, 25(6): 1235-1240. DOI:10.1063/1.1743185 |
| [16] |
邵颖惠, 任晓宁, 刘子如, 等. 2, 4-二硝基苯甲醚熔体及其在介质中的非等温结晶[J].
化学分析计量, 2011, 20(增刊): 22-25. SHAO Ying-hui, REN Xiao-ning, LIU Zi-ru, et al. DNAN and its non-isothermal crystallizations in RDX and in AP[J]. Chemical Analysis and Meterage, 2011, 20(zl): 22-25. |
| [17] |
饶中浩, 汪双风, 张艳来, 等. 相变材料热物理性质的分子动力学模拟[J].
物理学报, 2013, 62(5): 056601 RAO Zhong-hao, WANG Shuang-feng, ZHANG Yan-lai, et al. Molecular dynamics simulation of the thermophysical properties of phase change material[J]. Acta Phys Sin, 2013, 62(5): 056601 |
The temperature field in the central axis in the solidification process of DNAN was tested by Bragg gratings. The microscopic phenomenon of natural convection of liquid phase was considered. The temperature field, flow field and phase interface position for the solidification process of DNAN were calculated by volume-control method. The formation of shrinkage holes and shrinkage porosities were predicted by considering both critical solid phase fraction and feeding length.




