多年来,国内外采用12型、12B型、卡斯特落锤仪等装置测定炸药固体颗粒的撞击感度,通过颜色变化、气味、冒烟、声响等综合判断试样是否发生点火,并且采用爆炸概率或特性落高等形式评价炸药的撞击感度。目前,一些国外学者[1]从分子动力学角度利用ReaxFF(reactive force field)反应力场研究了RDX和HMX在高速(8.6 km·s-1)冲击下的撞击响应特性,并比较了不同晶形炸药的撞击感度大小,数值模拟结果与实际相符,开辟了一条新的炸药撞击响应研究途径;国内学者周培毅等[2]对炸药装药在后座冲击载荷下的动态响应进行了数值计算,但只考虑了底隙中留存的空气在后座冲击下绝热压缩致高温和炸药塑性变形能引起的温升,而没有考虑炸药本身的分解反应放热;李凯等[3]基于Johnson-Cook本构模型,对点火前的Comp.B炸药大落锤(400 kg)冲击实验进行了数值模拟,研究了Comp.B炸药在惯性冲击下的力学响应特性,而对冲击下的炸药点火特性未考虑。撞击感度测试装置中落锤的惯性冲击不同于一般的冲击载荷,其强度较低(<1 GPa),持续时间较长(约几毫秒),炸药在标准撞击感度仪的落锤自由落体撞击下产生热力耦合作用且考虑炸药本身分解放热反应的点火数值模拟研究至今还未见报道。
为此,本研究基于热力耦合模型,利用大型有限元分析软件ANSYS/LS_DYNA对典型混合炸药Comp.B炸药的撞击感度实验进行了数值模拟,探讨Comp.B炸药在落锤撞击响应下考虑炸药本身放热反应的宏观热力耦合模型的点火可行性,其计算结果可为判断炸药撞击点火提供理论依据。
2 炸药撞击感度实验仪器炸药撞击响应过程是非线性的且远离平衡态的热力学过程。在撞击作用下,炸药晶体间或晶体与撞击仪器间的相对运动非常复杂。这种运动会在炸药晶体间形成一定的高应力,出现与塑性材料受压相似的塑性变形,炸药晶体间则形成强烈的摩擦、挤压、剪切,导致强烈的局部生热,出现温度相当高的热点或者热点群源[4]。此外在这种高应力作用下,炸药的反应速率即其反应能力就起着重要作用。图 1是标准撞击仪器结构图。上下击柱、导向套及底座都是钢质材料,击柱尺寸为Φ10 mm×10 mm,导向套尺寸外径Φ40 mm,内径Φ10 mm,高16 mm,底座尺寸外径Φ50 mm,内径Φ40 mm,高25 mm。炸药置于上下击柱及导向套中间。实验中,落锤从一定高度自由落体后撞击上击柱,上击柱以一定速度冲击炸药,炸药在相对密闭空间受挤压、塑性变形、摩擦及剪切等发生爆炸现象。

|
图 1 标准撞击仪器结构图 1—上、下击柱,2—导向套,3—底座,4—炸药 Fig.1 Schematic diagram of impact apparatus 1—impact plunger, 2—guide sleeve, 3—base, 4—explosive |
对撞击感度仪及药片进行三维实体建模并采用三维热分析单元solid164对该模型进行网格划分。为了减少计算量,根据撞击感度实验所用击柱、导向套、底座等器材进行简化建模,分别对击柱及导向套的实际尺寸减小,同时也不影响计算结果。因此,有限元模型的上击柱高4 mm,下击柱高1 mm,50 mg药柱高约2 mm,钢导向套壁厚1 mm,高4 mm。因为下击柱可以通过设置节点组约束固定不动,所以底座可以省略不用建模。由于整个模型对称,故建立四分之一有限元模型,如图 2~图 6所示。

|
图 2 上击柱 Fig.2 Up impact plunger |
|
图 3 下击柱 Fig.3 Down impact plunger |

|
图 4 炸药片 Fig.4 Explosive piece |
|
图 5 导向套 Fig.5 Guide sleeve |
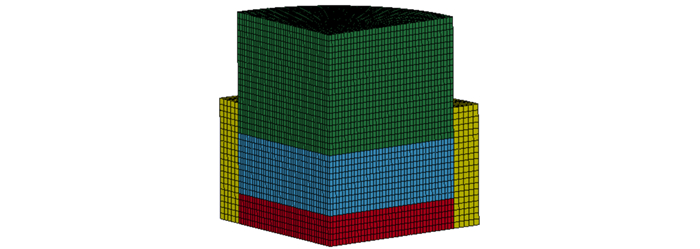
|
图 6 有限元模型组合图 Fig.6 Integral sketch of finite element model |
对炸药片的撞击过程进行瞬态生热和热力耦合作用分析时,启用关键字CONTROL_SOLUTION,其中SOLN的参数取值2,即可进行热力耦合分析。另外,对有限元模型及计算方法进行了一定的简化处理。
(1) 放置在击柱与导向套之间的测试药量大约为30~50 mg,测试前轻轻挤压旋转上击柱使散状炸药颗粒较均匀地分布在击柱与导向套之间,认为形成了一定厚度的均匀炸药薄片。
(2) 由于药片在撞击作用下发生放热反应极快(约几毫秒),则药片和击柱、导向套的热传导效果忽略不计。
(3) 药片无辐射散热,撞击过程中产生的热量全部用于药片温升。
(4) 药片导热过程仅与时间有关,不考虑温升等因素导致的材料导热系数变化的影响。
(5) 落锤撞击实验传感器测到的撞击时间数量级是10-3 s[5],因此认为炸药片产生热点并发生爆炸的时间在1 ms以内。
3.2 边界条件根据击柱和药片撞击接触的情况,除考虑了药片在外界作用力挤压、剪切等产生的塑性变形能外,药片本身发生爆炸释放热量的过程采用在药片单元上加载生热率载荷,生热速率采用LOAD_HEAT_GENERATION_SET关键字加载,模拟炸药发生剧烈的化学反应。药片内部热量的传导通过定义热传导系数完成加载。
整个撞击仪器及药片的初始温度为20 ℃,用关键字INITIAL_TEMPERATURE_SET设置。用关键字BOUNDARY_TEMPERATURE_SET设置热边界条件温度,上下击柱、导向套及底座的热边界条件温度为20 ℃。
3.3 材料模型及参数击柱和导向套的材料均为钢质,材料模型采用MAT_ELASTIC,其材料参数见表 1。
| 表 1 钢材料参数 Tab.1 Parameters of steel |
炸药片材料采用关键字为MAT_ELASTIC_VISCOPLASTIC_THERMAL控制的带热效应的弹性-粘塑性材料模型。
本文以Comp.B炸药(TNT/RDX/WAX, 59.5/39.5/1[6])为例,其力学性能见表 2。
| 表 2 Comp.B炸药在高应变率下的力学参数[5] Tab.2 Mechanical parameters of Comp.B explosive subjected to high strain rate |
T=20 ℃时,从文献[7]中Comp.B的应力-应变曲线上采取各个关键点得到表 3。
由于TNT的比热Cp1=1370 J·kg-1·℃-1,RDX的比热Cp2=1130 J·kg-1·℃-1,则Comp.B炸药的比热为Cp=1274 J·kg-1·℃-1。Comp.B炸药的热物性参数见表 4。
| 表 4 Comp.B炸药的热物性参数 Tab.4 Thermal parameters of Comp.B explosive |
当上下击柱、导向套与药片接触时,必须考虑热接触的问题才能计算。对于三维热接触,使用CONTACT_SURFACE_TO_SURFACE_THERMAL_TITLE关键字进行定义。但是在进行热力耦合分析时对模型进行了简化处理,不考虑击柱、导向套和药片之间的热传导,故该热接触关键字的热传导系数设置非常小,认为近似不会热传导。
4 计算结果及分析当落锤撞击速度不同时,药柱材料升温速率及拐点温度呈现规律性变化,下面就不同速度下炸药片温度上升及热点分布情况进行模拟计算。
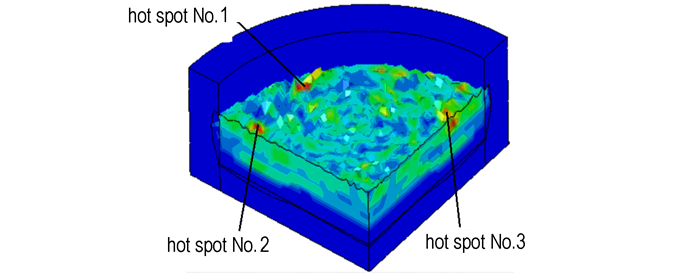
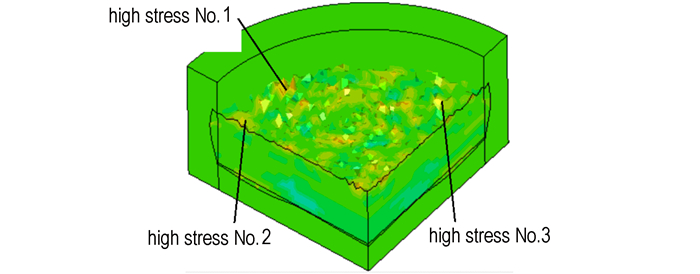
图 7和8分别是药片在一定速度撞击下的热点和应力分布图。图 7中热点单元1, 2, 3分别对应着图 8的高应力单元1, 2, 3,说明在外界机械作用撞击下,由于挤压、剪切等作用导致药片局部产生高应力,从而在相应高应力区域出现热点。数值模拟结果与炸药撞击感度作用过程的理论分析、实验观测结果一致,说明应用热力耦合模型的计算方法具有可行性,计算结果具有一定可信度。
|
图 7 炸药片热点分布图 Fig.7 Hot-spot distribution of explosive piece |
|
图 8 药片应力分布图 Fig.8 Stress distribution of explosive piece |
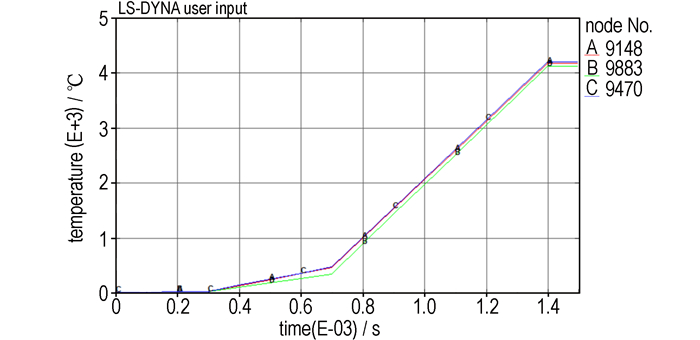
当落锤撞击上击柱时,如果上击柱产生的速度为v=5 m·s-1时,则药柱的拐点温度为476.5 ℃。炸药单元大约在0.7 ms时刻出现温度拐点(图 9),由初始的逐渐缓慢升温过程突然转变为急剧升温。一般认为,炸药热点形成后的温度范围在300~600 ℃之间。根据文献[5]可知,假定临界爆炸延滞期按10-5 s计算,则可得到Comp.B炸药的临界热点温度为417 ℃,因此可以认为0.7 ms时炸药内部开始形成热点并发生点火反应。
|
图 9 节点温度上升及拐点图 Fig.9 Rising temperature curves and inflection point of nodes |
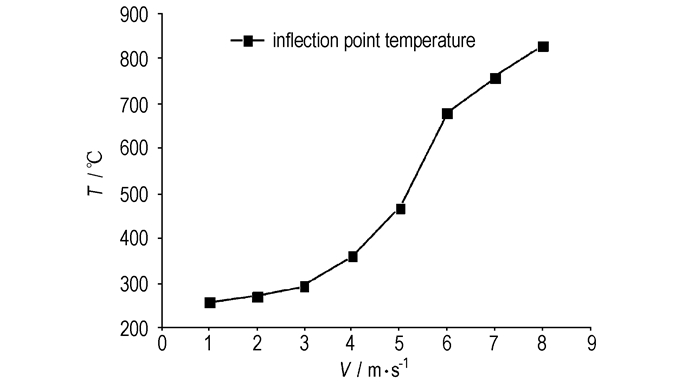
图 10是在落锤撞击下导致击柱产生不同速度时Comp.B炸药片的温度拐点变化曲线。
|
图 10 温度拐点变化曲线 Fig.10 Temperature inflection point change curve |
由图 10可知,随着上击柱速度的增加,炸药片的温度拐点逐渐增大,低速阶段增加缓慢,当速度v=4.5 m·s-1时,炸药内部热点温度约为417 ℃,处于临界点火状态;当速度v=5 m·s-1时拐点温度急剧增大,由此说明上击柱速度大于v=5 m·s-1时,炸药内部的热点容易形成并发生点火的概率大大增加。此外,根据文献[8]可知,Comp.B炸药撞击感度的特性落高为109 cm(采用LANL12型B仪器,2.5 kg落锤)。假设落锤的全部势能转化为动能,则由击柱速度可计算落锤的高度,当击柱速度分别为4.5、4.6、4.7、4.8、4.9和5 m·s-1时,对应的落锤高度各自为103、108、113、117和127 cm。因此,当击柱速度v=4.6 m·s-1时,Comp.B炸药撞击感度数值模拟计算结果与实际特性落高吻合良好。
5 结论利用大型有限元软件ANSYS/LS_DYNA中带热效应的弹性-粘塑性材料模型,采用热力耦合计算方法,考虑炸药自身的化学放热反应,以生热速率(W·m-3)来衡量,用LOAD_HEAT_GENERATION_SET关键字加载,模拟炸药发生剧烈的化学放热反应。数值模拟过程表明,该方法对模拟炸药瞬态放热并在内部产生急剧温升的效果非常显著,具有可行性。同时,考察了不同击柱速度下炸药内部热点的形成过程及变化规律。计算结果显示,随着击柱速度的增大,炸药内部的高温热点越容易形成。当击柱v=4.6 m·s-1时数值模拟计算的Comp.B炸药特性落高与文献值吻合良好,并在击柱速度v=5 m·s-1时热点温度急剧增大,发生爆炸的概率大大增加,其中, 算例Comp.B炸药在0.7 ms时炸药内部开始形成接近或超过临界温度的热点并发生点火反应。此外,随着击柱速度的增大,炸药内部的整体温度也急剧增大,更有利于炸药的热点形成并易发生爆炸。
炸药落锤撞击点火数值模拟研究为探讨炸药在外界机械作用下的内部热点形成规律以及宏观点火特性提供了一种新思路和解决方法,并且该计算结果为判断炸药撞击是否点火提供了理论依据。
| [1] |
ZHANG Lu-zheng, Zybin Sergey V, Duin Adri C T Van, et al. Modeling high rate impact sensitivity of perfect RDX and HMX crystals by ReaxFF reactive dynamics[J].
Journal of Energetic Materials, 2010, 28(Suppl 1): 92-127. |
| [2] |
周培毅, 徐更光, 王廷增. 炸药装药在后座冲击条件下的点火模型研究[J].
火炸药学报, 2000(1): 1-5. ZHOU Pei-yi, XU Geng-guang, WANG Ting-zeng. Ignition models of explosive charge subjected to setback impact[J]. Chinese Journal of Explosives & Propellants, 2000(1): 1-5. |
| [3] |
李凯, 朱建生, 钱志博, 等. 基于J-C本构模型的Comp. B炸药落锤冲击数值模拟[J].
力学与实践, 2011, 33(1): 21-23. LI Kai, ZHU Jian-sheng, QIAN Zhi-bo, et al. Numerical simulation of drop weight impact tests for Comp. B using Johnson-Cook constitutive model[J]. Mechanics in Engineering, 2011, 33(1): 21-23. |
| [4] |
金韶华, 松全才.
炸药理论[M]. 西安: 西北工业大学出版社, 2011: 317-325.
|
| [5] |
赵省向, 张亦安. 几种熔铸炸药的热点临界参数和撞击感度[J].
含能材料, 2003, 11(3): 127-129. ZHAO Sheng-xiang, ZHANG Yi-an. The critical initiation parameters of hot-spots and impact sensitivity of melt-cast explosives[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2003, 11(3): 127-129. |
| [6] |
韩小平, 张元冲, 沈亚鹏. Comp. B复合炸药动态力学性能和塑性流动本构关系的研究[J].
力学学报, 1996, 28(3): 319-326. HAN Xiao-ping, ZHANG Yuan-chong, SHEN Ya-peng. A study of dynamic mechnical response and constitutive model of energetic materials[J]. Acta Mechanica Sinica, 1996, 28(3): 319-326. |
| [7] |
韩小平, 张元冲, 沈亚鹏. Comp. B复合炸药动态压缩力学性能和本构关系的研究[J].
实验力学, 1996, 11(3): 303-310. HAN Xiao-ping, ZHANG Yuan-chong, SHEN Ya-peng. Dynamic behavior and constitutive model of Comp. B explosive[J]. Journal of Experimental Mechanics, 1996, 11(3): 303-310. |
| [8] |
孙国祥.
混合炸药及其发展[M]. 西安: 中国兵器集团第二零四研究所, 2008: 18-19.
|
The ignition characteristics and the law of hot-spot formation on comp.B explosive subjected to drop weight impact have been investigated using nonlinear dynamics finite element software ANSYS/LS_DYNA. The finite element model used to simulate impact sensitivities was built using comp.B explosives as a caculation example. Information is obtained on the explosive impact ignition.




