含铝炸药作为典型的贫氧炸药,具有高爆热和高比容的特点,广泛用于对空武器弹药及水下武器弹药中[1]。通常情况下,贫氧炸药在爆轰反应后,会形成大量的富含燃料的爆轰产物[2-3],影响了炸药总能量的释放。因此,为了增强贫氧炸药的爆炸能量输出,就要求其形成的大量的富含燃料的爆轰产物能够在爆轰反应区后,继续进行反应(即后燃反应),并对后燃反应释放的能量加以利用。对于贫氧炸药的后燃效应,目前已经逐步为人们所认识,但我国至今未能就此进行系统研究。
本研究设计使用了一种增强贫氧炸药后燃效应的双层容器试验装置,以钝黑铝(AⅨ-Ⅱ)、某含铝炸药(JAL)为研究对象,将其置于内层容器中,内外层容器间充填一定压力的氧气、空气等介质,用来增强炸药爆轰后的后燃效应。由于在开放空间测试贫氧炸药后燃效应的难度很大,本研究采用目前国内外较为精确测量炸药能量的方法—水下爆炸测试方法[4-5],对含铝炸药在不同压力下空气和氧气中的后燃效应进行了测试、计算和比较,试图能通过这种设计给出表征贫氧炸药后燃效应能量的方法。
2 实验实验中使用了两种主装药,分别是AⅨ-Ⅱ和JAL。AⅨ-Ⅱ和JAL均为圆柱形压装药,每发质量为200 g,直径40 mm,密度分别为1.74 g·cm-3和1.95 g·cm-3。AⅨ-Ⅱ成分为RDX 76%、Al 20%、蜡4%(质量分数),爆热为6.696 kJ·g-1,爆速为8.09 km·s-1(ρ=1.77 g·cm-3),氧平衡为-0.48,主要用于装填小口径炮弹[1]。JAL是以HMX为基的含铝炸药,爆热为8.6 kJ·g-1,氧平衡约为-0.357。起爆系统使用8号电雷管,为了使主装药爆轰完全,每发主装药均使用一个直径15 mm、密度为1.72 g·cm-3的JH-14[6]传爆药柱,质量为5 g。
为了充分表征贫氧炸药的后燃效应,设计了如图 1所示的一种增强贫氧炸药后燃效应的双层容器试验装置(以下简称试验装置)。进行水下爆炸测试时,被测炸药试样被置于该试验装置的内层圆筒形容器中并做好防水处理,在内、外层容器形成的封闭空腔内可以充填一定压力的气体。试验装置材料采用20号钢,环行部分采用无缝钢管加工,经计算,试验装置内充装气体的容积为6.024 dm3。实验时试验装置内分别充有空气(0.1,0.6,4.6 MPa)、氧气(0.6,1.0,4.6 MPa)和氮气(0.6,1.0,4.6 MPa),压力数值均为绝对压力。实验时每种实验情况均进行两发平行实验。
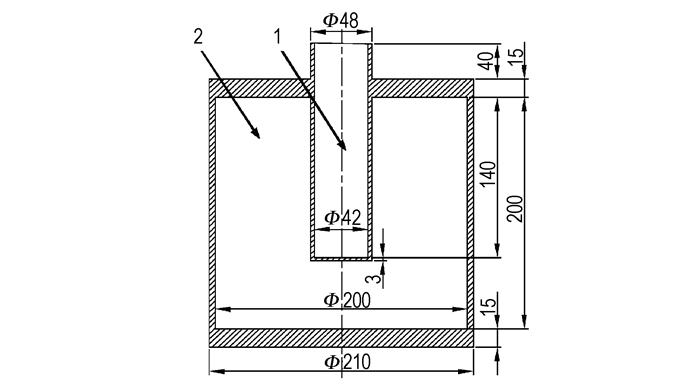
|
图 1 试验装置的尺寸图 1—内层容器, 2—外层容器 Fig.1 Dimensional sketch of test device 1—inner container, 2—outer container |
实验在Φ 8 m×8 m的刚性水池中进行,水池池壁与池底材质均为钢板。首先对距爆心同一距离、同一水平但不同方位处的水下爆炸参数进行测量,为此将两个传感器与试验装置布放在水面下4.25 m处,试验装置距池壁水平距离为3 m,两个传感器分别距试验装置2.5 m,且以实验装置为顶点、水平方向上夹角为45°,实验布置如图 2所示。其次,对水下爆炸相似律和后燃效应进行测量,此时试验装置和传感器仍布放在水面下4.25 m处,试验装置距池壁水平距离为3 m,4个传感器与试验装置处在爆炸水池同一直径上,距试验装置分别为2, 2.5, 3, 3.5 m,实验布置如图 3所示。测试时,通过实验记录水下固定位置上的压力时程曲线,使用了PCB138系列的ICP(internal circuit piezoelectric)电气石水下传感器、PCB482A16型信号调理仪、国产纵横公司JV5200数据采集仪及Jovian软件进行信号采集、存储和处理。
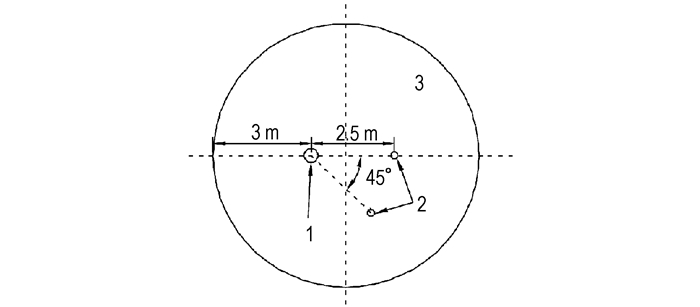
|
图 2 测量不同方位水下爆炸参数的实验布置示意图 1—试验装置, 2—传感器, 3—水池 Fig.2 Sketch of experimental disposal for measuring underwater explosion parameters in different directions 1—test device, 2—sensors, 3—water pool |
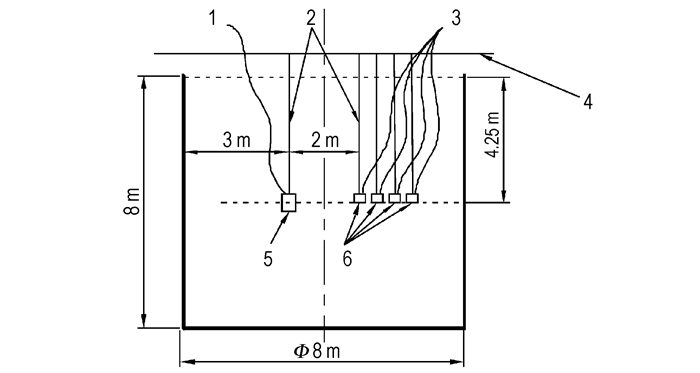
|
图 3 测量后燃效应的实验布置示意图 1—起爆电缆, 2—承重绳索, 3—传输电缆, 4—实验支架, 5—试验装置, 6—传感器 Fig.3 Sketch of experimental disposal for measuring afterburning effect 1—ignition cable, 2—load rope, 3—transmission cable, 4—experimental holder, 5—test device, 6—sensors |
根据水下爆炸相似律,当冲击波参数不进行修正时,爆源比冲击波能еs′的计算公式为[7]
| $ {{e}^{'}}_{\rm{s}}=\frac{4\rm{ }\!\!\pi\!\!\rm{ }{{R}^{2}}}{{{\rho }_{\rm{w}}}{{C}_{\rm{w}}}}\frac{1}{W}\int_{0}^{\tau }{p{{\left( t \right)}^{2}}\rm{d}}t $ | (1) |
式中,R为爆心至测点的距离,m; W为装药质量,kg; ρw为水的密度,kg·m-3,本文取1000 kg·m-3; Cw为水中音速,m·s-1,取1500 m·s-1; p(t)为测点处t时刻冲击波压力,Pa; τ为积分上限(由于冲击波压力时程曲线衰减较慢,本文取51.7 θ,此时冲击波压力已降至峰值压力的5%以下); θ为水中冲击波的衰减时间常数,取压力从峰值pm首次衰减到pm/e所需的时间间隔,μs。
考虑传感器几何形状对测量波形的影响,Jensen给出的修正方法为[8]:
| $ {{p}_{\rm{m}}}={{K}_{\rm{p}}}\cdot \rm{ }{{p}^{'}}_{\rm{m}} $ | (2) |
| $ {{e}_{\rm{s}}}={{K}_{\rm{e}}}\cdot \rm{ }{{e}^{'}}_{\rm{s}} $ | (3) |
式中,p′m为实测的冲击波峰压, MPa; e′s为实测的比冲击波能, kJ·g-1; pm为修正后的冲击波峰压, MPa; es为修正后的比冲击波能, kJ·g-1; Kp为冲击波峰压的修正系数; Ke为比冲击波能的修正系数。
Kp、Ke与压力传感器传感头的直径、冲击波的衰减时间常数和水中音速有关,即:
| $ {K_{\rm{p}}} = 1 + 0.5\gamma + 0.06{\gamma ^{1.6}} $ | (4) |
| $ {K_{\rm{e}}} = 1 + 0.29\gamma + 0.016{\gamma ^2} $ | (5) |
| $ \gamma {\rm{ = }}\frac{d}{{{C_{\rm{w}}} \cdot \theta }} $ | (6) |
式中,d为压力传感器传感头的直径,mm,本实验为6.35 mm; Cw为水中音速,mm·μs-1,取1.5 mm·μs-1; θ为水中冲击波的衰减时间常数,μs。
由此得出水中测点处比冲击波能修正后的计算公式为:
| $ {e_{\rm{s}}} = {K_{\rm{e}}}\frac{{4{\rm{ \mathit{ π} }}{R^2}}}{{{\rho _{\rm{w}}}{C_{\rm{w}}}}}\frac{1}{W}\int_0^\tau {p{{\left( t \right)}^2}{\rm{d}}} t $ | (7) |
由于有限水域水下爆炸存在边界效应使气泡脉动周期与药量之间关系稍偏离Willis公式,于是实际有限水域水下爆炸爆源的比气泡能eb的计算公式为[7]:
| $ {e_{\rm{b}}} = \frac{1}{{8{C^3}K_1^3W}}{\left[{\sqrt {1 + 4C{T_{\rm{b}}}}-1} \right]^3} $ | (8) |
式中,C、K1为与给定水池给定装药位置有关的常数,K1=1.135 ρw1/2/phn5/6,在本实验条件下,实测并以最小二乘法计算得到C=0.4147 s-1。Tb为将实测气泡脉动周期tb修正到同一大气压下的总流体静压phn下的气泡脉动周期,修正公式为:
| $ {T_{\rm{b}}} = {t_{\rm{b}}}{\left( {\frac{{{p_{{\rm{hi}}}}}}{{{p_{{\rm{hn}}}}}}} \right)^{5/6}} = {t_{\rm{b}}}{\left( {\frac{{{p_{\rm{i}}} + {p_{\rm{h}}}}}{{{p_0} + {p_{\rm{h}}}}}} \right)^{5/6}} $ | (9) |
式中,phi为装药深度处的总流体静压,Pa; pi为测试时水面实测大气压,Pa,每次实验根据天气有所变化; p0为水面标准大气压,取101325 Pa; ph为装药深度处的静水压力,Pa。
3.3 炸药总比能量的计算当冲击波的比冲击波能以及比气泡能求出以后,炸药的总比能量et为[8]:
| $ {e_{\rm{t}}} = {K_{\rm{f}}}\left( {\mu {e_{\rm{s}}} + {e_{\rm{b}}}} \right) $ | (10) |
式中,Kf为装药的几何形状系数,对于球形装药Kf=1,对于非球形装药Kf≥1; μ为冲击波衰减系数,是考虑测点距离对冲击波衰减的影响而采用的修正系数,仅与爆轰压pCJ(108 Pa)有关,计算式如下:
| $ \begin{array}{l} \mu = 1 + 1.3328 \times {10^{-2}}{p_{{\rm{CJ}}}}-6.5775 \times {10^{-5}}p_{{\rm{CJ}}}^2 + \\ \;\;\;\;\;\;\;1.2594 \times {10^{ - 7}}p_{{\rm{CJ}}}^3 \end{array} $ | (11) |
为了考察装药在试验装置作用后水下不同方位处的压力情况,对距装置同一距离、同一水平但不同方位的水下爆炸参数进行研究(见图 2)。选取JAL炸药在充装有1.0 MPa氧气的试验装置中的实验数据,列于表 1。由表 1可知,在实验误差范围内,可以认为距爆心同一距离不同方位处的水下爆炸参数一致。这也说明装置外壳体在爆炸过程中是各向均匀解体的。
| 表 1 不同方位水下爆炸参数 Tab.1 Underwater explosion parameters in different directions |
由于距试验装置同一距离不同方位处的水下爆炸参数相同,故只需在一个方向上研究含铝炸药在试验装置中爆炸后的水中冲击波压力的爆炸相似关系。选取JAL炸药在充装有1.0 MPa氮气的试验装置中的冲击波压力峰值pm与对比距离
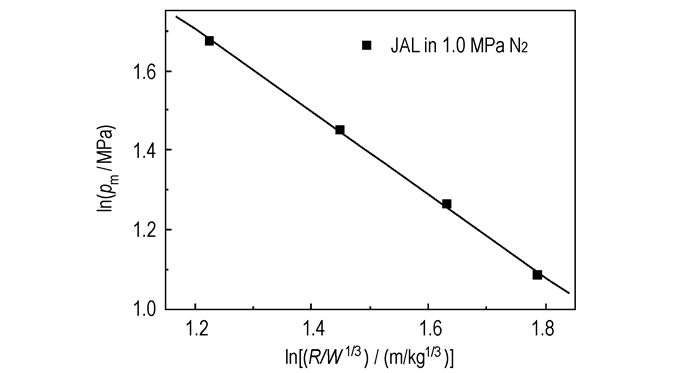
|
图 4 峰值压力与对比距离的关系 Fig.4 Relationship between peak pressure and contrastive distance |
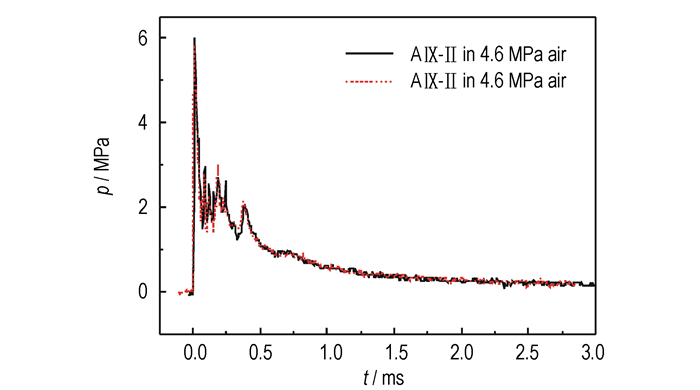
在对后燃效应进行研究时,选取距爆心2.5 m处的AⅨ-Ⅱ装药的实验数据进行比较。在不同的实验情况下均进行两发平行实验,图 5给出了AⅨ-Ⅱ在充有4.6 MPa空气的试验装置中进行的两发平行实验的冲击波压力时程曲线。从图 5中可以看出,实验平行性较好,总体而言,两发实验的误差小于5%。
|
图 5 两发平行实验的冲击波压力时程曲线对比 Fig.5 Comparison of pressure-time curves of two parallel experiments for AⅨ-Ⅱ |
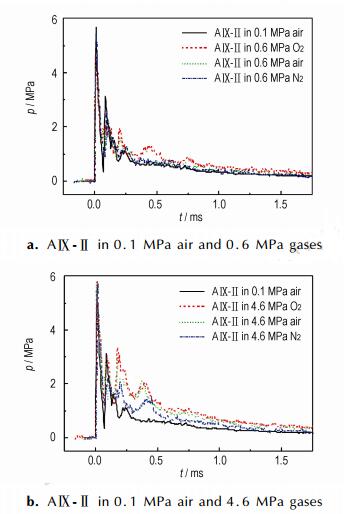
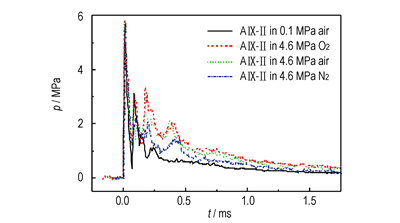
图 6给出了AⅨ-Ⅱ的冲击波压力时程曲线,图中分别将试验装置中充装有0.6 MPa和4.6 MPa的氧气、空气和氮气与0.1 MPa(常压)的空气情况下的冲击波压力时程曲线进行了对比。对于氧气和空气来说,由于压力和氧气浓度不同,试验装置中的氧气含量也不同。按照是否可将炸药(不考虑传爆药与雷管)中可燃元素完全氧化的原则,对于AⅨ-Ⅱ计算可知4.6 MPa氧气情况下氧气是富余的,而其余情况下氧气是不足的。
|
图 6 AⅨ-Ⅱ的冲击波压力时程曲线 Fig.6 The shock wave pressure-time curves of AⅨ-Ⅱ |
由图 6a可知,在冲击波波头到达0.2 ms之后,0.6 MPa氧气的冲击波压力最大,其次是0.6 MPa空气,而0.6 MPa氮气则与0.1 MPa空气的较接近且最小。由图 6b可知,在冲击波波头到达0.2 ms之后,4.6 MPa氧气的冲击波压力最大,而后从大到小依次是4.6 MPa空气、4.6 MPa氮气和0.1 MPa空气的曲线。
从压力时程曲线可以看出,充有氧气和空气的冲击波压力大于充有氮气的,这是由于氧气和空气中后燃效应的存在,显然充有相同压力氧气的冲击波压力会大于空气的。
4.4 后燃效应能量的计算按照第3节给出的计算方法,对两发平行实验的计算结果取平均值得到AⅨ-Ⅱ装药在不同情况下的水下爆炸实验结果,见表 2。
| 表 2 AⅨ-Ⅱ的水下爆炸实验结果 Tab.2 Experimental results of AⅨ-Ⅱ underwater explosion |
由表 2中数据可知,与0.6 MPa气体相比,4.6 MPa情况下相同气体的比冲击波能、比气泡能和总比能量均有大幅度提高,比冲击波能的提高主要是由于后燃效应的存在使冲击波压力曲线衰减变慢,而比气泡能能的提高除了由于后燃效应的存在,试验装置内的高压气体亦有贡献。
在装药被置于充有压力的气体的试验装置之后,根据能量守恒定律可以近似得到:
| $ \begin{array}{l} {\rm{裸药爆炸能量}}{\mathit{E}_1} + {\rm{后燃效应释放的能量}}{E_2} + {\rm{高压气体爆破能量}}{E_3} = \\ {\rm{冲击波能}}{E_4} + {\rm{气泡能}}{E_5} + {\rm{壳体破坏能}}{E_6} + {\rm{破片能}}{E_7} \end{array} $ | (12) |
为了求得后燃效应释放的能量E2,则必须知道其他六个能量值,而这其中的壳体破坏能E6和破片能E7随炸药性质变化且很难求得,故需采取其它方法来求得后燃效应释放的能量。
由于在实验条件下所用的含铝炸药不与氮气发生后燃反应[9],据此用某压力下氧气或空气的总能量减去相同压力下氮气的总能量,就得到了后燃效应释放的能量。由此计算出的AⅨ-Ⅱ后燃效应比能量和其与爆热的比值(以百分数值表示)列于表 3中。由表 3数据可以看出,在相同压力情况下,氧气中的后燃效应比空气中的强; 在相同气体情况下,4.6 MPa下的后燃效应比0.6 MPa下的强。在实验研究范围内,后燃效应释放的能量随着氧气含量增大而增大,最高值达到了爆热的78%,而根据理论计算,AⅨ-Ⅱ的后燃效应能量可以达到爆热的100%以上[1, 10]。
| 表 3 AⅨ-Ⅱ后燃效应释放的能量 Tab.3 Energy released by afterburning effect of AⅨ-Ⅱ |
(1) 使用水下爆炸测量炸药能量的方法,结合设计的双层容器试验装置,可以对含铝炸药的后燃效应进行测量,实验平行性较好,距爆源同一距离、同一水平但不同方位处的水下爆炸测试参数一致,在测试范围内冲击波超压峰值符合爆炸相似律。
(2) 从含铝炸药的超压时程曲线和后燃效应释放出的能量来看,该试验装置可明显增强含铝炸药的后燃效应。在实验研究范围内,后燃效应释放的能量随着氧气含量增大而增大,最高值达到了爆热的78%。
(3) 给出的计算炸药后燃效应能量的方法,可以为炸药的配方设计提供一定的参考。
致谢: 感谢南京理工大学化工学院安全工程系的刘荣海教授、饶国宁讲师以及黄磊、吴蒙、汪飞、周健美、孙欣等研究生在实验方案制定与实施等方面的帮助!| [1] |
孙业斌, 惠君明, 曹欣茂.
军用混合炸药[M]. 北京: 兵器工业出版社, 1995: 364-369, 467.
|
| [2] |
Volk F, Schedlbauer F. Analysis of post detonation products of different explosive charges[J].
Propellants, Explosives, Pyrotechnics, 1999, 24(3): 182-188. DOI:10.1002/(ISSN)1521-4087 |
| [3] |
Ornellas D L. Calorimetric determinations of the heat and products of detonation for explosives: October 1961 to April 1982. UCRL-52821[R], 1982.
|
| [4] |
苏华, 陈网桦, 吴涛, 等. 炸药水下爆炸冲击波参数的修正[J].
火炸药学报, 2004, 27(3): 46-48, 52. SU Hua, CHEN Wang-hua, WU Tao, et al. Amendment of shock wave parameters of underwater explosion[J]. Chinese Journal of Explosives and Propellants, 2004, 27(3): 46-48, 52. |
| [5] |
史锐, 徐更光, 刘德润, 等. 炸药爆炸能量的水中测试与分析[J].
火炸药学报, 2008, 31(4): 1-5. SHI Rui, XU Geng-guang, LIU De-run, et al. Underwater test and analysis for explosion energy of explosives[J]. Chinese Journal of Explosives and Propellants, 2008, 31(4): 1-5. |
| [6] |
孙华, 郭志军. 高能聚黑类传爆药在水中兵器中应用研究[J].
装备指挥技术学院学报, 2010, 21(3): 111-113. SUN Hua, GUO Zhi-jun. Study on the application of high energy hexogen booster in undersea weapons[J]. Journal of the Academy of Equipment Command & Technology, 2010, 21(3): 111-113. |
| [7] |
Bjarnholt G, Holmberg R. Explosive expansion waves in underwater detonation[C]//Proceedings of the 6th International Symposium on Detonation. San Diego, California, 1976: 540-550.
|
| [8] |
Bjarnholt G. 关于水下爆炸试验测量方法标准和数据计算标准的建议[C]//陈正衡译. 工业炸药测试新技术: 国际炸药测试方法标准化研究组织第八届会议论文集. 北京: 煤炭工业出版社, 1982: 88-105.
|
| [9] |
Kiciński W, Trzciński W A. Calorimetry studies of explosion heat of non-ideal explosives[J].
Journal of Thermal Analysis and Calorimetry, 2009, 96(2): 623-630. DOI:10.1007/s10973-008-9100-5 |
| [10] |
欧育湘.
炸药学[M]. 北京: 北京理工大学出版社, 2006: 200.
|
The afterburning effect of aluminized explosives was studied by underwater explosion method, and a double-layer test device designed for enhancing the afterburning effect of under-oxidized explosives was used.




